Estimating equations
Encyclopedia
In statistics, the method of estimating equations is a way of specifying how the parameters of a statistical model
should be estimated
. This can be thought of as a generalisation of many classical methods --- the method of moments
, least squares
, and maximum likelihood
--- as well as some recent methods like M-estimator
s.
The basis of the method is to have, or to find, a set of simultaneous equations involving both the sample data and the unknown model parameters which are to be solved in order to define the estimates of the parameters. Various components of the equations are defined in terms of the set of observed data on which the estimates are to be based.
Important examples of estimating equations are the likelihood equation
s.
which has the probability density function
:
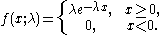
Suppose that a sample of data is available from which either the sample mean,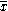
, or the sample median, m, can be calculated. Then an estimating equation based on the mean is
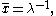
while the estimating equation based on the median is
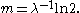
Each of these equations is derived by equating a sample value (sample statistic) to a theoretical (population) value. In each case the sample statistic is a consistent estimator
of the population value, and this provides an intuitive justification for this type of approach to estimation.
Statistical model
A statistical model is a formalization of relationships between variables in the form of mathematical equations. A statistical model describes how one or more random variables are related to one or more random variables. The model is statistical as the variables are not deterministically but...
should be estimated
Estimation
Estimation is the calculated approximation of a result which is usable even if input data may be incomplete or uncertain.In statistics,*estimation theory and estimator, for topics involving inferences about probability distributions...
. This can be thought of as a generalisation of many classical methods --- the method of moments
Method of moments
Method of moments may refer to:* Method of moments , a method of parameter estimation in statistics* Method of moments , a way of proving convergence in distribution in probability theory...
, least squares
Least squares
The method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
, and maximum likelihood
Maximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
--- as well as some recent methods like M-estimator
M-estimator
In statistics, M-estimators are a broad class of estimators, which are obtained as the minima of sums of functions of the data. Least-squares estimators and many maximum-likelihood estimators are M-estimators. The definition of M-estimators was motivated by robust statistics, which contributed new...
s.
The basis of the method is to have, or to find, a set of simultaneous equations involving both the sample data and the unknown model parameters which are to be solved in order to define the estimates of the parameters. Various components of the equations are defined in terms of the set of observed data on which the estimates are to be based.
Important examples of estimating equations are the likelihood equation
Maximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
s.
Examples
Consider the problem of estimating the rate parameter, λ of the exponential distributionExponential distribution
In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
which has the probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
:
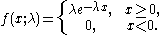
Suppose that a sample of data is available from which either the sample mean,
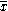, or the sample median, m, can be calculated. Then an estimating equation based on the mean is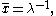while the estimating equation based on the median is
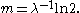
Each of these equations is derived by equating a sample value (sample statistic) to a theoretical (population) value. In each case the sample statistic is a consistent estimator
Consistent estimator
In statistics, a sequence of estimators for parameter θ0 is said to be consistent if this sequence converges in probability to θ0...
of the population value, and this provides an intuitive justification for this type of approach to estimation.
See also
- Generalized estimating equations
- Method of moments (statistics)
- Generalized method of momentsGeneralized method of momentsIn econometrics, generalized method of moments is a generic method for estimating parameters in statistical models. Usually it is applied in the context of semiparametric models, where the parameter of interest is finite-dimensional, whereas the full shape of the distribution function of the data...
- Maximum likelihoodMaximum likelihoodIn statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....