M-estimator
Encyclopedia
In statistics
, M-estimators are a broad class of estimator
s, which are obtained as the minima of sums of functions of the data. Least-squares estimators and many maximum-likelihood estimators are M-estimators. The definition of M-estimators was motivated by robust statistics
, which contributed new types of M-estimators. The statistical procedure of evaluating an M-estimator on a data set is called M-estimation.
More generally, an M-estimator may be defined to be a zero of an estimating function
. This estimating function is often the derivative of another statistical function: For example, a maximum-likelihood estimate is often defined to be a zero of the derivative of the likelihood function with respect the parameter: thus, a maximum-likelihood estimator is often a critical point
of the score
function. In many applications, such M-estimators can be thought of as estimating characteristics of the population.
Another popular M-estimator is maximum-likelihood estimation. For a family of probability density function
s f parameterized by θ, a maximum likelihood
estimator of θ is computed for each set of data by maximizing the likelihood function
over the parameter space { θ } . When the observations are independent and identically distributed, a ML-estimate
satisfies
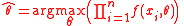
or, equivalently,
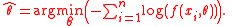
Maximum-likelihood estimators are often inefficient and biased for finite samples. For many regular problems, maximum-likelihood estimation performs well for "large samples", being an approximation of a posterior mode. If the problem is "regular", then any bias of the MLE (or posterior mode) decreases to zero when the sample-size increases to infinity. The performance of maximum-likelihood (and posterior-mode) estimators drops when the parametric family is mis-specified.
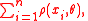
where ρ is a function with certain properties (see below). The solutions
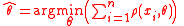
are called M-estimators ("M" for "maximum likelihood-type" (Huber, 1981, page 43)); other types of robust estimator include L-estimators, R-estimators and S-estimators. Maximum likelihood estimators are thus a special case of M-estimators. With suitable rescaling, M-estimators are special cases of extremum estimator
s (in which more general functions of the observations can be used).
The function ρ, or its derivative, ψ, can be chosen in such a way to provide the estimator desirable properties (in terms of bias and efficiency) when the data are truly from the assumed distribution, and 'not bad' behaviour when the data are generated from a model that is, in some sense, close to the assumed distribution.
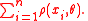
This minimization can always be done directly. Often it is simpler to differentiate with respect to θ and solve for the root of the derivative. When this differentiation is possible, the M-estimator is said to be of ψ-type. Otherwise, the M-estimator is said to be of ρ-type.
In most practical cases, the M-estimators are of ψ-type.
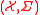and 
be measure spaces.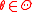 
is a vector of parameters. An M-estimator of ρ-type T is defined through a measurable function 
. It maps a probability distribution F on 
to the value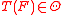 
(if it exists) that minimizes
:
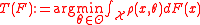
For example, for the maximum likelihood
estimator,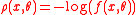
, where 
.
is differentiable, the computation of 
is usually much easier. An M-estimator of ψ-type T is defined through a measurable function 
. It maps a probability distribution F on 
to the value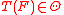 
(if it exists) that solves the vector equation:
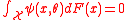
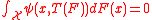
For example, for the maximum likelihood
estimator,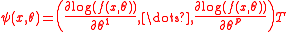
, where 
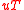denotes the transpose of vector u and 
.
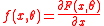Such an estimator is not necessarily an M-estimator of ρ-type, but if ρ has a continuous first derivative with respect to
, then a necessary corresponding M-estimator of ψ-type to be an M-estimator of ρ-type is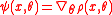 
. The previous definitions can easily be extended to finite samples.
If the function ψ decreases to zero as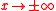
, the estimator is called redescending
. Such estimators have some additional desirable properties, such as complete rejection of gross outliers.
fitting algorithm can be performed; this is typically the preferred method.
For some choices of ψ, specifically, redescending
functions, the solution may not be unique. The issue is particularly relevant in multivariate and regression problems. Thus, some care is needed to ensure that good starting points are chosen. Robust
starting points, such as the median
as an estimate of location and the median absolute deviation
as a univariate estimate of scale, are common.
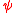-type is proportional to its defining 
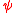function.
Let T be an M-estimator of ψ-type, and G be a probability distribution for which
is defined. Its influence function IF is
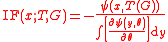
A proof of this property of M-estimators can be found in Huber (1981, Section 3.2).
If we define
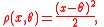
we note that this is minimized when θ is the mean
of the Xs. Thus the mean is an M-estimator of ρ-type, with this ρ function.
As this ρ function is continuously differentiable in θ, the mean is thus also an M-estimator of ψ-type for ψ(x, θ) = θ - x.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, M-estimators are a broad class of estimator
Estimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
s, which are obtained as the minima of sums of functions of the data. Least-squares estimators and many maximum-likelihood estimators are M-estimators. The definition of M-estimators was motivated by robust statistics
Robust statistics
Robust statistics provides an alternative approach to classical statistical methods. The motivation is to produce estimators that are not unduly affected by small departures from model assumptions.- Introduction :...
, which contributed new types of M-estimators. The statistical procedure of evaluating an M-estimator on a data set is called M-estimation.
More generally, an M-estimator may be defined to be a zero of an estimating function
Estimating equations
In statistics, the method of estimating equations is a way of specifying how the parameters of a statistical model should be estimated. This can be thought of as a generalisation of many classical methods --- the method of moments, least squares, and maximum likelihood --- as well as some recent...
. This estimating function is often the derivative of another statistical function: For example, a maximum-likelihood estimate is often defined to be a zero of the derivative of the likelihood function with respect the parameter: thus, a maximum-likelihood estimator is often a critical point
Critical point
Critical point may refer to:*Critical point *Critical point *Critical point *Construction point of a ski jumping hill-See also:*Brillouin zone*Percolation thresholds...
of the score
Score (statistics)
In statistics, the score, score function, efficient score or informant plays an important role in several aspects of inference...
function. In many applications, such M-estimators can be thought of as estimating characteristics of the population.
Historical motivation
The method of least squares is a prototypical M-estimator, since the estimator is defined as a minimum of the sum of squares of the residuals.Another popular M-estimator is maximum-likelihood estimation. For a family of probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
s f parameterized by θ, a maximum likelihood
Maximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
estimator of θ is computed for each set of data by maximizing the likelihood function
Likelihood function
In statistics, a likelihood function is a function of the parameters of a statistical model, defined as follows: the likelihood of a set of parameter values given some observed outcomes is equal to the probability of those observed outcomes given those parameter values...
over the parameter space { θ } . When the observations are independent and identically distributed, a ML-estimate
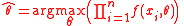
satisfiesor, equivalently,
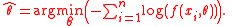
Maximum-likelihood estimators are often inefficient and biased for finite samples. For many regular problems, maximum-likelihood estimation performs well for "large samples", being an approximation of a posterior mode. If the problem is "regular", then any bias of the MLE (or posterior mode) decreases to zero when the sample-size increases to infinity. The performance of maximum-likelihood (and posterior-mode) estimators drops when the parametric family is mis-specified.
Definition
In 1964, Peter Huber proposed generalizing maximum likelihood estimation to the minimization of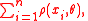where ρ is a function with certain properties (see below). The solutions
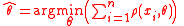
are called M-estimators ("M" for "maximum likelihood-type" (Huber, 1981, page 43)); other types of robust estimator include L-estimators, R-estimators and S-estimators. Maximum likelihood estimators are thus a special case of M-estimators. With suitable rescaling, M-estimators are special cases of extremum estimator
Extremum estimator
In statistics and econometrics, extremum estimators is a wide class of estimators for parametric models that are calculated through maximization of a certain objective function, which depends on the data...
s (in which more general functions of the observations can be used).
The function ρ, or its derivative, ψ, can be chosen in such a way to provide the estimator desirable properties (in terms of bias and efficiency) when the data are truly from the assumed distribution, and 'not bad' behaviour when the data are generated from a model that is, in some sense, close to the assumed distribution.
Types of M-estimators
M-estimators are solutions, θ, which minimize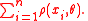This minimization can always be done directly. Often it is simpler to differentiate with respect to θ and solve for the root of the derivative. When this differentiation is possible, the M-estimator is said to be of ψ-type. Otherwise, the M-estimator is said to be of ρ-type.
In most practical cases, the M-estimators are of ψ-type.
ρ-type
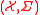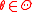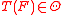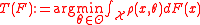
For positive integer r, let and be measure spaces. is a vector of parameters. An M-estimator of ρ-type T is defined through a measurable function . It maps a probability distribution F on to the value (if it exists) that minimizes:For example, for the maximum likelihood
Maximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
estimator,
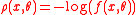, where .ψ-type
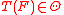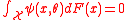
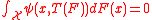
If is differentiable, the computation of is usually much easier. An M-estimator of ψ-type T is defined through a measurable function . It maps a probability distribution F on to the value (if it exists) that solves the vector equation:For example, for the maximum likelihood
Maximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
estimator,
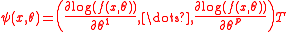, where 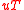denotes the transpose of vector u and 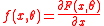.Such an estimator is not necessarily an M-estimator of ρ-type, but if ρ has a continuous first derivative with respect to
, then a necessary corresponding M-estimator of ψ-type to be an M-estimator of ρ-type is 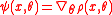. The previous definitions can easily be extended to finite samples.If the function ψ decreases to zero as
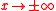, the estimator is called redescendingRedescending M-estimator
In statistics, Redescending M-estimators are Ψ-type M-estimators which have Ψ functions that are non-decreasing near the origin, but decreasing toward 0 far from the origin...
. Such estimators have some additional desirable properties, such as complete rejection of gross outliers.
Computation
For many choices of ρ or ψ, no closed form solution exists and an iterative approach to computation is required. It is possible to use standard function optimization algorithms, such as Newton-Raphson. However, in most cases an iteratively re-weighted least squaresIteratively re-weighted least squares
The method of iteratively reweighted least squares is used to solve certain optimization problems. It solves objective functions of the form:...
fitting algorithm can be performed; this is typically the preferred method.
For some choices of ψ, specifically, redescending
Redescending M-estimator
In statistics, Redescending M-estimators are Ψ-type M-estimators which have Ψ functions that are non-decreasing near the origin, but decreasing toward 0 far from the origin...
functions, the solution may not be unique. The issue is particularly relevant in multivariate and regression problems. Thus, some care is needed to ensure that good starting points are chosen. Robust
Robust statistics
Robust statistics provides an alternative approach to classical statistical methods. The motivation is to produce estimators that are not unduly affected by small departures from model assumptions.- Introduction :...
starting points, such as the median
Median
In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
as an estimate of location and the median absolute deviation
Median absolute deviation
In statistics, the median absolute deviation is a robust measure of the variability of a univariate sample of quantitative data. It can also refer to the population parameter that is estimated by the MAD calculated from a sample....
as a univariate estimate of scale, are common.
Distribution
It can be shown that M-estimators are asymptotically normally distributed. As such, Wald-type approaches to constructing confidence intervals and hypothesis tests can be used. However, since the theory is asymptotic, it will frequently be sensible to check the distribution, perhaps by examining the permutation or bootstrap distribution.Influence function
The influence function of an M-estimator of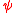-type is proportional to its defining 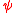function.Let T be an M-estimator of ψ-type, and G be a probability distribution for which
is defined. Its influence function IF is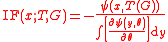A proof of this property of M-estimators can be found in Huber (1981, Section 3.2).
Applications
M-estimators can be constructed for location parameters and scale parameters in univariate and multivariate settings, as well as being used in robust regression .Mean
Let (X1, ..., Xn) be a set of independent, identically distributed random variables, with distribution F.If we define
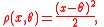
we note that this is minimized when θ is the mean
Arithmetic mean
In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
of the Xs. Thus the mean is an M-estimator of ρ-type, with this ρ function.
As this ρ function is continuously differentiable in θ, the mean is thus also an M-estimator of ψ-type for ψ(x, θ) = θ - x.
External links
- M-estimators — an introduction to the subject by Zhengyou Zhang