Median absolute deviation
Encyclopedia
In statistics
, the median absolute deviation (MAD) is a robust
measure of the variability
of a univariate
sample of quantitative data. It can also refer to the population
parameter
that is estimated by the MAD calculated from a sample.
For a univariate data set X1, X2, ..., Xn, the MAD is defined as the median
of the absolute deviation
s from the data's median:
that is, starting with the residuals
(deviations) from the data's median, the MAD is the median
of their absolute values.
. It is a more robust estimator of scale than the sample variance
or standard deviation
. It thus behaves better with distributions without a mean or variance, such as the Cauchy distribution
.
For instance, the MAD is a robust statistic, being more resilient to outliers in a data set than the standard deviation. In the standard deviation, the distances from the mean
are squared, so on average, large deviations are weighted more heavily, and thus outliers can heavily influence it. In the MAD, the magnitude of the distances of a small number of outliers is irrelevant.
for the
estimation of the standard deviation
σ, one takes
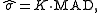
where K is a constant scale factor
, which depends on the distribution.
For normally distributed data K is taken to be 1/Φ−1(3/4)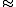
1.4826, where Φ−1 is the inverse of the cumulative distribution function
for the standard normal distribution, i.e., the quantile function
. This is because the MAD is given by:
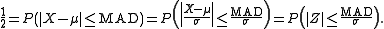
Therefore we must have that Φ(MAD/σ) − Φ(−MAD/σ) = 1/2. Since Φ(−MAD/σ) = 1 − Φ(MAD/σ) we have that MAD/σ = Φ−1(3/4) from which we obtain the scale factor K = 1/Φ−1(3/4).
Hence
In other words, the expectation of 1.4826 times the MAD for large samples of normally distributed Xi is approximately equal to the population standard deviation. Other distributions behave differently: for example for large samples from a uniform continuous distribution, this factor is about 1.1547 (the square root of 4/3).
rather than on a sample. For a symmetric distribution with zero mean, the population MAD is the 75th percentile
of the distribution.
Unlike the variance, which may be infinite or undefined, the population MAD is always a finite number. For example, the standard Cauchy distribution
has undefined variance, but its MAD is 1.
The earliest known mention of the concept of the MAD occurred in 1816, in a paper by Carl Friedrich Gauss
on the determination of the accuracy of numerical observations.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the median absolute deviation (MAD) is a robust
Robust statistics
Robust statistics provides an alternative approach to classical statistical methods. The motivation is to produce estimators that are not unduly affected by small departures from model assumptions.- Introduction :...
measure of the variability
Statistical dispersion
In statistics, statistical dispersion is variability or spread in a variable or a probability distribution...
of a univariate
Univariate
In mathematics, univariate refers to an expression, equation, function or polynomial of only one variable. Objects of any of these types but involving more than one variable may be called multivariate...
sample of quantitative data. It can also refer to the population
Statistical population
A statistical population is a set of entities concerning which statistical inferences are to be drawn, often based on a random sample taken from the population. For example, if we were interested in generalizations about crows, then we would describe the set of crows that is of interest...
parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
that is estimated by the MAD calculated from a sample.
For a univariate data set X1, X2, ..., Xn, the MAD is defined as the median
Median
In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
of the absolute deviation
Absolute deviation
In statistics, the absolute deviation of an element of a data set is the absolute difference between that element and a given point. Typically the point from which the deviation is measured is a measure of central tendency, most often the median or sometimes the mean of the data set.D_i = |x_i-m|...
s from the data's median:
that is, starting with the residuals
Errors and residuals in statistics
In statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...
(deviations) from the data's median, the MAD is the median
Median
In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
of their absolute values.
Example
Consider the data (1, 1, 2, 2, 4, 6, 9). It has a median value of 2. The absolute deviations about 2 are (1, 1, 0, 0, 2, 4, 7) which in turn have a median value of 1 (because the sorted absolute deviations are (0, 0, 1, 1, 2, 4, 7)). So the median absolute deviation for this data is 1.Uses
The median absolute deviation is a measure of statistical dispersionStatistical dispersion
In statistics, statistical dispersion is variability or spread in a variable or a probability distribution...
. It is a more robust estimator of scale than the sample variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
or standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
. It thus behaves better with distributions without a mean or variance, such as the Cauchy distribution
Cauchy distribution
The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
.
For instance, the MAD is a robust statistic, being more resilient to outliers in a data set than the standard deviation. In the standard deviation, the distances from the mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
are squared, so on average, large deviations are weighted more heavily, and thus outliers can heavily influence it. In the MAD, the magnitude of the distances of a small number of outliers is irrelevant.
Relation to standard deviation
In order to use the MAD as a consistent estimatorConsistent estimator
In statistics, a sequence of estimators for parameter θ0 is said to be consistent if this sequence converges in probability to θ0...
for the
estimation of the standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
σ, one takes
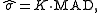
where K is a constant scale factor
Scale factor
A scale factor is a number which scales, or multiplies, some quantity. In the equation y=Cx, C is the scale factor for x. C is also the coefficient of x, and may be called the constant of proportionality of y to x...
, which depends on the distribution.
For normally distributed data K is taken to be 1/Φ−1(3/4)
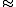1.4826, where Φ−1 is the inverse of the cumulative distribution functionCumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
for the standard normal distribution, i.e., the quantile function
Quantile function
In probability and statistics, the quantile function of the probability distribution of a random variable specifies, for a given probability, the value which the random variable will be at, or below, with that probability...
. This is because the MAD is given by:
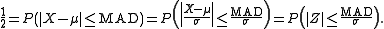
Therefore we must have that Φ(MAD/σ) − Φ(−MAD/σ) = 1/2. Since Φ(−MAD/σ) = 1 − Φ(MAD/σ) we have that MAD/σ = Φ−1(3/4) from which we obtain the scale factor K = 1/Φ−1(3/4).
Hence
In other words, the expectation of 1.4826 times the MAD for large samples of normally distributed Xi is approximately equal to the population standard deviation. Other distributions behave differently: for example for large samples from a uniform continuous distribution, this factor is about 1.1547 (the square root of 4/3).
The population MAD
The population MAD is defined analogously to the sample MAD, but is based on the complete distributionProbability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
rather than on a sample. For a symmetric distribution with zero mean, the population MAD is the 75th percentile
Percentile
In statistics, a percentile is the value of a variable below which a certain percent of observations fall. For example, the 20th percentile is the value below which 20 percent of the observations may be found...
of the distribution.
Unlike the variance, which may be infinite or undefined, the population MAD is always a finite number. For example, the standard Cauchy distribution
Cauchy distribution
The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
has undefined variance, but its MAD is 1.
The earliest known mention of the concept of the MAD occurred in 1816, in a paper by Carl Friedrich Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
on the determination of the accuracy of numerical observations.