Quantile function
Encyclopedia
In probability
and statistics
, the quantile function of the probability distribution
of a random variable
specifies, for a given probability, the value which the random variable will be at, or below, with that probability. The quantile function is one way of prescribing a probability distribution, and it is an alternative to the probability density
or mass function
, the cumulative distribution function
and the characteristic function
. The quantile function, Q, of a probability distribution
is the inverse
of its cumulative distribution function
(cdf) F. The derivative of the quantile function, namely the
quantile density function, is yet another way of prescribing a probability distribution. It is the reciprocal of the pdf composed
with the quantile function.
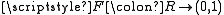, the quantile function returns the value below which random draws from the given distribution would fall, p×100 percent of the time. That is, it returns the value of x such that
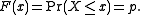
If the probability distribution is discrete rather than continuous then there may be gaps between values in the domain of its cdf,
while if the cdf is only weakly monotonic there may be "flat spots" in its range. In either case, the quantile function is
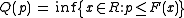
for a probability 0 < p < 1, and the quantile function returns the minimum value of x for which the previous probability statement holds.
1/λ) is
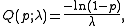
for 0 ≤ p < 1. The quartile
s are therefore:
first quartile :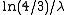
median
:
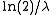
third quartile :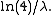
s.
For statistical applications, users need to know key percentage points of a given distribution. For example, they require the median and 25% and 75% quartiles as in the example above or 5%, 95%, 2.5%, 97.5% levels for other applications such as assessing the statistical significance
of an observation whose distribution is known; see the quantile
entry. Statistical applications of quantile functions are discussed extensively by Gilchrist.
Monte-Carlo simulations employ quantile functions to produce non-uniform random or pseudorandom numbers for use in diverse types of simulation calculations. A sample from a given distribution may be obtained in principle by applying its quantile function to a sample from a uniform distribution. The demands, for example, of simulation methods in modern computational finance
are focusing increasing attention on methods based on quantile functions, as they work well with multivariate techniques based on either copula
or quasi-Monte-Carlo methods and Monte Carlo methods in finance
.
can be found (others include the uniform
, the Weibull, the Tukey lambda (which includes the logistic
) and the log-logistic
). When the cdf itself has a closed-form expression, one can always use a numerical root-finding algorithm
such as the bisection method
to invert the cdf. Other algorithms to evaluate quantile functions are given in the Numerical Recipes
series of books. Algorithms for common distributions are built in to many statistical software packages.
Quantile functions may also be characterized as solutions of non-linear ordinary and partial differential equation
s. The ordinary differential equation
s for the cases of the normal, Student, beta and gamma distributions have been given and solved.
function. Non-composite rational approximations have been developed by Shaw (see Monte Carlo recycling in External Links).
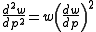
with the centre (boundary) conditions
This equation may be solved by several methods, including the classical power series approach. From this solutions of arbitrarily high accuracy may be developed (see Steinbrecher and Shaw, 2008).
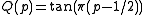
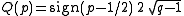
where
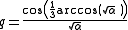
and
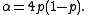
In the above the "sign" function is +1 for positive arguments, -1 for negative arguments and zero at zero. It should not be confused with the trigonometric sine function.
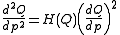
augmented by suitable boundary conditions, where
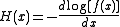
and ƒ(x) is the probability density function. The forms of this equation, and its classical analysis by series and asymptotic solutions, for the cases of the normal, Student, gamma and beta distributions has been elucidated by Steinbrecher and Shaw (2008). Such solutions provide accurate benchmarks, and in the case of the Student, suitable series for live Monte Carlo use.
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the quantile function of the probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
specifies, for a given probability, the value which the random variable will be at, or below, with that probability. The quantile function is one way of prescribing a probability distribution, and it is an alternative to the probability density
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
or mass function
Probability mass function
In probability theory and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value...
, the cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
and the characteristic function
Characteristic function (probability theory)
In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
. The quantile function, Q, of a probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
is the inverse
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
of its cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
(cdf) F. The derivative of the quantile function, namely the
quantile density function, is yet another way of prescribing a probability distribution. It is the reciprocal of the pdf composed
with the quantile function.
Definition
Assuming a continuous and strictly monotonic distribution function,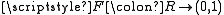, the quantile function returns the value below which random draws from the given distribution would fall, p×100 percent of the time. That is, it returns the value of x such that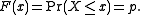If the probability distribution is discrete rather than continuous then there may be gaps between values in the domain of its cdf,
while if the cdf is only weakly monotonic there may be "flat spots" in its range. In either case, the quantile function is
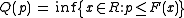
for a probability 0 < p < 1, and the quantile function returns the minimum value of x for which the previous probability statement holds.
Simple example
For example, the quantile function for Exponential(λ) (i.e. intensity λ and expected valueExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
1/λ) is
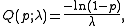
for 0 ≤ p < 1. The quartile
Quartile
In descriptive statistics, the quartiles of a set of values are the three points that divide the data set into four equal groups, each representing a fourth of the population being sampled...
s are therefore:
first quartile :
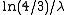
median
Median
In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
:
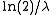
third quartile :
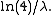
Applications
Quantile functions are used in both statistical applications and Monte Carlo methodMonte Carlo method
Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
s.
For statistical applications, users need to know key percentage points of a given distribution. For example, they require the median and 25% and 75% quartiles as in the example above or 5%, 95%, 2.5%, 97.5% levels for other applications such as assessing the statistical significance
Statistical significance
In statistics, a result is called statistically significant if it is unlikely to have occurred by chance. The phrase test of significance was coined by Ronald Fisher....
of an observation whose distribution is known; see the quantile
Quantile
Quantiles are points taken at regular intervals from the cumulative distribution function of a random variable. Dividing ordered data into q essentially equal-sized data subsets is the motivation for q-quantiles; the quantiles are the data values marking the boundaries between consecutive subsets...
entry. Statistical applications of quantile functions are discussed extensively by Gilchrist.
Monte-Carlo simulations employ quantile functions to produce non-uniform random or pseudorandom numbers for use in diverse types of simulation calculations. A sample from a given distribution may be obtained in principle by applying its quantile function to a sample from a uniform distribution. The demands, for example, of simulation methods in modern computational finance
Computational finance
Computational finance, also called financial engineering, is a cross-disciplinary field which relies on computational intelligence, mathematical finance, numerical methods and computer simulations to make trading, hedging and investment decisions, as well as facilitating the risk management of...
are focusing increasing attention on methods based on quantile functions, as they work well with multivariate techniques based on either copula
Copula (statistics)
In probability theory and statistics, a copula can be used to describe the dependence between random variables. Copulas derive their name from linguistics....
or quasi-Monte-Carlo methods and Monte Carlo methods in finance
Monte Carlo methods in finance
Monte Carlo methods are used in finance and mathematical finance to value and analyze instruments, portfolios and investments by simulating the various sources of uncertainty affecting their value, and then determining their average value over the range of resultant outcomes. This is usually done...
.
Calculation
The evaluation of quantile functions often involves numerical methods, as the example of the exponential distribution above is one of the few distributions where a closed-form expressionClosed-form expression
In mathematics, an expression is said to be a closed-form expression if it can be expressed analytically in terms of a bounded number of certain "well-known" functions...
can be found (others include the uniform
Uniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
, the Weibull, the Tukey lambda (which includes the logistic
Logistic
Logistic may refer to:* Logistics, the management of resources and their distributions** Logistic engineering, the scientific study of logistics** Military logistics, the study of logistics at the service of military units and operations...
) and the log-logistic
Log-logistic distribution
In probability and statistics, the log-logistic distribution is a continuous probability distribution for a non-negative random variable. It is used in survival analysis as a parametric model for events whose rate increases initially and decreases later, for example mortality from cancer following...
). When the cdf itself has a closed-form expression, one can always use a numerical root-finding algorithm
Root-finding algorithm
A root-finding algorithm is a numerical method, or algorithm, for finding a value x such that f = 0, for a given function f. Such an x is called a root of the function f....
such as the bisection method
Bisection method
The bisection method in mathematics is a root-finding method which repeatedly bisects an interval and then selects a subinterval in which a root must lie for further processing. It is a very simple and robust method, but it is also relatively slow...
to invert the cdf. Other algorithms to evaluate quantile functions are given in the Numerical Recipes
Numerical Recipes
Numerical Recipes is the generic title of a series of books on algorithms and numerical analysis by William H. Press, Saul Teukolsky, William Vetterling and Brian Flannery. In various editions, the books have been in print since 1986...
series of books. Algorithms for common distributions are built in to many statistical software packages.
Quantile functions may also be characterized as solutions of non-linear ordinary and partial differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s. The ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s for the cases of the normal, Student, beta and gamma distributions have been given and solved.
The normal distribution
The normal distribution is perhaps the most important case, and, in the absence of a simple formula, approximate representations are usually used. Thorough composite rational and polynomial approximations have been given by Wichura and Acklam (see his web site in External Links). Also see the entry on the probitProbit
In probability theory and statistics, the probit function is the inverse cumulative distribution function , or quantile function associated with the standard normal distribution...
function. Non-composite rational approximations have been developed by Shaw (see Monte Carlo recycling in External Links).
Ordinary differential equation for the normal quantile
A non-linear ordinary differential equation for the normal quantile, w(p), may be given. It is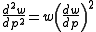with the centre (boundary) conditions
This equation may be solved by several methods, including the classical power series approach. From this solutions of arbitrarily high accuracy may be developed (see Steinbrecher and Shaw, 2008).
The Student's t-distribution
This has historically been one of the more intractable cases, as the presence of a parameter, ν, the degrees of freedom, makes the use of rational and other approximations awkward. Simple formulas exist when the ν = 1, 2, 4 and the problem may be reduced to the solution of a polynomial when ν is even. In other cases the quantile functions may be developed as power series. The simple cases are as follows:ν = 1 (Cauchy distribution)
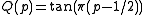
ν = 4
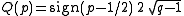
where
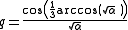
and
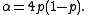
In the above the "sign" function is +1 for positive arguments, -1 for negative arguments and zero at zero. It should not be confused with the trigonometric sine function.
Non-linear differential equations for quantile functions
The non-linear ordinary differential equation given for normal distribution is a special case of that available for any quantile function whose second derivative exists. In general the equation for a quantile, Q(p), may be given. It is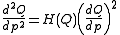augmented by suitable boundary conditions, where
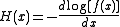
and ƒ(x) is the probability density function. The forms of this equation, and its classical analysis by series and asymptotic solutions, for the cases of the normal, Student, gamma and beta distributions has been elucidated by Steinbrecher and Shaw (2008). Such solutions provide accurate benchmarks, and in the case of the Student, suitable series for live Monte Carlo use.