Monte Carlo methods in finance
Encyclopedia
Monte Carlo method
s are used in finance
and mathematical finance
to value and analyze (complex) instruments, portfolio
s and investment
s by simulating
the various sources of uncertainty affecting their value, and then determining their average value over the range of resultant outcomes. This is usually done by help of stochastic asset models. The advantage of Monte Carlo methods over other techniques increases as the dimensions (sources of uncertainty) of the problem increase.
Monte Carlo methods were first introduced to finance in 1964 by David B. Hertz
through his Harvard Business Review
article, discussing their application in Corporate Finance
. In 1977, Phelim Boyle
pioneered the use of simulation in derivative valuation
in his seminal Journal of Financial Economics
paper.
This article discusses typical financial problems in which Monte Carlo methods are used. It also touches on the use of so-called "quasi-random" methods such as the use of Sobol sequence
s.
, chemistry
, computer science
etc.
In finance
, the Monte Carlo method is used to simulate the various sources of uncertainty that affect the value of the instrument, portfolio
or investment
in question, and to then calculate a representative value given these possible values of the underlying inputs. In terms of financial theory
, this, essentially, is an application of risk neutral valuation; see also risk neutrality.
Some examples:
Although Monte Carlo methods provide flexibility, and can handle multiple sources of uncertainty, the use of these techniques is nevertheless not always appropriate. In general, simulation methods are preferred to other valuation techniques only when there are several state variables (i.e. several sources of uncertainty). These techniques are also of limited use in valuing American style derivatives. See below.
entail the computation of a particular integral
(for instance the problem of finding the arbitrage-free value of a particular derivative
). In many cases these integrals can be valued analytically, and in still more cases they can be valued using numerical integration
, or computed using a partial differential equation
(PDE). However when the number of dimensions (or degrees of freedom) in the problem is large, PDEs and numerical integrals become intractable, and in these cases Monte Carlo method
s often give better results.
For more than three or four state variables, formulae such as Black Scholes (i.e. analytic solutions) do not exist, while other numerical methods such as the Binomial options pricing model
and finite difference method
s face several difficulties and are not practical. In these cases, Monte Carlo methods converge to the solution more quickly than numerical methods, require less memory and are easier to program. For simpler situations, however, simulation is not the better solution because it is very time-consuming and computationally intensive.
Monte Carlo methods can deal with derivatives which have path dependent payoffs in a fairly straight forward manner. On the other hand Finite Difference (PDE) solvers struggle with path dependence.
s. This is because, in contrast to a partial differential equation
, the Monte Carlo method really only estimates the option value assuming a given starting point and time.
However, for early exercise, we would also need to know the option value at the intermediate times between the simulation start time and the option expiry time. In the Black–Scholes PDE approach these prices are easily obtained, because the simulation runs backwards from the expiry date. In Monte-Carlo this information is harder to obtain, but it can be done for example using the least squares
algorithm of Carriere (see link to original paper) which was made popular a few years later by Longstaff and Schwartz (see link to original paper).
Stochastic Grid Method (SGM) proposed by Jain and Oosterlee provides a general framework for pricing high dimensional American options (see link to original paper).
states that the value of a derivative is equal to the discounted expected value of the derivative payoff where the expectation
is taken under the risk-neutral measure
[1]. An expectation is, in the language of pure mathematics
, simply an integral with respect to the measure. Monte Carlo methods are ideally suited to evaluating difficult integrals (see also Monte Carlo method
).
Thus if we suppose that our risk-neutral probability space is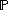
and that we have a derivative H that depends on a set of underlying instruments 
. Then given a sample 
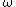from the probability space the value of the derivative is 
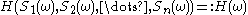. Today's value of the derivative is found by taking the expectation over all possible samples and discounting at the risk-free rate. I.e. the derivative has value:
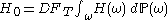
where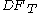
is the discount factor corresponding to the risk-free rate to the final maturity date T years into the future.
Now suppose the integral is hard to compute. We can approximate the integral by generating sample paths and then taking an average. Suppose we generate N samples then
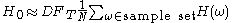
which is much easier to compute.
2. For example in the standard Black–Scholes model, the stock price evolves as
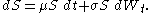
To sample a path following this distribution from time 0 to T, we chop the time interval into M units of length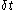
, and approximate the Brownian motion over the interval 
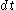by a single normal variable of mean 0 and variance 
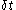. This leads to a sample path of
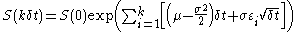
for each k between 1 and M. Here each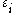
is a draw from a standard normal distribution.
Let us suppose that a derivative H pays the average value of S between 0 and T then a sample path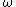
corresponds to a set 
and
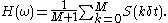
We obtain the Monte-Carlo value of this derivative by generating N lots of M normal variables, creating N sample paths and so N values of H, and then taking the average.
Commonly the derivative will depend on two or more (possibly correlated) underlyings. The method here can be extended to generate sample paths of several variables, where the normal variables building up the sample paths are appropriately correlated.
It follows from the central limit theorem
that quadrupling the number of sample paths approximately halves the error in the simulated price (i.e. the error has order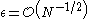
convergence in the sense of standard deviation of the solution).
In practice Monte Carlo methods are used for European-style derivatives involving at least three variables (more direct methods involving numerical integration can usually be used for those problems with only one or two underlyings. See Monte Carlo option model
.
This state of affairs can be mitigated by variance reduction
techniques.
to also take 
. Not only does this reduce the number of normal samples to be taken to generate N paths, but also, under same conditions, reduces the variance of the sample paths, improving the accuracy.
. Let us suppose that we wish to obtain the Monte Carlo value of a derivative H, but know the value analytically of a similar derivative I. Then H* = (Value of H according to Monte Carlo) + B*[(Value of I analytically) − (Value of I according to same Monte Carlo paths)] is a better estimate, where B is covar(H,I)/var(H).
The intuition behind that technique, when applied to derivatives, is the following: note that the source of the variance of a derivative will be directly dependent on the risks (e.g. delta, vega) of this derivative. This is because any error on, say, the estimator for the forward value of an underlier, will generate a corresponding error depending on the delta of the derivative with respect to this forward value. The simplest example to demonstrate this consists in comparing the error when pricing an at-the-money call and an at-the-money straddle (i.e. call+put), which has a much lower delta.
Therefore, a standard way of choosing the derivative I consists in choosing a replicating portfolio
s of options for H. In practice, one will price H without variance reduction, calculate deltas and vegas, and then use a combination of calls and puts that have the same deltas and vegas as control variate.
This technique can be particularly useful when calculating risks on a derivative. When calculating the delta using a Monte Carlo method, the most straightforward way is the black-box technique consisting in doing a Monte Carlo on the original market data and another one on the changed market data, and calculate the risk by doing the difference. Instead, the importance sampling method consists in doing a Monte Carlo in an arbitrary reference market data (ideally one in which the variance is as low as possible), and calculate the prices using the weight-changing technique described above. This results in a risk that will be much more stable than the one obtained through the black-box approach.
such as a Sobol sequence
. Taking averages of derivative payoffs at points in a low-discrepancy sequence is often more efficient than taking averages of payoffs at random points.
Derivative valuation
Corporate Finance
Value at Risk and portfolio analysis
Personal finance
Monte Carlo method
Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
s are used in finance
Finance
"Finance" is often defined simply as the management of money or “funds” management Modern finance, however, is a family of business activity that includes the origination, marketing, and management of cash and money surrogates through a variety of capital accounts, instruments, and markets created...
and mathematical finance
Mathematical finance
Mathematical finance is a field of applied mathematics, concerned with financial markets. The subject has a close relationship with the discipline of financial economics, which is concerned with much of the underlying theory. Generally, mathematical finance will derive and extend the mathematical...
to value and analyze (complex) instruments, portfolio
Portfolio (finance)
Portfolio is a financial term denoting a collection of investments held by an investment company, hedge fund, financial institution or individual.-Definition:The term portfolio refers to any collection of financial assets such as stocks, bonds and cash...
s and investment
Investment
Investment has different meanings in finance and economics. Finance investment is putting money into something with the expectation of gain, that upon thorough analysis, has a high degree of security for the principal amount, as well as security of return, within an expected period of time...
s by simulating
Simulation
Simulation is the imitation of some real thing available, state of affairs, or process. The act of simulating something generally entails representing certain key characteristics or behaviours of a selected physical or abstract system....
the various sources of uncertainty affecting their value, and then determining their average value over the range of resultant outcomes. This is usually done by help of stochastic asset models. The advantage of Monte Carlo methods over other techniques increases as the dimensions (sources of uncertainty) of the problem increase.
Monte Carlo methods were first introduced to finance in 1964 by David B. Hertz
David B. Hertz
David Bendel Hertz is known for his contributions to operations research in general, and specifically for pioneering the use of Monte Carlo methods in finance. He was a director at McKinsey & Company and at Arthur Andersen ....
through his Harvard Business Review
Harvard Business Review
Harvard Business Review is a general management magazine published since 1922 by Harvard Business School Publishing, owned by the Harvard Business School. A monthly research-based magazine written for business practitioners, it claims a high ranking business readership among academics, executives,...
article, discussing their application in Corporate Finance
Corporate finance
Corporate finance is the area of finance dealing with monetary decisions that business enterprises make and the tools and analysis used to make these decisions. The primary goal of corporate finance is to maximize shareholder value while managing the firm's financial risks...
. In 1977, Phelim Boyle
Phelim Boyle
Phelim Boyle , a distinguished professor and actuary, is a professor of finance in the Laurier School of Business & Economics at Wilfrid Laurier University in Canada and is a pioneer of quantitative finance. He is best known for initiating the use of Monte Carlo methods in option pricing...
pioneered the use of simulation in derivative valuation
Derivative (finance)
A derivative instrument is a contract between two parties that specifies conditions—in particular, dates and the resulting values of the underlying variables—under which payments, or payoffs, are to be made between the parties.Under U.S...
in his seminal Journal of Financial Economics
Journal of Financial Economics
The Journal of Financial Economics or JFE, is a peer-reviewed academic journal covering the theory of financial economics. Together with the Journal of Finance and the Review of Financial Studies, it is considered to be among the top three finance journal. The editor is Bill Schwert...
paper.
This article discusses typical financial problems in which Monte Carlo methods are used. It also touches on the use of so-called "quasi-random" methods such as the use of Sobol sequence
Sobol sequence
Sobol sequences are an example of quasi-random low-discrepancy sequences. They were first introduced by I.M.Sobol'In Cyrillic as "Илья Меерович Соболь", as per...
s.
Overview
The Monte Carlo Method encompasses any technique of statistical sampling employed to approximate solutions to quantitative problems. Essentially, the Monte Carlo method solves a problem by directly simulating the underlying (physical) process and then calculating the (average) result of the process. This very general approach is valid in areas such as physicsPhysics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, chemistry
Chemistry
Chemistry is the science of matter, especially its chemical reactions, but also its composition, structure and properties. Chemistry is concerned with atoms and their interactions with other atoms, and particularly with the properties of chemical bonds....
, computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
etc.
In finance
Finance
"Finance" is often defined simply as the management of money or “funds” management Modern finance, however, is a family of business activity that includes the origination, marketing, and management of cash and money surrogates through a variety of capital accounts, instruments, and markets created...
, the Monte Carlo method is used to simulate the various sources of uncertainty that affect the value of the instrument, portfolio
Portfolio (finance)
Portfolio is a financial term denoting a collection of investments held by an investment company, hedge fund, financial institution or individual.-Definition:The term portfolio refers to any collection of financial assets such as stocks, bonds and cash...
or investment
Investment
Investment has different meanings in finance and economics. Finance investment is putting money into something with the expectation of gain, that upon thorough analysis, has a high degree of security for the principal amount, as well as security of return, within an expected period of time...
in question, and to then calculate a representative value given these possible values of the underlying inputs. In terms of financial theory
Financial economics
Financial Economics is the branch of economics concerned with "the allocation and deployment of economic resources, both spatially and across time, in an uncertain environment"....
, this, essentially, is an application of risk neutral valuation; see also risk neutrality.
Some examples:
- In Corporate FinanceCorporate financeCorporate finance is the area of finance dealing with monetary decisions that business enterprises make and the tools and analysis used to make these decisions. The primary goal of corporate finance is to maximize shareholder value while managing the firm's financial risks...
, project financeProject financeProject finance is the long term financing of infrastructure and industrial projects based upon the projected cash flows of the project rather than the balance sheets of the project sponsors...
and real options analysisReal options analysisReal options valuation, also often termed Real options analysis, applies option valuation techniques to capital budgeting decisions. A real option itself, is the right — but not the obligation — to undertake some business decision; typically the option to make, abandon, expand, or contract a...
, Monte Carlo Methods are used by financial analystFinancial analystA financial analyst, securities analyst, research analyst, equity analyst, or investment analyst is a person who performs financial analysis for external or internal clients as a core part of the job.-Job:...
s who wish to construct "stochasticStochasticStochastic refers to systems whose behaviour is intrinsically non-deterministic. A stochastic process is one whose behavior is non-deterministic, in that a system's subsequent state is determined both by the process's predictable actions and by a random element. However, according to M. Kac and E...
" or probabilistic financial models as opposed to the traditional static and deterministicDeterministic system (mathematics)In mathematics, a deterministic system is a system in which no randomness is involved in the development of future states of the system. A deterministic model will thus always produce the same output from a given starting condition or initial state.-Examples:...
models. Here, in order to analyze the characteristics of a project’s net present valueNet present valueIn finance, the net present value or net present worth of a time series of cash flows, both incoming and outgoing, is defined as the sum of the present values of the individual cash flows of the same entity...
(NPV), the cash flow components that are (heavily ) impacted by uncertaintyUncertaintyUncertainty is a term used in subtly different ways in a number of fields, including physics, philosophy, statistics, economics, finance, insurance, psychology, sociology, engineering, and information science...
are modeled, incorporating any correlationCorrelationIn statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
, mathematically reflecting their "random characteristics". Then, these results are combined in a histogramHistogramIn statistics, a histogram is a graphical representation showing a visual impression of the distribution of data. It is an estimate of the probability distribution of a continuous variable and was first introduced by Karl Pearson...
of NPV (i.e. the project’s probability distributionProbability distributionIn probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
), and the average NPV of the potential investment - as well as its volatilityVolatility (finance)In finance, volatility is a measure for variation of price of a financial instrument over time. Historic volatility is derived from time series of past market prices...
and other sensitivities - is observed. This distribution allows, for example, for an estimate of the probability that the project has a net present value greater than zero (or any other value). See further under Corporate finance.
- In valuing an option on equityOption (finance)In finance, an option is a derivative financial instrument that specifies a contract between two parties for a future transaction on an asset at a reference price. The buyer of the option gains the right, but not the obligation, to engage in that transaction, while the seller incurs the...
, the simulation generates several thousand possible (but random) price paths for the underlying share, with the associated exerciseExercise (options)The owner of an option contract may exercise it, indicating that the financial transaction specified by the contract is to be enacted immediately between the two parties, and the contract itself is terminated...
value (i.e. "payoff") of the option for each path. These payoffs are then averaged and discountedPresent valuePresent value, also known as present discounted value, is the value on a given date of a future payment or series of future payments, discounted to reflect the time value of money and other factors such as investment risk...
to today, and this result is the value of the option today; see Monte Carlo methods for option pricing for discussion as to further - and more complexExotic optionIn finance, an exotic option is a derivative which has features making it more complex than commonly traded products . These products are usually traded over-the-counter , or are embedded in structured notes....
- option modelling.
- To value bondsBond (finance)In finance, a bond is a debt security, in which the authorized issuer owes the holders a debt and, depending on the terms of the bond, is obliged to pay interest to use and/or to repay the principal at a later date, termed maturity...
, and bond optionBond optionIn finance, a bond option is an option to buy or sell a bond at a certain price on or before the option expiry date. These instruments are typically traded OTC....
s, the underlying source of uncertainty which is simulated is the short rate - the annualized interest rateInterest rateAn interest rate is the rate at which interest is paid by a borrower for the use of money that they borrow from a lender. For example, a small company borrows capital from a bank to buy new assets for their business, and in return the lender receives interest at a predetermined interest rate for...
at which an entity can borrow money for a given period of time; see Short-rate model. For each possible evolution of interest rateInterest rateAn interest rate is the rate at which interest is paid by a borrower for the use of money that they borrow from a lender. For example, a small company borrows capital from a bank to buy new assets for their business, and in return the lender receives interest at a predetermined interest rate for...
s we observe a different yield curveYield curveIn finance, the yield curve is the relation between the interest rate and the time to maturity, known as the "term", of the debt for a given borrower in a given currency. For example, the U.S. dollar interest rates paid on U.S...
and a different resultant bond price. To determine the bond value, these bond prices are then averaged; to value the bond option, as for equity options, the corresponding exercise valueExercise (options)The owner of an option contract may exercise it, indicating that the financial transaction specified by the contract is to be enacted immediately between the two parties, and the contract itself is terminated...
s are averaged and present valued. A similar approach is used in valuing swapsSwap (finance)In finance, a swap is a derivative in which counterparties exchange certain benefits of one party's financial instrument for those of the other party's financial instrument. The benefits in question depend on the type of financial instruments involved...
and swaptionSwaptionA swaption is an option granting its owner the right but not the obligation to enter into an underlying swap. Although options can be traded on a variety of swaps, the term "swaption" typically refers to options on interest rate swaps....
s.
- Monte Carlo Methods are used for portfolioPortfolio (finance)Portfolio is a financial term denoting a collection of investments held by an investment company, hedge fund, financial institution or individual.-Definition:The term portfolio refers to any collection of financial assets such as stocks, bonds and cash...
evaluation. Here, for each sample, the correlatedCorrelationIn statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
behaviour of the factors impacting the component instruments is simulated over time, the resultant value of each instrument is calculated, and the portfolio value is then observed. As for corporate finance, above, the various portfolio values are then combined in a histogramHistogramIn statistics, a histogram is a graphical representation showing a visual impression of the distribution of data. It is an estimate of the probability distribution of a continuous variable and was first introduced by Karl Pearson...
, and the statistical characteristicsDescriptive statisticsDescriptive statistics quantitatively describe the main features of a collection of data. Descriptive statistics are distinguished from inferential statistics , in that descriptive statistics aim to summarize a data set, rather than use the data to learn about the population that the data are...
of the portfolio are observed, and the portfolio assessed as required. A similar approach is used in calculating value at risk.
- Monte Carlo Methods are used for personal financial planning. For instance, by simulating the overall market, the chances of a 401(k)401(k)A 401 is a type of retirement savings account in the United States, which takes its name from subsection of the Internal Revenue Code . A contributor can begin to withdraw funds after reaching the age of 59 1/2 years...
allowing for retirementRetirementRetirement is the point where a person stops employment completely. A person may also semi-retire by reducing work hours.Many people choose to retire when they are eligible for private or public pension benefits, although some are forced to retire when physical conditions don't allow the person to...
on a target income can be calculated. As appropriate, the worker in question can then take greater risks with the retirement portfolio or start saving more money.
Although Monte Carlo methods provide flexibility, and can handle multiple sources of uncertainty, the use of these techniques is nevertheless not always appropriate. In general, simulation methods are preferred to other valuation techniques only when there are several state variables (i.e. several sources of uncertainty). These techniques are also of limited use in valuing American style derivatives. See below.
Level of complexity
Many problems in mathematical financeMathematical finance
Mathematical finance is a field of applied mathematics, concerned with financial markets. The subject has a close relationship with the discipline of financial economics, which is concerned with much of the underlying theory. Generally, mathematical finance will derive and extend the mathematical...
entail the computation of a particular integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
(for instance the problem of finding the arbitrage-free value of a particular derivative
Derivative (finance)
A derivative instrument is a contract between two parties that specifies conditions—in particular, dates and the resulting values of the underlying variables—under which payments, or payoffs, are to be made between the parties.Under U.S...
). In many cases these integrals can be valued analytically, and in still more cases they can be valued using numerical integration
Numerical integration
In numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of...
, or computed using a partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
(PDE). However when the number of dimensions (or degrees of freedom) in the problem is large, PDEs and numerical integrals become intractable, and in these cases Monte Carlo method
Monte Carlo method
Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
s often give better results.
For more than three or four state variables, formulae such as Black Scholes (i.e. analytic solutions) do not exist, while other numerical methods such as the Binomial options pricing model
Binomial options pricing model
In finance, the binomial options pricing model provides a generalizable numerical method for the valuation of options. The binomial model was first proposed by Cox, Ross and Rubinstein in 1979. Essentially, the model uses a “discrete-time” model of the varying price over time of the underlying...
and finite difference method
Finite difference method
In mathematics, finite-difference methods are numerical methods for approximating the solutions to differential equations using finite difference equations to approximate derivatives.- Derivation from Taylor's polynomial :...
s face several difficulties and are not practical. In these cases, Monte Carlo methods converge to the solution more quickly than numerical methods, require less memory and are easier to program. For simpler situations, however, simulation is not the better solution because it is very time-consuming and computationally intensive.
Monte Carlo methods can deal with derivatives which have path dependent payoffs in a fairly straight forward manner. On the other hand Finite Difference (PDE) solvers struggle with path dependence.
American options
Monte-Carlo methods are harder to use with American optionOption style
In finance, the style or family of an option is a general term denoting the class into which the option falls, usually defined by the dates on which the option may be exercised. The vast majority of options are either European or American options. These options - as well as others where the...
s. This is because, in contrast to a partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
, the Monte Carlo method really only estimates the option value assuming a given starting point and time.
However, for early exercise, we would also need to know the option value at the intermediate times between the simulation start time and the option expiry time. In the Black–Scholes PDE approach these prices are easily obtained, because the simulation runs backwards from the expiry date. In Monte-Carlo this information is harder to obtain, but it can be done for example using the least squares
Least squares
The method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
algorithm of Carriere (see link to original paper) which was made popular a few years later by Longstaff and Schwartz (see link to original paper).
Stochastic Grid Method (SGM) proposed by Jain and Oosterlee provides a general framework for pricing high dimensional American options (see link to original paper).
Mathematically
The fundamental theorem of arbitrage-free pricingFundamental theorem of arbitrage-free pricing
The fundamental theorems of arbitrage/finance provide necessary and sufficient conditions for a market to be arbitrage free and for a market to be complete. An arbitrage opportunity is a way of making money with no initial investment without any possibility of loss...
states that the value of a derivative is equal to the discounted expected value of the derivative payoff where the expectation
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
is taken under the risk-neutral measure
Risk-neutral measure
In mathematical finance, a risk-neutral measure, is a prototypical case of an equivalent martingale measure. It is heavily used in the pricing of financial derivatives due to the fundamental theorem of asset pricing, which implies that in a complete market a derivative's price is the discounted...
[1]. An expectation is, in the language of pure mathematics
Pure mathematics
Broadly speaking, pure mathematics is mathematics which studies entirely abstract concepts. From the eighteenth century onwards, this was a recognized category of mathematical activity, sometimes characterized as speculative mathematics, and at variance with the trend towards meeting the needs of...
, simply an integral with respect to the measure. Monte Carlo methods are ideally suited to evaluating difficult integrals (see also Monte Carlo method
Monte Carlo method
Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
).
Thus if we suppose that our risk-neutral probability space is
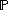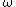and that we have a derivative H that depends on a set of underlying instruments . Then given a sample from the probability space the value of the derivative is 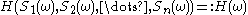. Today's value of the derivative is found by taking the expectation over all possible samples and discounting at the risk-free rate. I.e. the derivative has value: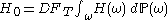where
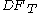is the discount factor corresponding to the risk-free rate to the final maturity date T years into the future.Now suppose the integral is hard to compute. We can approximate the integral by generating sample paths and then taking an average. Suppose we generate N samples then
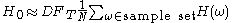
which is much easier to compute.
Sample paths for standard models
In finance, underlying random variables (such as an underlying stock price) are usually assumed to follow a path that is a function of a Brownian motionBrownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
2. For example in the standard Black–Scholes model, the stock price evolves as
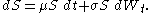
To sample a path following this distribution from time 0 to T, we chop the time interval into M units of length
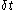, and approximate the Brownian motion over the interval 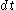by a single normal variable of mean 0 and variance 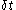. This leads to a sample path of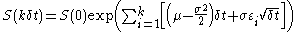for each k between 1 and M. Here each
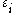is a draw from a standard normal distribution.Let us suppose that a derivative H pays the average value of S between 0 and T then a sample path
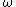corresponds to a set and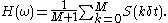We obtain the Monte-Carlo value of this derivative by generating N lots of M normal variables, creating N sample paths and so N values of H, and then taking the average.
Commonly the derivative will depend on two or more (possibly correlated) underlyings. The method here can be extended to generate sample paths of several variables, where the normal variables building up the sample paths are appropriately correlated.
It follows from the central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
that quadrupling the number of sample paths approximately halves the error in the simulated price (i.e. the error has order
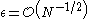convergence in the sense of standard deviation of the solution).In practice Monte Carlo methods are used for European-style derivatives involving at least three variables (more direct methods involving numerical integration can usually be used for those problems with only one or two underlyings. See Monte Carlo option model
Monte Carlo option model
In mathematical finance, a Monte Carlo option model uses Monte Carlo methods to calculate the value of an option with multiple sources of uncertainty or with complicated features....
.
Greeks
Estimates for the "Greeks" of an option i.e. the (mathematical) derivatives of option value with respect to input parameters, can be obtained by numerical differentiation. This can be a time-consuming process (an entire Monte Carlo run must be performed for each "bump" or small change in input parameters). Further, taking numerical derivatives tends to emphasize the error (or noise) in the Monte Carlo value - making it necessary to simulate with a large number of sample paths. Practitioners regard these points as a key problem with using Monte Carlo methods.Variance reduction
Square root convergence is slow, and so using the naive approach described above requires using a very large number of sample paths (1 million, say, for a typical problem) in order to obtain an accurate result. Remember that an estimator for the price of a derivative is a random variable, and in the framework of a risk-management activity, uncertainty on the price of a portfolio of derivatives and/or on its risks can lead to suboptimal risk-management decisions.This state of affairs can be mitigated by variance reduction
Variance reduction
In mathematics, more specifically in the theory of Monte Carlo methods, variance reduction is a procedure used to increase the precision of the estimates that can be obtained for a given number of iterations. Every output random variable from the simulation is associated with a variance which...
techniques.
Antithetic paths
A simple technique is, for every sample path obtained, to take its antithetic path — that is given a path to also take . Not only does this reduce the number of normal samples to be taken to generate N paths, but also, under same conditions, reduces the variance of the sample paths, improving the accuracy.Control variate method
It is also natural to use a control variateControl variate
The control variates method is a variance reduction technique used in Monte Carlo methods. It exploits information about the errors in estimates of known quantities to reduce the error of an estimate of an unknown quantity.-Underlying principle:...
. Let us suppose that we wish to obtain the Monte Carlo value of a derivative H, but know the value analytically of a similar derivative I. Then H* = (Value of H according to Monte Carlo) + B*[(Value of I analytically) − (Value of I according to same Monte Carlo paths)] is a better estimate, where B is covar(H,I)/var(H).
The intuition behind that technique, when applied to derivatives, is the following: note that the source of the variance of a derivative will be directly dependent on the risks (e.g. delta, vega) of this derivative. This is because any error on, say, the estimator for the forward value of an underlier, will generate a corresponding error depending on the delta of the derivative with respect to this forward value. The simplest example to demonstrate this consists in comparing the error when pricing an at-the-money call and an at-the-money straddle (i.e. call+put), which has a much lower delta.
Therefore, a standard way of choosing the derivative I consists in choosing a replicating portfolio
Replicating portfolio
In the valuation of a life insurance company, the actuary considers a series of future uncertain cashflows and attempts to put a value on these cashflows...
s of options for H. In practice, one will price H without variance reduction, calculate deltas and vegas, and then use a combination of calls and puts that have the same deltas and vegas as control variate.
Importance sampling
Importance sampling consists of simulating the Monte Carlo paths using a different probability distribution (also known as a change of measure) that will give more likelihood for the simulated underlier to be located in the area where the derivative's payoff has the most convexity (for example, close to the strike in the case of a simple option). The simulated payoffs are then not simply averaged as in the case of a simple Monte Carlo, but are first multiplied by the likelihood ratio between the modified probability distribution and the original one (which is obtained by analytical formulas specific for the probability distribution). This will ensure that paths whose probability have been arbitrarily enhanced by the change of probability distribution are weighted with a low weight (this is how the variance gets reduced).This technique can be particularly useful when calculating risks on a derivative. When calculating the delta using a Monte Carlo method, the most straightforward way is the black-box technique consisting in doing a Monte Carlo on the original market data and another one on the changed market data, and calculate the risk by doing the difference. Instead, the importance sampling method consists in doing a Monte Carlo in an arbitrary reference market data (ideally one in which the variance is as low as possible), and calculate the prices using the weight-changing technique described above. This results in a risk that will be much more stable than the one obtained through the black-box approach.
Quasi-random (low-discrepancy) methods
Instead of generating sample paths randomly, it is possible to systematically (and in fact completely deterministically, despite the "quasi-random" in the name) select points in a probability spaces so as to optimally "fill up" the space. The selection of points is a low-discrepancy sequenceLow-discrepancy sequence
In mathematics, a low-discrepancy sequence is a sequence with the property that for all values of N, its subsequence x1, ..., xN has a low discrepancy....
such as a Sobol sequence
Sobol sequence
Sobol sequences are an example of quasi-random low-discrepancy sequences. They were first introduced by I.M.Sobol'In Cyrillic as "Илья Меерович Соболь", as per...
. Taking averages of derivative payoffs at points in a low-discrepancy sequence is often more efficient than taking averages of payoffs at random points.
See also
- Quasi-Monte Carlo methods in finance
- Monte Carlo methodMonte Carlo methodMonte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
- Stock market simulatorStock market simulatorA stock market simulator is a program or application that attempts to reproduce or duplicate some or all features of a live stock market on a computer so that a player may practice trading stocks without financial risk.- Types :...
Articles
- Boyle, P., Broadie, M. and Glasserman, P. Monte Carlo Methods for Security Pricing. Journal of Economic Dynamics and Control, Volume 21, Issues 8-9, Pages 1267-1321
- Rubinstein, Samorodnitsky, Shaked. Antithetic Variates, Multivariate Dependence and Simulation of Stochastic Systems. Managemen Science, Vol. 31, No. 1, Jan 1985, pages 66–67
Software
- FairmatFairmatFairmat is a free-of-charge multi-platform software that allows to model financial contracts or projects with many contingencies by decomposing it into basic parts. Complex structures and dependencies are modeled using a graphical interface...
(freewareFreewareFreeware is computer software that is available for use at no cost or for an optional fee, but usually with one or more restricted usage rights. Freeware is in contrast to commercial software, which is typically sold for profit, but might be distributed for a business or commercial purpose in the...
) modeling and pricing complex options - MG Soft, (freewareFreewareFreeware is computer software that is available for use at no cost or for an optional fee, but usually with one or more restricted usage rights. Freeware is in contrast to commercial software, which is typically sold for profit, but might be distributed for a business or commercial purpose in the...
) valuation and Greeks of vanilla and exotic options - SimulAr Free Monte Carlo simulation ExcelMicrosoft ExcelMicrosoft Excel is a proprietary commercial spreadsheet application written and distributed by Microsoft for Microsoft Windows and Mac OS X. It features calculation, graphing tools, pivot tables, and a macro programming language called Visual Basic for Applications...
Add-in
External links
General- MonteCarlo Simulation in Finance, global-derivatives.com
- Monte Carlo Method, riskglossary.com
- The Monte Carlo Framework, Examples from Finance, Martin Haugh, Columbia UniversityColumbia UniversityColumbia University in the City of New York is a private, Ivy League university in Manhattan, New York City. Columbia is the oldest institution of higher learning in the state of New York, the fifth oldest in the United States, and one of the country's nine Colonial Colleges founded before the...
- Monte Carlo techniques applied to finance, Simon Leger
Derivative valuation
- Monte Carlo Simulation, Prof. Don M. Chance, Louisiana State UniversityLouisiana State UniversityLouisiana State University and Agricultural and Mechanical College, most often referred to as Louisiana State University, or LSU, is a public coeducational university located in Baton Rouge, Louisiana. The University was founded in 1853 in what is now known as Pineville, Louisiana, under the name...
- Option pricing by simulation, Bernt Arne Ødegaard, Norwegian School of ManagementNorwegian School of ManagementBI Norwegian Business School former name BI Norwegian School of Management is the largest business school in Norway and the second largest in all of Europe. BI has in total 6 campuses with the main one located in Oslo.-History:...
- Applications of Monte Carlo Methods in Finance: Option Pricing, Y. Lai and J. Spanier, Claremont Graduate UniversityClaremont Graduate UniversityClaremont Graduate University is a private, all-graduate research university located in Claremont, California, a city east of downtown Los Angeles...
- Monte Carlo Derivative valuation, contd., Timothy L. Krehbiel, Oklahoma State University–StillwaterOklahoma State University–StillwaterOklahoma State University–Stillwater is a land-grant, sun-grant, coeducational public research university located in Stillwater, Oklahoma, USA. OSU was founded in 1890 under the Morrill Act...
- Pricing complex options using a simple Monte Carlo Simulation, Peter Fink - reprint at quantnotes.com
- Least-Squares Monte-Carlo for American options by Carriere, 1996, ideas.repec.org
- Least-Squares Monte-Carlo for American options by Longstaff and Schwartz, 2001, repositories.cdlib.org
- Using simulation for option pricing, John Charnes
- Stochastic Grid Method for Pricing High-Dimensional American Options, S. Jain and C.W. Oosterlee
Corporate Finance
- Real Options with Monte Carlo Simulation, Marco Dias, Pontifícia Universidade Católica do Rio de JaneiroPontifícia Universidade Católica do Rio de JaneiroThe Pontifícia Universidade Católica do Rio de Janeiro is a private and non-profit Catholic university, located in Rio de Janeiro, the second largest city of Brazil...
- Using simulation to calculate the NPV of a project, investmentscience.com
- Simulations, Decision Trees and Scenario Analysis in Valuation Prof. Aswath DamodaranAswath DamodaranAswath Damodaran is a Professor of Finance at the Stern School of Business at New York University , where he teaches corporate finance and equity valuation...
, Stern School of Business - The Monte Carlo method in Excel Prof. André Farber Solvay Business School
- Sales Forecasting, vertex42.com
- Pricing using Monte Carlo simulation, a practical example, Prof. Giancarlo Vercellino
Value at Risk and portfolio analysis
- Monte Carlo Value-at-Risk, riskglossary.com
Personal finance
- A Better Way to Size Up Your Nest Egg, Businessweek Online: January 22, 2001
- Online Monte Carlo retirement planner with source code, Jim Richmond, 2006
- Free spreadsheet-based retirement calculator and Monte Carlo simulator, by Eric C., 2008
- Financial Planning Using Random Walks, John Norstad, 2005
- Retirement Calculator by VestingPoint.com