
Low-discrepancy sequence
Encyclopedia
In mathematics
, a low-discrepancy sequence is a sequence
with the property that for all values of N, its subsequence x1, ..., xN has a low discrepancy.
Roughly speaking, the discrepancy of a sequence is low if the number of points in the sequence falling into an arbitrary set B is close to proportional to the measure
of B, as would happen on average (but not for particular samples) in the case of a uniform distribution
. Specific definitions of discrepancy differ regarding the choice of B (hyperspheres, hypercubes, etc.) and how the discrepancy for every B is computed (usually normalized) and combined (usually by taking the worst value).
Low-discrepancy sequences are also called quasi-random or sub-random sequences, due to their common use as a replacement of uniformly distributed random numbers
.
The "quasi" modifier is used to denote more clearly that the values of a low-discrepancy sequence are neither random nor pseudorandom, but such sequences share some properties of random variables and in certain applications such as the quasi-Monte Carlo method
their lower discrepancy is an important advantage.
At least three methods of numerical integration
can be phrased as follows.
Given a set {x1, ..., xN} in the interval[0,1] , approximate the integral of a function f as the average of the function evaluated at those points:

If the points are chosen as xi = i/N, this is the rectangle rule.
If the points are chosen to be randomly (or pseudorandomly) distributed, this is the Monte Carlo method
.
If the points are chosen as elements of a low-discrepancy sequence, this is the quasi-Monte Carlo method.
A remarkable result, the Koksma–Hlawka inequality (stated below), shows that the error of such a method can be bounded by the product of two terms, one of which depends only on f, and the other one is the discrepancy of the set {x1, ..., xN}.
It is convenient to construct the set {x1, ..., xN} in such a way that if a set with N+1 elements is constructed, the previous N elements need not be recomputed.
The rectangle rule uses points set which have low discrepancy, but in general the elements must be recomputed if N is increased.
Elements need not be recomputed in the Monte Carlo method if N is increased,
but the point sets do not have minimal discrepancy.
By using low-discrepancy sequences, the quasi-Monte Carlo method has the desirable features of the other two methods.

where
λs is the s-dimensional Lebesgue measure
,
A(B;P) is the number of points in P that fall into B,
and J is the set of s-dimensional intervals or boxes of the form

where .
.
The star-discrepancy D*N(P) is defined similarly, except that the supremum is taken over the set J* of intervals of the form

where ui is in the half-open interval[0, 1) .
The two are related by

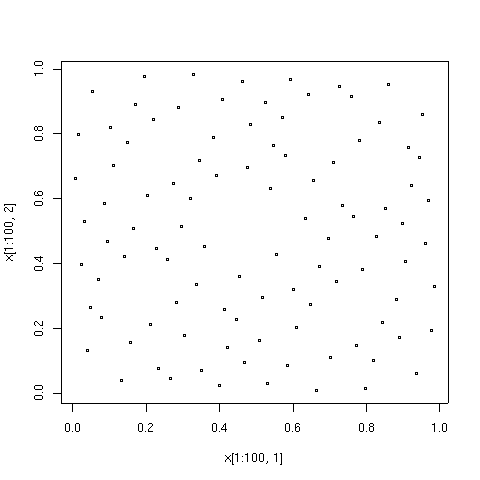
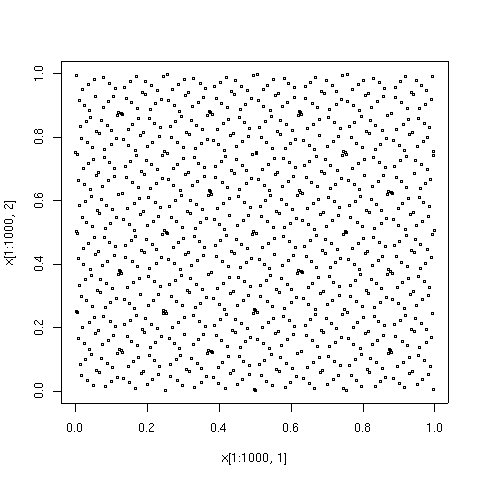
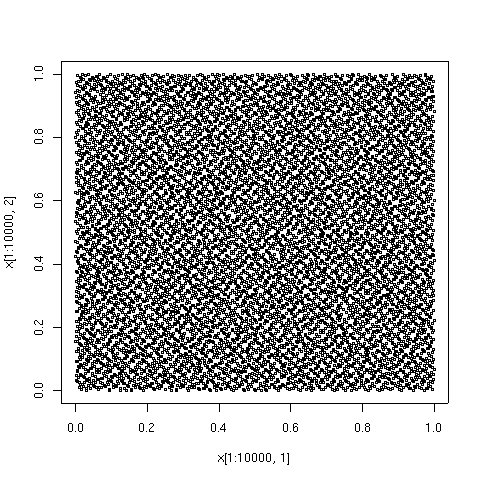
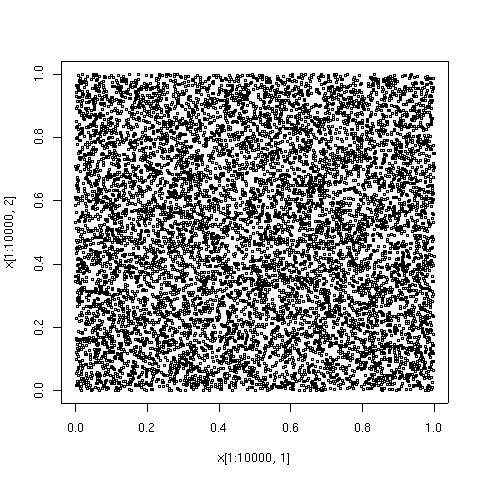
For comparison, 10000 elements of a sequence of pseudorandom points are also shown.
The low-discrepancy sequence was generated by TOMS
algorithm 659.
An implementation of the algorithm in Fortran
is available from Netlib
.
Īs = [0, 1] × ... × [0, 1].
Let f have bounded variation
V(f) on Īs in the sense of Hardy and Krause.
Then for any x1, ..., xN
in Is =
[ 0, 1) × ... ×
[ 0, 1) ,
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a low-discrepancy sequence is a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
with the property that for all values of N, its subsequence x1, ..., xN has a low discrepancy.
Roughly speaking, the discrepancy of a sequence is low if the number of points in the sequence falling into an arbitrary set B is close to proportional to the measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
of B, as would happen on average (but not for particular samples) in the case of a uniform distribution
Uniform distribution
-Probability theory:* Discrete uniform distribution* Continuous uniform distribution-Other:* "Uniform distribution modulo 1", see Equidistributed sequence*Uniform distribution , a type of species distribution* Distribution of military uniforms...
. Specific definitions of discrepancy differ regarding the choice of B (hyperspheres, hypercubes, etc.) and how the discrepancy for every B is computed (usually normalized) and combined (usually by taking the worst value).
Low-discrepancy sequences are also called quasi-random or sub-random sequences, due to their common use as a replacement of uniformly distributed random numbers
Random sequence
The concept of a random sequence is essential in probability theory and statistics. The concept generally relies on the notion of a sequence of random variables and many statistical discussions begin with the words "let X1,...,Xn be independent random variables...". Yet as D. H. Lehmer stated in...
.
The "quasi" modifier is used to denote more clearly that the values of a low-discrepancy sequence are neither random nor pseudorandom, but such sequences share some properties of random variables and in certain applications such as the quasi-Monte Carlo method
Quasi-Monte Carlo method
In numerical analysis, a quasi-Monte Carlo method is a method for the computation of an integral that is based on low-discrepancy sequences...
their lower discrepancy is an important advantage.
At least three methods of numerical integration
Numerical integration
In numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of...
can be phrased as follows.
Given a set {x1, ..., xN} in the interval

If the points are chosen as xi = i/N, this is the rectangle rule.
If the points are chosen to be randomly (or pseudorandomly) distributed, this is the Monte Carlo method
Monte Carlo method
Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
.
If the points are chosen as elements of a low-discrepancy sequence, this is the quasi-Monte Carlo method.
A remarkable result, the Koksma–Hlawka inequality (stated below), shows that the error of such a method can be bounded by the product of two terms, one of which depends only on f, and the other one is the discrepancy of the set {x1, ..., xN}.
It is convenient to construct the set {x1, ..., xN} in such a way that if a set with N+1 elements is constructed, the previous N elements need not be recomputed.
The rectangle rule uses points set which have low discrepancy, but in general the elements must be recomputed if N is increased.
Elements need not be recomputed in the Monte Carlo method if N is increased,
but the point sets do not have minimal discrepancy.
By using low-discrepancy sequences, the quasi-Monte Carlo method has the desirable features of the other two methods.
Definition of discrepancy
The discrepancy of a set P = {x1, ..., xN} is defined, using Niederreiter's notation, as
where
λs is the s-dimensional Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
,
A(B;P) is the number of points in P that fall into B,
and J is the set of s-dimensional intervals or boxes of the form

where
 .
.The star-discrepancy D*N(P) is defined similarly, except that the supremum is taken over the set J* of intervals of the form

where ui is in the half-open interval
The two are related by

Graphical examples
The points plotted below are the first 100, 1000, and 10000 elements in a sequence of the Sobol' type.For comparison, 10000 elements of a sequence of pseudorandom points are also shown.
The low-discrepancy sequence was generated by TOMS
Toms
V. T. Thomas a.k.a. Toms is a cartoonist from Kerala, India. He is the creator of the cartoon characters Boban and Molly ....
algorithm 659.
An implementation of the algorithm in Fortran
Fortran
Fortran is a general-purpose, procedural, imperative programming language that is especially suited to numeric computation and scientific computing...
is available from Netlib
Netlib
Netlib is a repository of software for scientific computing maintained by AT&T, Bell Laboratories, the University of Tennessee and Oak Ridge National Laboratory. Netlib comprises a large number of separate programs and libraries...
.




The Koksma–Hlawka inequality
Let Īs be the s-dimensional unit cube,Īs = [0, 1] × ... × [0, 1].
Let f have bounded variation
Bounded variation
In mathematical analysis, a function of bounded variation, also known as a BV function, is a real-valued function whose total variation is bounded : the graph of a function having this property is well behaved in a precise sense...
V(f) on Īs in the sense of Hardy and Krause.
Then for any x1, ..., xN
in Is =
-

The KoksmaJurjen Ferdinand KoksmaJurjen Ferdinand Koksma was a Dutch mathematician who specialized in analytic number theory....
-Hlawka inequality is sharp in the following sense: For any point set {x1,...,xN} in Is and any , there is a function f with bounded variation and V(f)=1 such that
, there is a function f with bounded variation and V(f)=1 such that

Therefore, the quality of a numerical integration rule depends only on the discrepancy D*N(x1,...,xN).
The formula of Hlawka-Zaremba
Let . For
. For  we
we
write
and denote by the point obtained from x by replacing the
the point obtained from x by replacing the
coordinates not in u by .
.
Then
The
Applying the Cauchy-Schwarz inequality version of the Koksma–Hlawka inequality
version of the Koksma–Hlawka inequality
for integrals and sums
to the Hlawka-Zaremba identity, we obtain
an version of the Koksma–Hlawka inequality:
version of the Koksma–Hlawka inequality:
where
and
The Erdős–Turan–Koksma inequality
It is computationally hard to find the exact value of the discrepancy of large point sets. The Erdős–TuránTuranTūrān is the Persian name for Central Asia, literally meaning "the land of the Tur". As described below, the original Turanians are an Iranian tribe of the Avestan age. As a people the "Turanian" are one of the two Iranian peoples both descending from the Persian Fereydun but with different...
–KoksmaJurjen Ferdinand KoksmaJurjen Ferdinand Koksma was a Dutch mathematician who specialized in analytic number theory....
inequality provides an upper bound.
Let x1,...,xN be points in Is and H be an arbitrary positive integer. Then

where

The main conjectures
Conjecture 1. There is a constant cs depending only on the dimension s, such that

for any finite point set {x1,...,xN}.
Conjecture 2. There is a constant c's depending only on s, such that

for any infinite sequence x1,x2,x3,....
These conjectures are equivalent. They have been proved for s ≤ 2 by W. M. Schmidt. In higher dimensions, the corresponding problem is still open. The best-known lower bounds are due to K. F. Roth.
The best-known sequences
Constructions of sequences are known such that

where C is a certain constant, depending on the sequence. After Conjecture 2, these sequences are believed to have the best possible order of convergence. See also: van der Corput sequenceVan der Corput sequenceA van der Corput sequence is a low-discrepancy sequence over the unit interval first published in 1935 by the Dutch mathematician J. G. van der Corput. It is constructed by reversing the base n representation of the sequence of natural numbers...
, Halton sequencesHalton sequencesIn statistics, Halton sequences are sequences used to generate points in space for numerical methods such as Monte Carlo simulations. Although these sequences are deterministic they are of low discrepancy, that is, appear to be random for many purposes. They were first introduced in 1960 and are...
, Sobol sequenceSobol sequenceSobol sequences are an example of quasi-random low-discrepancy sequences. They were first introduced by I.M.Sobol'In Cyrillic as "Илья Меерович Соболь", as per...
s.
Lower bounds
Let s = 1. Then

for any finite point set {x1, ..., xN}.
Let s = 2. W. M. Schmidt proved that for any finite point set {x1, ..., xN},

where

For arbitrary dimensions s > 1, K.F. Roth proved that

for any finite point set {x1, ..., xN}.
This bound is the best known for s > 3.
Applications
- IntegrationIntegralIntegration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
- OptimizationOptimization (mathematics)In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
- Statistical samplingSampling (statistics)In statistics and survey methodology, sampling is concerned with the selection of a subset of individuals from within a population to estimate characteristics of the whole population....
External links
- Collected Algorithms of the ACM (See algorithms 647, 659, and 738.)
- GNU Scientific Library Quasi-Random Sequences
- Integration

