Uncertainty
Encyclopedia
Uncertainty is a term used in subtly different ways in a number of fields, including physics
, philosophy
, statistics
, economics
, finance
, insurance
, psychology
, sociology
, engineering
, and information science
. It applies to predictions of future events, to physical measurements already made, or to the unknown.
economist Frank Knight
(1921) established the important distinction between risk
and uncertainty:
Although the terms are used in various ways among the general public, many specialists in decision theory
, statistics
and other quantitative fields have defined uncertainty, risk, and their measurement as:
There are other taxonomies of uncertainties and decisions that include a broader sense of uncertainty and how it should be approached from an ethics perspective:
For example, if you do not know whether it will rain tomorrow, then you have a state of uncertainty. If you apply probabilities to the possible outcomes using weather forecasts or even just a calibrated probability assessment
, you have quantified the uncertainty. Suppose you quantify your uncertainty as a 90% chance of sunshine. If you are planning a major, costly, outdoor event for tomorrow then you have risk since there is a 10% chance of rain and rain would be undesirable. Furthermore, if this is a business event and you would lose $100,000 if it rains, then you have quantified the risk (a 10% chance of losing $100,000). These situations can be made even more realistic by quantifying light rain vs. heavy rain, the cost of delays vs. outright cancellation, etc.
Some may represent the risk in this example as the "expected opportunity loss" (EOL) or the chance of the loss multiplied by the amount of the loss (10% × $100,000 = $10,000). That is useful if the organizer of the event is "risk neutral," which most people are not. Most would be willing to pay a premium to avoid the loss. An insurance
company, for example, would compute an EOL as a minimum for any insurance coverage, then add on to that other operating costs and profit. Since many people are willing to buy insurance for many reasons, then clearly the EOL alone is not the perceived value of avoiding the risk.
Quantitative uses of the terms uncertainty and risk are fairly consistent from fields such as probability theory
, actuarial science
, and information theory
. Some also create new terms without substantially changing the definitions of uncertainty or risk. For example, surprisal is a variation on uncertainty sometimes used in information theory
. But outside of the more mathematical uses of the term, usage may vary widely. In cognitive psychology
, uncertainty can be real, or just a matter of perception, such as expectation
s, threats, etc.
Vagueness or ambiguity are sometimes described as "second order uncertainty," where there is uncertainty even about the definitions of uncertain states or outcomes. The difference here is that this uncertainty is about the human definitions and concepts, not an objective fact of nature. It has been argued that ambiguity, however, is always avoidable while uncertainty (of the "first order" kind) is not necessarily avoidable.
Uncertainty may be purely a consequence of a lack of knowledge of obtainable facts. That is, you may be uncertain about whether a new rocket design will work, but this uncertainty can be removed with further analysis and experimentation. At the subatomic level, however, uncertainty may be a fundamental and unavoidable property of the universe. In quantum mechanics
, the Heisenberg Uncertainty Principle puts limits on how much an observer can ever know about the position and velocity of a particle. This may not just be ignorance of potentially obtainable facts but that there is no fact to be found. There is some controversy in physics as to whether such uncertainty is an irreducible property of nature or if there are "hidden variables" that would describe the state of a particle even more exactly than Heisenberg's uncertainty principle allows.
In metrology
, physics
, and engineering
, the uncertainty or margin of error
of a measurement is stated by giving a range of values likely to enclose the true value. This may be denoted by error bar
s on a graph, or by the following notations:
The middle notation is used when the error is not symmetrical about the value – for example
. This can occur when using a logarithmic scale, for example. The latter "concise notation" is used for example by IUPAC in stating the atomic mass of elements
. There, the uncertainty given in parenthesis applies to the least significant figure(s) of x prior to the parenthesized value (ie. counting from rightmost digit to left). For instance, stands for , while stands for .
Often, the uncertainty of a measurement is found by repeating the measurement enough times to get a good estimate of the standard deviation
of the values. Then, any single value has an uncertainty equal to the standard deviation. However, if the values are averaged, then the mean measurement value has a much smaller uncertainty, equal to the standard error
of the mean, which is the standard deviation divided by the square root of the number of measurements.
When the uncertainty represents the standard error of the measurement, then about 68.2% of the time, the true value of the measured quantity falls within the stated uncertainty range. For example, it is likely that for 31.8% of the atomic mass values given on the list of elements by atomic mass, the true value lies outside of the stated range. If the width of the interval is doubled, then probably only 4.6% of the true values lie outside the doubled interval, and if the width is tripled, probably only 0.3% lie outside. These values follow from the properties of the normal distribution, and they apply only if the measurement process produces normally distributed errors. In that case, the quoted standard error
s are easily converted to 68.3% ("one sigma"), 95.4% ("two sigma"), or 99.7% ("three sigma") confidence interval
s.
In this context, uncertainty depends on both the accuracy and precision
of the measurement instrument. The lower the accuracy and precision of an instrument, the larger the measurement uncertainty is. Notice that precision is often determined as the standard deviation
of the repeated measures of a given value, namely using the same method described above to assess measurement uncertainty. However, this method is correct only when the instrument is accurate. When it is inaccurate, the uncertainty is larger than the standard deviation
of the repeated measures, and it appears evident that the uncertainty does not depend only on instrumental precision.
Uncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
, philosophy
Philosophy
Philosophy is the study of general and fundamental problems, such as those connected with existence, knowledge, values, reason, mind, and language. Philosophy is distinguished from other ways of addressing such problems by its critical, generally systematic approach and its reliance on rational...
, statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, economics
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
, finance
Finance
"Finance" is often defined simply as the management of money or “funds” management Modern finance, however, is a family of business activity that includes the origination, marketing, and management of cash and money surrogates through a variety of capital accounts, instruments, and markets created...
, insurance
Insurance
In law and economics, insurance is a form of risk management primarily used to hedge against the risk of a contingent, uncertain loss. Insurance is defined as the equitable transfer of the risk of a loss, from one entity to another, in exchange for payment. An insurer is a company selling the...
, psychology
Psychology
Psychology is the study of the mind and behavior. Its immediate goal is to understand individuals and groups by both establishing general principles and researching specific cases. For many, the ultimate goal of psychology is to benefit society...
, sociology
Sociology
Sociology is the study of society. It is a social science—a term with which it is sometimes synonymous—which uses various methods of empirical investigation and critical analysis to develop a body of knowledge about human social activity...
, engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
, and information science
Information science
-Introduction:Information science is an interdisciplinary science primarily concerned with the analysis, collection, classification, manipulation, storage, retrieval and dissemination of information...
. It applies to predictions of future events, to physical measurements already made, or to the unknown.
Concepts
In his seminal work Risk, Uncertainty, and Profit University of ChicagoUniversity of Chicago
The University of Chicago is a private research university in Chicago, Illinois, USA. It was founded by the American Baptist Education Society with a donation from oil magnate and philanthropist John D. Rockefeller and incorporated in 1890...
economist Frank Knight
Frank Knight
Frank Hyneman Knight was an American economist who spent most of his career at the University of Chicago, where he became one of the founders of the Chicago school. Nobel laureates James M. Buchanan, Milton Friedman and George Stigler were all students of Knight at Chicago. Knight supervised...
(1921) established the important distinction between risk
Risk
Risk is the potential that a chosen action or activity will lead to a loss . The notion implies that a choice having an influence on the outcome exists . Potential losses themselves may also be called "risks"...
and uncertainty:
Although the terms are used in various ways among the general public, many specialists in decision theory
Decision theory
Decision theory in economics, psychology, philosophy, mathematics, and statistics is concerned with identifying the values, uncertainties and other issues relevant in a given decision, its rationality, and the resulting optimal decision...
, statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
and other quantitative fields have defined uncertainty, risk, and their measurement as:
- Uncertainty: The lack of certainty, A state of having limited knowledge where it is impossible to exactly describe existing state or future outcome, more than one possible outcome.
- Measurement of Uncertainty: A set of possible states or outcomes where probabilities are assigned to each possible state or outcome – this also includes the application of a probability density function to continuous variables
- Risk: A state of uncertainty where some possible outcomes have an undesired effect or significant loss.
- Measurement of Risk: A set of measured uncertainties where some possible outcomes are losses, and the magnitudes of those losses – this also includes loss functions over continuous variables.
There are other taxonomies of uncertainties and decisions that include a broader sense of uncertainty and how it should be approached from an ethics perspective:
For example, if you do not know whether it will rain tomorrow, then you have a state of uncertainty. If you apply probabilities to the possible outcomes using weather forecasts or even just a calibrated probability assessment
Calibrated probability assessment
Calibrated probability assessments are subjective probabilities assigned by individuals who have been trained to assess probabilities in a way that historically represents their uncertainty. In other words, when a calibrated person says they are "80% confident" in each of 100 predictions they...
, you have quantified the uncertainty. Suppose you quantify your uncertainty as a 90% chance of sunshine. If you are planning a major, costly, outdoor event for tomorrow then you have risk since there is a 10% chance of rain and rain would be undesirable. Furthermore, if this is a business event and you would lose $100,000 if it rains, then you have quantified the risk (a 10% chance of losing $100,000). These situations can be made even more realistic by quantifying light rain vs. heavy rain, the cost of delays vs. outright cancellation, etc.
Some may represent the risk in this example as the "expected opportunity loss" (EOL) or the chance of the loss multiplied by the amount of the loss (10% × $100,000 = $10,000). That is useful if the organizer of the event is "risk neutral," which most people are not. Most would be willing to pay a premium to avoid the loss. An insurance
Insurance
In law and economics, insurance is a form of risk management primarily used to hedge against the risk of a contingent, uncertain loss. Insurance is defined as the equitable transfer of the risk of a loss, from one entity to another, in exchange for payment. An insurer is a company selling the...
company, for example, would compute an EOL as a minimum for any insurance coverage, then add on to that other operating costs and profit. Since many people are willing to buy insurance for many reasons, then clearly the EOL alone is not the perceived value of avoiding the risk.
Quantitative uses of the terms uncertainty and risk are fairly consistent from fields such as probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, actuarial science
Actuarial science
Actuarial science is the discipline that applies mathematical and statistical methods to assess risk in the insurance and finance industries. Actuaries are professionals who are qualified in this field through education and experience...
, and information theory
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
. Some also create new terms without substantially changing the definitions of uncertainty or risk. For example, surprisal is a variation on uncertainty sometimes used in information theory
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
. But outside of the more mathematical uses of the term, usage may vary widely. In cognitive psychology
Cognitive psychology
Cognitive psychology is a subdiscipline of psychology exploring internal mental processes.It is the study of how people perceive, remember, think, speak, and solve problems.Cognitive psychology differs from previous psychological approaches in two key ways....
, uncertainty can be real, or just a matter of perception, such as expectation
Expectation
In the case of uncertainty, expectation is what is considered the most likely to happen. An expectation, which is a belief that is centered on the future, may or may not be realistic. A less advantageous result gives rise to the emotion of disappointment. If something happens that is not at all...
s, threats, etc.
Vagueness or ambiguity are sometimes described as "second order uncertainty," where there is uncertainty even about the definitions of uncertain states or outcomes. The difference here is that this uncertainty is about the human definitions and concepts, not an objective fact of nature. It has been argued that ambiguity, however, is always avoidable while uncertainty (of the "first order" kind) is not necessarily avoidable.
Uncertainty may be purely a consequence of a lack of knowledge of obtainable facts. That is, you may be uncertain about whether a new rocket design will work, but this uncertainty can be removed with further analysis and experimentation. At the subatomic level, however, uncertainty may be a fundamental and unavoidable property of the universe. In quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, the Heisenberg Uncertainty Principle puts limits on how much an observer can ever know about the position and velocity of a particle. This may not just be ignorance of potentially obtainable facts but that there is no fact to be found. There is some controversy in physics as to whether such uncertainty is an irreducible property of nature or if there are "hidden variables" that would describe the state of a particle even more exactly than Heisenberg's uncertainty principle allows.
Measurements
In metrology
Metrology
Metrology is the science of measurement. Metrology includes all theoretical and practical aspects of measurement. The word comes from Greek μέτρον , "measure" + "λόγος" , amongst others meaning "speech, oration, discourse, quote, study, calculation, reason"...
, physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, and engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
, the uncertainty or margin of error
Margin of error
The margin of error is a statistic expressing the amount of random sampling error in a survey's results. The larger the margin of error, the less faith one should have that the poll's reported results are close to the "true" figures; that is, the figures for the whole population...
of a measurement is stated by giving a range of values likely to enclose the true value. This may be denoted by error bar
Error bar
Error bars are a graphical representation of the variability of data and are used on graphs to indicate the error, or uncertainty in a reported measurement. They give a general idea of how accurate a measurement is, or conversely, how far from the reported value the true value might be...
s on a graph, or by the following notations:
- measured value ± uncertainty
- measured value
- measured value(uncertainty)
The middle notation is used when the error is not symmetrical about the value – for example
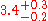. This can occur when using a logarithmic scale, for example. The latter "concise notation" is used for example by IUPAC in stating the atomic mass of elementsChemical element
A chemical element is a pure chemical substance consisting of one type of atom distinguished by its atomic number, which is the number of protons in its nucleus. Familiar examples of elements include carbon, oxygen, aluminum, iron, copper, gold, mercury, and lead.As of November 2011, 118 elements...
. There, the uncertainty given in parenthesis applies to the least significant figure(s) of x prior to the parenthesized value (ie. counting from rightmost digit to left). For instance, stands for , while stands for .
Often, the uncertainty of a measurement is found by repeating the measurement enough times to get a good estimate of the standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
of the values. Then, any single value has an uncertainty equal to the standard deviation. However, if the values are averaged, then the mean measurement value has a much smaller uncertainty, equal to the standard error
Standard error (statistics)
The standard error is the standard deviation of the sampling distribution of a statistic. The term may also be used to refer to an estimate of that standard deviation, derived from a particular sample used to compute the estimate....
of the mean, which is the standard deviation divided by the square root of the number of measurements.
When the uncertainty represents the standard error of the measurement, then about 68.2% of the time, the true value of the measured quantity falls within the stated uncertainty range. For example, it is likely that for 31.8% of the atomic mass values given on the list of elements by atomic mass, the true value lies outside of the stated range. If the width of the interval is doubled, then probably only 4.6% of the true values lie outside the doubled interval, and if the width is tripled, probably only 0.3% lie outside. These values follow from the properties of the normal distribution, and they apply only if the measurement process produces normally distributed errors. In that case, the quoted standard error
Standard error (statistics)
The standard error is the standard deviation of the sampling distribution of a statistic. The term may also be used to refer to an estimate of that standard deviation, derived from a particular sample used to compute the estimate....
s are easily converted to 68.3% ("one sigma"), 95.4% ("two sigma"), or 99.7% ("three sigma") confidence interval
Confidence interval
In statistics, a confidence interval is a particular kind of interval estimate of a population parameter and is used to indicate the reliability of an estimate. It is an observed interval , in principle different from sample to sample, that frequently includes the parameter of interest, if the...
s.
In this context, uncertainty depends on both the accuracy and precision
Accuracy and precision
In the fields of science, engineering, industry and statistics, the accuracy of a measurement system is the degree of closeness of measurements of a quantity to that quantity's actual value. The precision of a measurement system, also called reproducibility or repeatability, is the degree to which...
of the measurement instrument. The lower the accuracy and precision of an instrument, the larger the measurement uncertainty is. Notice that precision is often determined as the standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
of the repeated measures of a given value, namely using the same method described above to assess measurement uncertainty. However, this method is correct only when the instrument is accurate. When it is inaccurate, the uncertainty is larger than the standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
of the repeated measures, and it appears evident that the uncertainty does not depend only on instrumental precision.
Applications
- Investing in financial markets such as the stock market.
- Uncertainty or errorErrorThe word error entails different meanings and usages relative to how it is conceptually applied. The concrete meaning of the Latin word "error" is "wandering" or "straying". Unlike an illusion, an error or a mistake can sometimes be dispelled through knowledge...
is used in science and engineering notation. Numerical values should only be expressed to those digits that are physically meaningful, which are referred to as significant figuresSignificant figuresThe significant figures of a number are those digits that carry meaning contributing to its precision. This includes all digits except:...
. Uncertainty is involved in every measurement, such as measuring a distance, a temperature, etc., the degree depending upon the instrument or technique used to make the measurement. Similarly, uncertainty is propagated through calculations so that the calculated value has some degree of uncertainty depending upon the uncertainties of the measured values and the equation used in the calculation. - Uncertainty is designed into gameGameA game is structured playing, usually undertaken for enjoyment and sometimes used as an educational tool. Games are distinct from work, which is usually carried out for remuneration, and from art, which is more often an expression of aesthetic or ideological elements...
s, most notably in gamblingGamblingGambling is the wagering of money or something of material value on an event with an uncertain outcome with the primary intent of winning additional money and/or material goods...
, where chanceProbabilityProbability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
is central to play. - In scientific modellingScientific modellingScientific modelling is the process of generating abstract, conceptual, graphical and/or mathematical models. Science offers a growing collection of methods, techniques and theory about all kinds of specialized scientific modelling...
, in which the prediction of future events should be understood to have a range of expected values. - In physicsPhysicsPhysics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the Heisenberg uncertainty principleUncertainty principleIn quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
forms the basis of modern quantum mechanicsQuantum mechanicsQuantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. - In weather forecastingMeteorologyMeteorology is the interdisciplinary scientific study of the atmosphere. Studies in the field stretch back millennia, though significant progress in meteorology did not occur until the 18th century. The 19th century saw breakthroughs occur after observing networks developed across several countries...
it is now commonplace to include data on the degree of uncertainty in a weather forecast. - Uncertainty is often an important factor in economicsEconomicsEconomics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
. According to economist Frank KnightFrank KnightFrank Hyneman Knight was an American economist who spent most of his career at the University of Chicago, where he became one of the founders of the Chicago school. Nobel laureates James M. Buchanan, Milton Friedman and George Stigler were all students of Knight at Chicago. Knight supervised...
, it is different from riskRiskRisk is the potential that a chosen action or activity will lead to a loss . The notion implies that a choice having an influence on the outcome exists . Potential losses themselves may also be called "risks"...
, where there is a specific probabilityProbabilityProbability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
assigned to each outcome (as when flipping a fair coin). Uncertainty involves a situation that has unknown probabilities, while the estimated probabilities of possible outcomes need not add to unity. - In entrepreneurshipEntrepreneurshipEntrepreneurship is the act of being an entrepreneur, which can be defined as "one who undertakes innovations, finance and business acumen in an effort to transform innovations into economic goods". This may result in new organizations or may be part of revitalizing mature organizations in response...
: New products, services, firms and even markets are often created in the absence of probability estimates. According to entrepreneurship research, expert entrepreneurs predominantly use experience based heuristics called effectuationEffectuationEffectuation is a set of decision-making principles expert entrepreneurs are observed to employ in situations of uncertainty. The alternative to effectuation is causality, which describes decision-making heuristics rooted in prediction....
(as opposed to causalityCausalityCausality is the relationship between an event and a second event , where the second event is understood as a consequence of the first....
) to overcome uncertainty. - In risk assessmentRisk assessmentRisk assessment is a step in a risk management procedure. Risk assessment is the determination of quantitative or qualitative value of risk related to a concrete situation and a recognized threat...
and risk managementRisk managementRisk management is the identification, assessment, and prioritization of risks followed by coordinated and economical application of resources to minimize, monitor, and control the probability and/or impact of unfortunate events or to maximize the realization of opportunities...
. In metrology
MetrologyMetrology is the science of measurement. Metrology includes all theoretical and practical aspects of measurement. The word comes from Greek μέτρον , "measure" + "λόγος" , amongst others meaning "speech, oration, discourse, quote, study, calculation, reason"...
, measurement uncertaintyMeasurement uncertaintyIn metrology, measurement uncertainty is a non-negative parameter characterizing the dispersion of the values attributed to a measured quantity. The uncertainty has a probabilistic basis and reflects incomplete knowledge of the quantity. All measurements are subject to uncertainty and a measured...
is a central concept quantifying the dispersion one may reasonably attribute to a measurement result. Such an uncertainty can also be referred to as a measurement errorErrorThe word error entails different meanings and usages relative to how it is conceptually applied. The concrete meaning of the Latin word "error" is "wandering" or "straying". Unlike an illusion, an error or a mistake can sometimes be dispelled through knowledge...
. In daily life, measurement uncertainty is often implicit ("He is 6 feet tall" give or take a few inches), while for any serious use an explicit statement of the measurement uncertainty is necessary. The expected measurement uncertainty of many measuring instruments (scales, oscilloscopes, force gages, rulers, thermometers, etc.) is often stated in the manufacturer's specification.
The most commonly used procedure for calculating measurement uncertainty is described in the Guide to the Expression of Uncertainty in Measurement (often referred to as "the GUM") published by ISO. A derived work is for example the National Institute for Standards and Technology (NIST) publication NIST Technical Note 1297 "Guidelines for Evaluating and Expressing the Uncertainty of NIST Measurement Results" and the Eurachem/Citac publication "Quantifying Uncertainty in Analytical Measurement" (available at the Eurachem homepage). The uncertainty of the result of a measurement generally consists of several components. The components are regarded as random variables, and may be grouped into two categories according to the method used to estimate their numerical values:
- Type A, those evaluated by statistical methods
- Type B, those evaluated by other means, e.g., by assigning a probability distribution
By propagating the varianceVarianceIn probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
s of the components through a function relating the components to the measurement result, the combined measurement uncertainty is given as the square root of the resulting variance. The simplest form is the standard deviationStandard deviationStandard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
of a repeated observation.
- Uncertainty has been a common theme in art, both as a thematic device (see, for example, the indecision of HamletHamletThe Tragical History of Hamlet, Prince of Denmark, or more simply Hamlet, is a tragedy by William Shakespeare, believed to have been written between 1599 and 1601...
), and as a quandary for the artist (such as Martin CreedMartin CreedMartin Creed is an artist and musician. He won the Turner Prize in 2001 for Work No. 227: the lights going on and off, which was an empty room in which the lights went on and off.-Life and work :...
's difficulty with deciding what artworks to make).
External links
- Measurement Uncertainties in Science and Technology, Springer 2005
- Proposal for a New Error Calculus
- Estimation of Measurement Uncertainties — an Alternative to the ISO Guide
- Bibliography of Papers Regarding Measurement Uncertainty
- Guidelines for Evaluating and Expressing the Uncertainty of NIST Measurement Results
- Strategic Engineering: Designing Systems and Products under Uncertainty (MIT Research Group)
- Research results regarding uncertainty models, uncertainty quantification, and uncertainty processing
- Decision tree to choose an uncertainty method for hydrological and hydraulic modelling, Choosing an uncertainty analysis for flood modelling.
- Decision Analysis in Health Care George Mason University online course offering lectures and tools for modeling and mitigating uncertainty in health care scenarios.
- Technological uncertainty - an example
- Uri Weiss, The Regressive Effect of Legal Uncertainty, law.bepress.com
- NUSAP.net educational website dedicated to coping with uncertainty and quality in science for policy, for all actors involved in the science policy interface.
- Understanding Uncertainty site from Cambridge's Winton programme