
Measurement uncertainty
Encyclopedia
In metrology
, measurement uncertainty is a non-negative parameter characterizing the dispersion
of the values attributed to a measured quantity. The uncertainty has a probabilistic basis and reflects incomplete knowledge of the quantity. All measurements are subject to uncertainty and a measured value is only complete if it is accompanied by a statement of the associated uncertainty. Fractional uncertainty is the measurement uncertainty divided by the measured value.
Codex has guidelines on Measurement Uncertainty, CAC/GL 54-2004.
of interest - a measurand. For example, the measurand might be the volume
of a vessel, the potential difference between the terminals of a battery, or the mass concentration of lead in a flask of water.
No measurement is exact. When a quantity is measured, the outcome depends on the measuring system, the measurement procedure, the skill of the operator, the environment, and other effects. Even if the quantity were to be measured several times, in the same way and in the same circumstances, a different measured value would in general be obtained each time, assuming that the measuring system has sufficient resolution to distinguish between the values.
The dispersion of the measured values would relate to how well the measurement is made.
Their average
would provide an estimate of the true value of the quantity that generally would be more reliable than an individual measured value.
The dispersion and the number of measured values would provide information relating to the average value as an estimate of the true value.
However, this information would not generally be adequate.
The measuring system may provide measured values that are not dispersed about the true value, but about some value offset from it. Take a domestic bathroom scale. Suppose it is not set to show zero when there is nobody on the scale, but to show some value offset from zero. Then, no matter how many times the person's mass were re-measured, the effect of this offset would be inherently present in the average of the values.
and random uncertainty
.
A systematic error (an estimate of which is known as a measurement bias) is associated with the fact that a measured value contains an offset. In general, a systematic error, regarded as a quantity, is a component of error that remains constant or depends in a specific manner on some other quantity.
A random uncertainty is associated with the fact that when a measurement is repeated it will generally provide a measured value that is different from the previous value. It is random in that the next measured value cannot be predicted exactly from previous such values. (If a prediction were possible, allowance for the effect could be made.)
In general, there can be a number of contributions to each type of error.
The GUM provides a way to express the perceived quality of the result of a measurement. Rather than express the result by providing a best estimate of the measurand along with information about systematic and random error values (in the form of an "error analysis"), the GUM approach is to express the result of a measurement as a best estimate of the measurand along with an associated measurement uncertainty.
One of the basic premises of the GUM approach is that it is possible to characterize the quality of a measurement by accounting for both systematic and random errors on a comparable footing, and a method is provided for doing that. This method refines the information previously provided in an "error analysis", and puts it on a probabilistic basis through the concept of measurement uncertainty.
Another basic premise of the GUM approach is that it is not possible to state how well the true value of the measurand is known, but only how well it is believed to be known. Measurement uncertainty can therefore be described as a measure of how well one believes one knows the true value of the measurand. This uncertainty reflects the incomplete knowledge of the measurand.
The notion of "belief" is an important one, since it moves metrology into a realm where results of measurement need to be considered and quantified in terms of probabilities
that express degrees of belief.
of the person on the scale. The particular relationship between extension and mass is determined by the calibration
of the scale. A measurement model
converts a quantity value into the corresponding value of the measurand.
There are many types of measurement in practice and therefore many models. A simple measurement model (for example for a scale, where the mass is proportional to the extension of the spring) might be sufficient for everyday domestic use. Alternatively, a more sophisticated model of a weighing, involving additional effects such as air buoyancy
, is capable of delivering better results for industrial or scientific purposes. In general there are often several different quantities, for example temperature
, humidity
and displacement
, that contribute to the definition of the measurand, and that need to be measured.
Correction terms should be included in the measurement model when the conditions of measurement are not exactly as stipulated. These terms correspond to systematic errors. Given an estimate of a correction term, the relevant quantity should be corrected by this estimate. There will be an uncertainty associated with the estimate, even if the estimate is zero, as is often the case. Instances of systematic errors arise in height measurement, when the alignment of the measuring instrument is not perfectly vertical, and the ambient temperature is different from that prescribed. Neither the alignment of the instrument nor the ambient temperature is specified exactly, but information concerning these effects is available, for example the lack of alignment is at most 0.001° and the ambient temperature at the time of measurement differs from that stipulated by at most 2 °C.
As well as raw data representing measured values, there is another form of data that is frequently needed in a measurement model. Some such data relate to quantities representing physical constant
s, each of which is known imperfectly. Examples are material constants such as modulus of elasticity
and specific heat. There are often other relevant data given in reference books, calibration certificates, etc., regarded as estimates of further quantities.
The items required by a measurement model to define a measurand are known as input quantities in a measurement model. The model is often referred to as a functional relationship. The output quantity in a measurement model is the measurand.
Formally, the output quantity, denoted by , about which information is required, is often related to input quantities, denoted by
, about which information is required, is often related to input quantities, denoted by 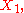 ...
... 
 , about which information is available, by a measurement model in the form of a measurement function
, about which information is available, by a measurement model in the form of a measurement function
 ...
... 
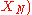 .
.
A general expression for a measurement model is

 ...
... 
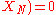 .
.
It is taken that a procedure exists for calculating given
given  ...
... 
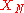 , and that
, and that  is uniquely
is uniquely
defined by this equation.
 ...
... 
 are unknown.
are unknown.
In the GUM approach, ...
... 
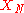 are characterized by probability distribution
are characterized by probability distribution
s and treated mathematically as random variable
s.
These distributions describe the respective probabilities of their true values lying in different intervals, and are assigned based on available knowledge concerning ...
... 
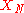 .
.
Sometimes, some or all of are interrelated and the relevant distributions, which are known as joint, apply to these quantities taken together.
Consider estimates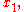 ...
... 
 , respectively, of the input quantities
, respectively, of the input quantities  ...
... 
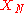 , obtained from certificates and reports, manufacturers' specifications, the analysis of measurement data, and so on.
, obtained from certificates and reports, manufacturers' specifications, the analysis of measurement data, and so on.
The probability distributions characterizing ...
... 
 are chosen such that the estimates
are chosen such that the estimates 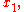 ...
... 
 , respectively, are the expectations
, respectively, are the expectations
of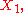 ...
... 
 .
.
Moreover, for the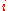 th input quantity, consider a so-called standard uncertainty, given the symbol
th input quantity, consider a so-called standard uncertainty, given the symbol 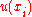 , defined as the standard deviation
, defined as the standard deviation
of the input quantity .
.
This standard uncertainty is said to be associated with the (corresponding) estimate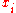 .
.
The estimate is best in the sense that
is best in the sense that  is smaller than the expected squared difference of
is smaller than the expected squared difference of 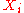 from any other value.
from any other value.
The use of available knowledge to establish a probability distribution to characterize each quantity of interest applies to the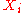 and also to
and also to  .
.
In the latter case, the characterizing probability distribution for is determined by the measurement model together with the probability distributions for the
is determined by the measurement model together with the probability distributions for the 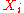 .
.
The determination of the probability distribution for from this information is known as the propagation of distributions.
from this information is known as the propagation of distributions.
The figure below depicts a measurement function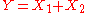 in the case where
in the case where  and
and 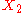 are each characterized by a (different) rectangular, or uniform
are each characterized by a (different) rectangular, or uniform
, probability distribution.
 has a symmetric trapezoidal probability distribution in this case.
has a symmetric trapezoidal probability distribution in this case.
Once the input quantities ...
... 
 have been characterized by appropriate probability distributions, and the measurement model has been developed, the probability distribution for the measurand
have been characterized by appropriate probability distributions, and the measurement model has been developed, the probability distribution for the measurand  is fully specified in terms of this information. In particular, the expectation of
is fully specified in terms of this information. In particular, the expectation of  is used as the estimate of
is used as the estimate of  , and the standard deviation of
, and the standard deviation of  as the standard uncertainty associated with this estimate.
as the standard uncertainty associated with this estimate.
Often an interval containing with a specified probability is required. Such an interval, a coverage interval, can be deduced from the probability distribution for
with a specified probability is required. Such an interval, a coverage interval, can be deduced from the probability distribution for  . The specified probability is known as the coverage probability. For a given coverage probability, there is more than one coverage interval. The probabilistically symmetric coverage interval is an interval for which the probabilities (summing to one minus the coverage probability) of a value to the left and the right of the interval are equal. The shortest coverage interval is an interval for which the length is least over all coverage intervals having the same coverage probability.
. The specified probability is known as the coverage probability. For a given coverage probability, there is more than one coverage interval. The probabilistically symmetric coverage interval is an interval for which the probabilities (summing to one minus the coverage probability) of a value to the left and the right of the interval are equal. The shortest coverage interval is an interval for which the length is least over all coverage intervals having the same coverage probability.
Prior knowledge about the true value of the output quantity can also be considered. For the domestic bathroom scale, the fact that the person's mass is positive, and that it is the mass of a person, rather than that of a motor car, that is being measured, both constitute prior knowledge about the possible values of the measurand in this example. Such additional information can be used to provide a probability distribution for
can also be considered. For the domestic bathroom scale, the fact that the person's mass is positive, and that it is the mass of a person, rather than that of a motor car, that is being measured, both constitute prior knowledge about the possible values of the measurand in this example. Such additional information can be used to provide a probability distribution for  that can give a smaller standard deviation for
that can give a smaller standard deviation for  and hence a smaller standard uncertainty associated with the estimate of
and hence a smaller standard uncertainty associated with the estimate of  .
.
 is inferred from repeated measured values (Type A evaluation of uncertainty), or scientific judgement or other information concerning the possible values of the quantity (Type B evaluation of uncertainty).
is inferred from repeated measured values (Type A evaluation of uncertainty), or scientific judgement or other information concerning the possible values of the quantity (Type B evaluation of uncertainty).
In Type A evaluations of measurement uncertainty, the assumption is often made that the distribution best describing an input quantity given repeated measured values of it (obtained independently) is a Gaussian distribution.
given repeated measured values of it (obtained independently) is a Gaussian distribution.
 then has expectation equal to the average measured value and standard deviation equal to the standard deviation of the average.
then has expectation equal to the average measured value and standard deviation equal to the standard deviation of the average.
When the uncertainty is evaluated from a small number of measured values (regarded as instances of a quantity characterized by a Gaussian distribution), the corresponding distribution can be taken as a -distribution.
-distribution.
Other considerations apply when the measured values are not obtained independently.
For a Type B evaluation of uncertainty, often the only available information is that lies in a specified interval
lies in a specified interval
[
 ].
].
In such a case, knowledge of the quantity can be characterized by a rectangular probability distribution
with limits and
and  .
.
If different information were available, a probability distribution consistent with that information would be used.
 ...
... 
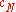 describe how the estimate
describe how the estimate 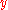 of
of  would be influenced by small changes in the estimates
would be influenced by small changes in the estimates 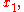 ...
...
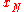 of the input quantities
of the input quantities  ...
... 
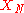 .
.
For the measurement function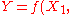 ...
... 
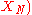 , the sensitivity coefficient
, the sensitivity coefficient 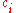 equals the partial derivative
equals the partial derivative
of first order of with respect to
with respect to 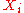 evaluated at
evaluated at 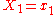 ,
,  , etc.
, etc.
For a linear
measurement function
 ,
,
with ...
... 
 independent, a change in
independent, a change in  equal to
equal to  would give a change
would give a change  in
in 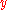 .
.
This statement would generally be approximate for measurement functions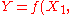 ...
... 
 .
.
The relative magnitudes of the terms are useful in assessing the respective contributions from the input quantities to the standard uncertainty
are useful in assessing the respective contributions from the input quantities to the standard uncertainty 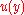 associated with
associated with 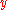 .
.
The standard uncertainty associated with the estimate
associated with the estimate 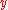 of the output quantity
of the output quantity  is not given by the sum of the
is not given by the sum of the 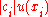 , but these terms combined in quadrature, namely by (an expression that is generally approximate for measurement functions
, but these terms combined in quadrature, namely by (an expression that is generally approximate for measurement functions 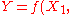 ...
... 
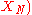 )
)
 ,
,
which is known as the law of propagation of uncertainty.
When the input quantities contain dependencies, the above formula is augmented by terms containing covariance
contain dependencies, the above formula is augmented by terms containing covariance
s, which may increase or decrease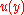 .
.
The formulation stage constitutes
The calculation stage consists of propagating the probability distributions for the input quantities through the measurement model to obtain the probability distribution for the output quantity , and summarizing by using this distribution to obtain
, and summarizing by using this distribution to obtain
The propagation stage of uncertainty evaluation is known as the propagation of distributions, various approaches for which are available, including
For any particular uncertainty evaluation problem, approach 1), 2) or 3) (or some other approach) is used, 1) being generally approximate, 2) exact, and 3) providing a solution with a numerical accuracy that can be controlled.
, was created
by the seven international organizations that had originally in 1993 prepared the "Guide to the expression of uncertainty in measurement" (GUM) and the "International vocabulary of metrology – basic and general concepts and associated terms" (VIM). The JCGM assumed responsibility for these two documents from the ISO Technical
Advisory Group 4 (TAG4).
The Joint Committee is formed by the BIPM with the International Electrotechnical Commission (IEC), the International Federation of Clinical Chemistry and Laboratory Medicine (IFCC), the International Laboratory Accreditation Cooperation (ILAC), the International Organization for Standardization (ISO), the International Union of Pure and Applied Chemistry (IUPAC), the International Union of Pure and Applied Physics (IUPAP), and the International Organization of Legal Metrology (OIML).
JCGM has two Working Groups. Working Group 1, "Expression of uncertainty in measurement", has the task to promote the use of the GUM and to prepare Supplements and other documents for its broad application. Working Group 2, "Working Group on International vocabulary of basic and general terms in metrology (VIM)", has the task to revise and promote the use of the VIM. For further information on the activity of the JCGM, see www.bipm.org.
Revision by Working Group 1 of the GUM itself has started in parallel with work on preparing documents in a series of JCGM documents under the generic heading Evaluation of
measurement data. The parts in the series are
that random variables are proper mathematical models for uncertain quantities and simple
probability distributions are sufficient for representing all forms of measurement uncertainties.
In some situations, however, a mathematical interval
rather than a probability
distribution might be a better model of uncertainty. This may include situations involving periodic measurements,
binned
data values, censoring
, detection limits, or
plus-minus ranges of measurements where no particular probability distribution seems justified or
where one cannot assume that the errors among individual measuresments are completely independent.
A more robust
representation of measurement uncertainty in such cases can be fashioned from intervals.
An interval [a,b] is different from a rectangular or uniform probability distribution over the same range in that the
latter suggests that the true value lies inside the right half of the range [(a+b)/2, b] with
probability one half, and within any subinterval of [a,b] with probability equal to the width of the subinterval divided by b–a.
The interval makes no such claims, except simply that the measurement lies somewhere within the interval.
Distributions of such measurement intervals can be summarized as
probability box
es and Dempster-Shafer structures
over the real
numbers, which incorporate both aleatoric and epistemic uncertainties
.
Metrology
Metrology is the science of measurement. Metrology includes all theoretical and practical aspects of measurement. The word comes from Greek μέτρον , "measure" + "λόγος" , amongst others meaning "speech, oration, discourse, quote, study, calculation, reason"...
, measurement uncertainty is a non-negative parameter characterizing the dispersion
Statistical dispersion
In statistics, statistical dispersion is variability or spread in a variable or a probability distribution...
of the values attributed to a measured quantity. The uncertainty has a probabilistic basis and reflects incomplete knowledge of the quantity. All measurements are subject to uncertainty and a measured value is only complete if it is accompanied by a statement of the associated uncertainty. Fractional uncertainty is the measurement uncertainty divided by the measured value.
Codex has guidelines on Measurement Uncertainty, CAC/GL 54-2004.
Background
The purpose of measurement is to provide information about a quantityQuantity
Quantity is a property that can exist as a magnitude or multitude. Quantities can be compared in terms of "more" or "less" or "equal", or by assigning a numerical value in terms of a unit of measurement. Quantity is among the basic classes of things along with quality, substance, change, and relation...
of interest - a measurand. For example, the measurand might be the volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
of a vessel, the potential difference between the terminals of a battery, or the mass concentration of lead in a flask of water.
No measurement is exact. When a quantity is measured, the outcome depends on the measuring system, the measurement procedure, the skill of the operator, the environment, and other effects. Even if the quantity were to be measured several times, in the same way and in the same circumstances, a different measured value would in general be obtained each time, assuming that the measuring system has sufficient resolution to distinguish between the values.
The dispersion of the measured values would relate to how well the measurement is made.
Their average
Average
In mathematics, an average, or central tendency of a data set is a measure of the "middle" value of the data set. Average is one form of central tendency. Not all central tendencies should be considered definitions of average....
would provide an estimate of the true value of the quantity that generally would be more reliable than an individual measured value.
The dispersion and the number of measured values would provide information relating to the average value as an estimate of the true value.
However, this information would not generally be adequate.
The measuring system may provide measured values that are not dispersed about the true value, but about some value offset from it. Take a domestic bathroom scale. Suppose it is not set to show zero when there is nobody on the scale, but to show some value offset from zero. Then, no matter how many times the person's mass were re-measured, the effect of this offset would be inherently present in the average of the values.
Random uncertainties and systematic errors
There are two types of measurement faults, systematic errorSystematic error
Systematic errors are biases in measurement which lead to the situation where the mean of many separate measurements differs significantly from the actual value of the measured attribute. All measurements are prone to systematic errors, often of several different types...
and random uncertainty
Random error
Random errors are errors in measurement that lead to measurable values being inconsistent when repeated measures of a constant attribute or quantity are taken...
.
A systematic error (an estimate of which is known as a measurement bias) is associated with the fact that a measured value contains an offset. In general, a systematic error, regarded as a quantity, is a component of error that remains constant or depends in a specific manner on some other quantity.
A random uncertainty is associated with the fact that when a measurement is repeated it will generally provide a measured value that is different from the previous value. It is random in that the next measured value cannot be predicted exactly from previous such values. (If a prediction were possible, allowance for the effect could be made.)
In general, there can be a number of contributions to each type of error.
GUM approach
The Guide to the Expression of Uncertainty in Measurement (GUM) is a document published by the JCGM that establishes general rules for evaluating and expressing uncertainty in measurement.The GUM provides a way to express the perceived quality of the result of a measurement. Rather than express the result by providing a best estimate of the measurand along with information about systematic and random error values (in the form of an "error analysis"), the GUM approach is to express the result of a measurement as a best estimate of the measurand along with an associated measurement uncertainty.
One of the basic premises of the GUM approach is that it is possible to characterize the quality of a measurement by accounting for both systematic and random errors on a comparable footing, and a method is provided for doing that. This method refines the information previously provided in an "error analysis", and puts it on a probabilistic basis through the concept of measurement uncertainty.
Another basic premise of the GUM approach is that it is not possible to state how well the true value of the measurand is known, but only how well it is believed to be known. Measurement uncertainty can therefore be described as a measure of how well one believes one knows the true value of the measurand. This uncertainty reflects the incomplete knowledge of the measurand.
The notion of "belief" is an important one, since it moves metrology into a realm where results of measurement need to be considered and quantified in terms of probabilities
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
that express degrees of belief.
Measurement model
The above discussion concerns the direct measurement of a quantity, which incidentally occurs rarely. For example, the bathroom scale may convert a measured extension of a spring into an estimate of the measurand, the massMass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
of the person on the scale. The particular relationship between extension and mass is determined by the calibration
Calibration
Calibration is a comparison between measurements – one of known magnitude or correctness made or set with one device and another measurement made in as similar a way as possible with a second device....
of the scale. A measurement model
Mathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
converts a quantity value into the corresponding value of the measurand.
There are many types of measurement in practice and therefore many models. A simple measurement model (for example for a scale, where the mass is proportional to the extension of the spring) might be sufficient for everyday domestic use. Alternatively, a more sophisticated model of a weighing, involving additional effects such as air buoyancy
Buoyancy
In physics, buoyancy is a force exerted by a fluid that opposes an object's weight. In a column of fluid, pressure increases with depth as a result of the weight of the overlying fluid. Thus a column of fluid, or an object submerged in the fluid, experiences greater pressure at the bottom of the...
, is capable of delivering better results for industrial or scientific purposes. In general there are often several different quantities, for example temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
, humidity
Humidity
Humidity is a term for the amount of water vapor in the air, and can refer to any one of several measurements of humidity. Formally, humid air is not "moist air" but a mixture of water vapor and other constituents of air, and humidity is defined in terms of the water content of this mixture,...
and displacement
Displacement (vector)
A displacement is the shortest distance from the initial to the final position of a point P. Thus, it is the length of an imaginary straight path, typically distinct from the path actually travelled by P...
, that contribute to the definition of the measurand, and that need to be measured.
Correction terms should be included in the measurement model when the conditions of measurement are not exactly as stipulated. These terms correspond to systematic errors. Given an estimate of a correction term, the relevant quantity should be corrected by this estimate. There will be an uncertainty associated with the estimate, even if the estimate is zero, as is often the case. Instances of systematic errors arise in height measurement, when the alignment of the measuring instrument is not perfectly vertical, and the ambient temperature is different from that prescribed. Neither the alignment of the instrument nor the ambient temperature is specified exactly, but information concerning these effects is available, for example the lack of alignment is at most 0.001° and the ambient temperature at the time of measurement differs from that stipulated by at most 2 °C.
As well as raw data representing measured values, there is another form of data that is frequently needed in a measurement model. Some such data relate to quantities representing physical constant
Physical constant
A physical constant is a physical quantity that is generally believed to be both universal in nature and constant in time. It can be contrasted with a mathematical constant, which is a fixed numerical value but does not directly involve any physical measurement.There are many physical constants in...
s, each of which is known imperfectly. Examples are material constants such as modulus of elasticity
Elastic modulus
An elastic modulus, or modulus of elasticity, is the mathematical description of an object or substance's tendency to be deformed elastically when a force is applied to it...
and specific heat. There are often other relevant data given in reference books, calibration certificates, etc., regarded as estimates of further quantities.
The items required by a measurement model to define a measurand are known as input quantities in a measurement model. The model is often referred to as a functional relationship. The output quantity in a measurement model is the measurand.
Formally, the output quantity, denoted by
 , about which information is required, is often related to input quantities, denoted by
, about which information is required, is often related to input quantities, denoted by 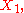 ...
... 
 , about which information is available, by a measurement model in the form of a measurement function
, about which information is available, by a measurement model in the form of a measurement function ...
... 
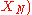 .
.A general expression for a measurement model is

 ...
... 
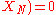 .
.It is taken that a procedure exists for calculating
 given
given  ...
... 
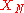 , and that
, and that  is uniquely
is uniquelydefined by this equation.
Propagation of distributions
The true values of the input quantities ...
... 
 are unknown.
are unknown.In the GUM approach,
 ...
... 
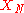 are characterized by probability distribution
are characterized by probability distributionProbability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s and treated mathematically as random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s.
These distributions describe the respective probabilities of their true values lying in different intervals, and are assigned based on available knowledge concerning
 ...
... 
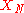 .
.Sometimes, some or all of are interrelated and the relevant distributions, which are known as joint, apply to these quantities taken together.
Consider estimates
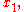 ...
... 
 , respectively, of the input quantities
, respectively, of the input quantities  ...
... 
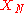 , obtained from certificates and reports, manufacturers' specifications, the analysis of measurement data, and so on.
, obtained from certificates and reports, manufacturers' specifications, the analysis of measurement data, and so on.The probability distributions characterizing
 ...
... 
 are chosen such that the estimates
are chosen such that the estimates 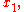 ...
... 
 , respectively, are the expectations
, respectively, are the expectationsExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of
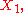 ...
... 
 .
.Moreover, for the
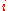 th input quantity, consider a so-called standard uncertainty, given the symbol
th input quantity, consider a so-called standard uncertainty, given the symbol 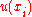 , defined as the standard deviation
, defined as the standard deviationStandard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
of the input quantity
 .
.This standard uncertainty is said to be associated with the (corresponding) estimate
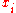 .
.The estimate
 is best in the sense that
is best in the sense that  is smaller than the expected squared difference of
is smaller than the expected squared difference of 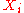 from any other value.
from any other value.The use of available knowledge to establish a probability distribution to characterize each quantity of interest applies to the
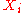 and also to
and also to  .
.In the latter case, the characterizing probability distribution for
 is determined by the measurement model together with the probability distributions for the
is determined by the measurement model together with the probability distributions for the 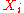 .
.The determination of the probability distribution for
 from this information is known as the propagation of distributions.
from this information is known as the propagation of distributions.The figure below depicts a measurement function
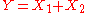 in the case where
in the case where  and
and 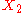 are each characterized by a (different) rectangular, or uniform
are each characterized by a (different) rectangular, or uniformUniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
, probability distribution.
 has a symmetric trapezoidal probability distribution in this case.
has a symmetric trapezoidal probability distribution in this case.Once the input quantities
 ...
... 
 have been characterized by appropriate probability distributions, and the measurement model has been developed, the probability distribution for the measurand
have been characterized by appropriate probability distributions, and the measurement model has been developed, the probability distribution for the measurand  is fully specified in terms of this information. In particular, the expectation of
is fully specified in terms of this information. In particular, the expectation of  is used as the estimate of
is used as the estimate of  , and the standard deviation of
, and the standard deviation of  as the standard uncertainty associated with this estimate.
as the standard uncertainty associated with this estimate.Often an interval containing
 with a specified probability is required. Such an interval, a coverage interval, can be deduced from the probability distribution for
with a specified probability is required. Such an interval, a coverage interval, can be deduced from the probability distribution for  . The specified probability is known as the coverage probability. For a given coverage probability, there is more than one coverage interval. The probabilistically symmetric coverage interval is an interval for which the probabilities (summing to one minus the coverage probability) of a value to the left and the right of the interval are equal. The shortest coverage interval is an interval for which the length is least over all coverage intervals having the same coverage probability.
. The specified probability is known as the coverage probability. For a given coverage probability, there is more than one coverage interval. The probabilistically symmetric coverage interval is an interval for which the probabilities (summing to one minus the coverage probability) of a value to the left and the right of the interval are equal. The shortest coverage interval is an interval for which the length is least over all coverage intervals having the same coverage probability.Prior knowledge about the true value of the output quantity
 can also be considered. For the domestic bathroom scale, the fact that the person's mass is positive, and that it is the mass of a person, rather than that of a motor car, that is being measured, both constitute prior knowledge about the possible values of the measurand in this example. Such additional information can be used to provide a probability distribution for
can also be considered. For the domestic bathroom scale, the fact that the person's mass is positive, and that it is the mass of a person, rather than that of a motor car, that is being measured, both constitute prior knowledge about the possible values of the measurand in this example. Such additional information can be used to provide a probability distribution for  that can give a smaller standard deviation for
that can give a smaller standard deviation for  and hence a smaller standard uncertainty associated with the estimate of
and hence a smaller standard uncertainty associated with the estimate of  .
.Type A and Type B evaluation of uncertainty
Knowledge about an input quantity is inferred from repeated measured values (Type A evaluation of uncertainty), or scientific judgement or other information concerning the possible values of the quantity (Type B evaluation of uncertainty).
is inferred from repeated measured values (Type A evaluation of uncertainty), or scientific judgement or other information concerning the possible values of the quantity (Type B evaluation of uncertainty).In Type A evaluations of measurement uncertainty, the assumption is often made that the distribution best describing an input quantity
 given repeated measured values of it (obtained independently) is a Gaussian distribution.
given repeated measured values of it (obtained independently) is a Gaussian distribution. then has expectation equal to the average measured value and standard deviation equal to the standard deviation of the average.
then has expectation equal to the average measured value and standard deviation equal to the standard deviation of the average.When the uncertainty is evaluated from a small number of measured values (regarded as instances of a quantity characterized by a Gaussian distribution), the corresponding distribution can be taken as a
 -distribution.
-distribution.Other considerations apply when the measured values are not obtained independently.
For a Type B evaluation of uncertainty, often the only available information is that
 lies in a specified interval
lies in a specified intervalInterval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
[

 ].
].In such a case, knowledge of the quantity can be characterized by a rectangular probability distribution
Uniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
with limits
 and
and  .
.If different information were available, a probability distribution consistent with that information would be used.
Sensitivity coefficients
Sensitivity coefficients ...
... 
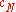 describe how the estimate
describe how the estimate 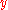 of
of  would be influenced by small changes in the estimates
would be influenced by small changes in the estimates 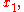 ...
...
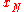 of the input quantities
of the input quantities  ...
... 
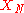 .
.For the measurement function
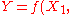 ...
... 
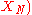 , the sensitivity coefficient
, the sensitivity coefficient 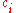 equals the partial derivative
equals the partial derivativePartial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
of first order of
 with respect to
with respect to 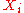 evaluated at
evaluated at 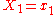 ,
,  , etc.
, etc.For a linear
Linear function
In mathematics, the term linear function can refer to either of two different but related concepts:* a first-degree polynomial function of one variable;* a map between two vector spaces that preserves vector addition and scalar multiplication....
measurement function
 ,
,with
 ...
... 
 independent, a change in
independent, a change in  equal to
equal to  would give a change
would give a change  in
in 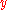 .
.This statement would generally be approximate for measurement functions
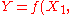 ...
... 
 .
.The relative magnitudes of the terms
 are useful in assessing the respective contributions from the input quantities to the standard uncertainty
are useful in assessing the respective contributions from the input quantities to the standard uncertainty 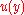 associated with
associated with 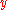 .
.The standard uncertainty
 associated with the estimate
associated with the estimate 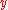 of the output quantity
of the output quantity  is not given by the sum of the
is not given by the sum of the 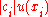 , but these terms combined in quadrature, namely by (an expression that is generally approximate for measurement functions
, but these terms combined in quadrature, namely by (an expression that is generally approximate for measurement functions 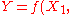 ...
... 
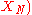 )
) ,
,which is known as the law of propagation of uncertainty.
When the input quantities
 contain dependencies, the above formula is augmented by terms containing covariance
contain dependencies, the above formula is augmented by terms containing covarianceCovariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
s, which may increase or decrease
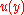 .
.Stages of uncertainty evaluation
The main stages of uncertainty evaluation constitute formulation and calculation, the latter consisting of propagation and summarizing.The formulation stage constitutes
- defining the output quantity
 (the measurand),
(the measurand), - identifying the input quantities on which
 depends,
depends, - developing a measurement model relating
 to the input quantities, and
to the input quantities, and - on the basis of available knowledge, assigning probability distributions — Gaussian, rectangular, etc. — to the input quantities (or a joint probability distribution to those input quantities that are not independent).
The calculation stage consists of propagating the probability distributions for the input quantities through the measurement model to obtain the probability distribution for the output quantity
 , and summarizing by using this distribution to obtain
, and summarizing by using this distribution to obtain
- the expectation of
 , taken as an estimate
, taken as an estimate 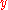 of
of  ,
, - the standard deviation of
 , taken as the standard uncertainty
, taken as the standard uncertainty 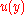 associated with
associated with 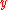 , and
, and - a coverage interval containing
 with a specified coverage probability.
with a specified coverage probability.
The propagation stage of uncertainty evaluation is known as the propagation of distributions, various approaches for which are available, including
- the GUM uncertainty framework, constituting the application of the law of propagation of uncertainty, and the characterization of the output quantity
 by a Gaussian or a
by a Gaussian or a  -distribution,
-distribution, - analytic methods, in which mathematical analysis is used to derive an algebraic form for the probability distribution for
 , and
, and - a Monte Carlo methodMonte Carlo methodMonte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
, in which an approximation to the distribution function for is established numerically by making random draws from the probability distributions for the input quantities, and evaluating the model at the resulting values.
is established numerically by making random draws from the probability distributions for the input quantities, and evaluating the model at the resulting values.
For any particular uncertainty evaluation problem, approach 1), 2) or 3) (or some other approach) is used, 1) being generally approximate, 2) exact, and 3) providing a solution with a numerical accuracy that can be controlled.
Joint Committee for Guides in Metrology
In 1997 a Joint Committee for Guides in Metrology (JCGM), chaired by the Director of the BIPMInternational Bureau of Weights and Measures
The International Bureau of Weights and Measures , is an international standards organisation, one of three such organisations established to maintain the International System of Units under the terms of the Metre Convention...
, was created
by the seven international organizations that had originally in 1993 prepared the "Guide to the expression of uncertainty in measurement" (GUM) and the "International vocabulary of metrology – basic and general concepts and associated terms" (VIM). The JCGM assumed responsibility for these two documents from the ISO Technical
Advisory Group 4 (TAG4).
The Joint Committee is formed by the BIPM with the International Electrotechnical Commission (IEC), the International Federation of Clinical Chemistry and Laboratory Medicine (IFCC), the International Laboratory Accreditation Cooperation (ILAC), the International Organization for Standardization (ISO), the International Union of Pure and Applied Chemistry (IUPAC), the International Union of Pure and Applied Physics (IUPAP), and the International Organization of Legal Metrology (OIML).
JCGM has two Working Groups. Working Group 1, "Expression of uncertainty in measurement", has the task to promote the use of the GUM and to prepare Supplements and other documents for its broad application. Working Group 2, "Working Group on International vocabulary of basic and general terms in metrology (VIM)", has the task to revise and promote the use of the VIM. For further information on the activity of the JCGM, see www.bipm.org.
Revision by Working Group 1 of the GUM itself has started in parallel with work on preparing documents in a series of JCGM documents under the generic heading Evaluation of
measurement data. The parts in the series are
- JCGM 100:2008. Evaluation of measurement data — Guide to the expression of uncertainty in measurement (GUM),
- JCGM 101:2008. Evaluation of measurement data – Supplement 1 to the "Guide to the expression of uncertainty in measurement" – Propagation of distributions using a Monte Carlo method,
- JCGM 102. Evaluation of measurement data – Supplement 2 to the "Guide to the expression of uncertainty in measurement" – Models with any number of output quantities,
- JCGM 103. Evaluation of measurement data – Supplement 3 to the "Guide to the expression of uncertainty in measurement" – Modelling,
- JCGM 104:2000. Evaluation of measurement data – An introduction to the "Guide to the expression of uncertainty in measurement" and related documents,
- JCGM 105. Evaluation of measurement data – Concepts and basic principles,
- JCGM 106. Evaluation of measurement data – The role of measurement uncertainty in conformity assessment, and
- JCGM 107. Evaluation of measurement data – Applications of the least-squares method.
Alternative Perspective
Most of this article represents the most common view of measurement uncertainty, which assumesthat random variables are proper mathematical models for uncertain quantities and simple
probability distributions are sufficient for representing all forms of measurement uncertainties.
In some situations, however, a mathematical interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
rather than a probability
distribution might be a better model of uncertainty. This may include situations involving periodic measurements,
binned
Data binning
Data binning is a data pre-processing technique used to reduce the effects of minor observation errors. The original data values which fall in a given small interval, a bin, are replaced by a value representative of that interval, often the central value...
data values, censoring
Censoring (statistics)
In statistics, engineering, and medical research, censoring occurs when the value of a measurement or observation is only partially known.For example, suppose a study is conducted to measure the impact of a drug on mortality. In such a study, it may be known that an individual's age at death is at...
, detection limits, or
plus-minus ranges of measurements where no particular probability distribution seems justified or
where one cannot assume that the errors among individual measuresments are completely independent.
A more robust
Robust statistics
Robust statistics provides an alternative approach to classical statistical methods. The motivation is to produce estimators that are not unduly affected by small departures from model assumptions.- Introduction :...
representation of measurement uncertainty in such cases can be fashioned from intervals.
An interval [a,b] is different from a rectangular or uniform probability distribution over the same range in that the
latter suggests that the true value lies inside the right half of the range [(a+b)/2, b] with
probability one half, and within any subinterval of [a,b] with probability equal to the width of the subinterval divided by b–a.
The interval makes no such claims, except simply that the measurement lies somewhere within the interval.
Distributions of such measurement intervals can be summarized as
probability box
Probability box
A probability box is a characterization of an uncertain number consisting of both aleatoric and epistemic uncertainties that is often used in risk analysis or quantitative uncertainty modeling where numerical calculations must be performed...
es and Dempster-Shafer structures
Dempster-Shafer theory
The Dempster–Shafer theory is a mathematical theory of evidence. It allows one to combine evidence from different sources and arrive at a degree of belief that takes into account all the available evidence. The theory was first developed by Arthur P...
over the real
numbers, which incorporate both aleatoric and epistemic uncertainties
Uncertainty quantification
Uncertainty quantification is the science of quantitative characterization and reduction of uncertainties in applications. It tries to determine how likely certain outcomes are if some aspects of the system are not exactly known...
.
See also
- MetrologyMetrologyMetrology is the science of measurement. Metrology includes all theoretical and practical aspects of measurement. The word comes from Greek μέτρον , "measure" + "λόγος" , amongst others meaning "speech, oration, discourse, quote, study, calculation, reason"...
- Experimental uncertainty analysisExperimental uncertainty analysisThe purpose of this introductory article is to discuss the experimental uncertainty analysis of a derived quantity, based on the uncertainties in the experimentally measured quantities that are used in some form of mathematical relationship to calculate that derived quantity...
- Test methodTest methodA test method is a definitive procedure that produces a test result.A test can be considered as technical operation that consists of determination of one or more characteristics of a given product, process or service according to a specified procedure. Often a test is part of an experiment.The test...
- UncertaintyUncertaintyUncertainty is a term used in subtly different ways in a number of fields, including physics, philosophy, statistics, economics, finance, insurance, psychology, sociology, engineering, and information science...
- Confidence intervalConfidence intervalIn statistics, a confidence interval is a particular kind of interval estimate of a population parameter and is used to indicate the reliability of an estimate. It is an observed interval , in principle different from sample to sample, that frequently includes the parameter of interest, if the...
- Propagation of uncertaintyPropagation of uncertaintyIn statistics, propagation of error is the effect of variables' uncertainties on the uncertainty of a function based on them...
- List of uncertainty propagation software
Further reading
- JCGM 200:2008. International Vocabulary of Metrology - Basic and general concepts and associated terms, 3rd Edition. Joint Committee for Guides in Metrology.
- ISO 3534-1:2006. Statistics - Vocabulary and symbols - Part 1: General statistical terms and terms used in probability.
- Bell, S. Measurement Good Practice Guide No. 11. A Beginner's Guide to Uncertainty of Measurement.Technical report, National Physical Laboratory, 1999.
- Cox, M. G., and Harris, P. M. SSfM Best Practice Guide No. 6, Uncertainty evaluation. Technical report DEM-ES-011, National Physical Laboratory, 2006.
- Cox, M. G., and Harris, P. M. Software specifications for uncertainty evaluation. Technical report DEM-ES-010, National Physical Laboratory, 2006.
- http://www.springer.com/physics/book/978-3-540-20944-7 Grabe, M., Measurement Uncertainties in Science and Technology, Springer 2005
- http://www.springer.com/physics/book/978-3-642-03304-9 Grabe, M. Generalized Gaussian Error Calculus, Springer 2010
- Dietrich, C. F. Uncertainty, Calibration and Probability. Adam Hilger, Bristol, UK, 1991.
- NIST. Uncertainty of measurement results.
- Bich, W., Cox, M. G., and Harris, P. M. Evolution of the "Guide to the Expression of Uncertainty in Measurement". Metrologia, 43(4):S161–S166, 2006.
- EA. Expression of the uncertainty of measurement in calibration. Technical Report EA-4/02, European Co-operation for Accreditation, 1999.
- Elster, C., and Toman, B. Bayesian uncertainty analysis under prior ignorance of the measurand versus analysis using Supplement 1 to the Guide: a comparison. Metrologia, 46:261-266, 2009.
- Ferson, S., Kreinovich, V., Hajagos, J., Oberkampf, W., and Ginzburg, L. 2007. "Experimental Uncertainty Estimation and Statistics for Data Having Interval Uncertainty". SAND2007-0939.
- Lira., I. Evaluating the Uncertainty of Measurement. Fundamentals and Practical Guidance. Institute of Physics, Bristol, UK, 2002.
- Majcen N., Taylor P. (Editors), Practical examples on traceability, measurement uncertainty and validation in chemistry, Vol 1, 2010; ISBN 978-92-79-12021-3.
- UKAS. The expression of uncertainty in EMC testing. Technical Report LAB34, United Kingdom Accreditation Service, 2002.
- NPLUnc
- Estimate of temperature and its uncertainty in small systems, 2011. http://www.physik.uni-augsburg.de/theo1/hanggi/AJP.pdf

