Iteratively re-weighted least squares
Encyclopedia
The method of iteratively reweighted least squares (IRLS) is used to solve certain optimization problems. It solves objective functions of the form:
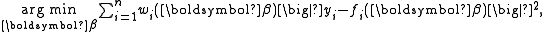
by an iterative method
in which each step involves solving a weighted least squares problem of the form:
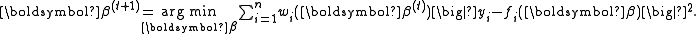
IRLS is used to find the maximum likelihood
estimates of a generalized linear model
, and in robust regression
to find an M-estimator
, as a way of mitigating the influence of outliers in an otherwise normally-distributed data set. For example, by minimizing the least absolute error rather than the least square error.
Although not a linear regression problem, Weiszfeld's algorithm for approximating the geometric median
can also be viewed as a special case of iteratively reweighted least squares, in which the objective function is the sum of distances of the estimator from the samples.
One of the advantages of IRLS over linear
and convex programming is that it can be used with Gauss–Newton and Levenberg–Marquardt numerical algorithms.
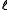1 minimization and smoothed 
p minimization, p<1, in the compressed sensing
problems. It has been proved that the algorithm has a linear rate of convergence for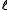
1 norm and superlinear for 
t with t < 1, under the restricted isometry property
, which is generally a sufficient condition for sparse solutions.
for the linear regression
problem,
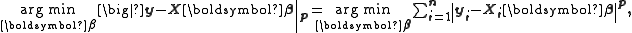
the IRLS algorithm at step t+1 involves solving the weighted linear least squares problem:
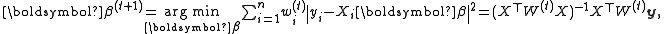
where W(t) is the diagonal matrix
of weights with elements:
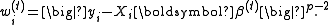
In the case p = 1, this corresponds to least absolute deviation regression (in this case, the problem would be better approached by use of linear programming
methods).
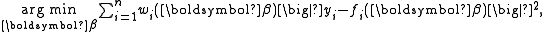
by an iterative method
Iterative method
In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...
in which each step involves solving a weighted least squares problem of the form:
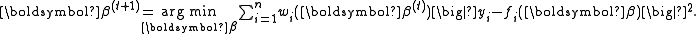
IRLS is used to find the maximum likelihood
Maximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
estimates of a generalized linear model
Generalized linear model
In statistics, the generalized linear model is a flexible generalization of ordinary linear regression. The GLM generalizes linear regression by allowing the linear model to be related to the response variable via a link function and by allowing the magnitude of the variance of each measurement to...
, and in robust regression
Robust regression
In robust statistics, robust regression is a form of regression analysis designed to circumvent some limitations of traditional parametric and non-parametric methods. Regression analysis seeks to find the effect of one or more independent variables upon a dependent variable...
to find an M-estimator
M-estimator
In statistics, M-estimators are a broad class of estimators, which are obtained as the minima of sums of functions of the data. Least-squares estimators and many maximum-likelihood estimators are M-estimators. The definition of M-estimators was motivated by robust statistics, which contributed new...
, as a way of mitigating the influence of outliers in an otherwise normally-distributed data set. For example, by minimizing the least absolute error rather than the least square error.
Although not a linear regression problem, Weiszfeld's algorithm for approximating the geometric median
Geometric median
The geometric median of a discrete set of sample points in a Euclidean space is the point minimizing the sum of distances to the sample points. This generalizes the median, which has the property of minimizing the sum of distances for one-dimensional data, and provides a central tendency in higher...
can also be viewed as a special case of iteratively reweighted least squares, in which the objective function is the sum of distances of the estimator from the samples.
One of the advantages of IRLS over linear
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
and convex programming is that it can be used with Gauss–Newton and Levenberg–Marquardt numerical algorithms.
L1 minimization for sparse recovery
IRLS can be used for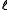1 minimization and smoothed p minimization, p<1, in the compressed sensingCompressed sensing
Compressed sensing, also known as compressive sensing, compressive sampling and sparse sampling, is a technique for finding sparse solutions to underdetermined linear systems...
problems. It has been proved that the algorithm has a linear rate of convergence for
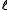1 norm and superlinear for t with t < 1, under the restricted isometry propertyRestricted isometry property
In linear algebra, the restricted isometry property characterizes matrices which are nearly orthonormal, at least when operating on sparse vectors. The concept was introduced by Emmanuel Candès and Terence Tao and is used to prove many theorems in the field of compressed sensing...
, which is generally a sufficient condition for sparse solutions.
Lp norm linear regression
To find the parameters β = (β1, …,βk)T which minimize the Lp normLp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
for the linear regression
Linear regression
In statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression...
problem,
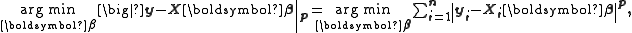
the IRLS algorithm at step t+1 involves solving the weighted linear least squares problem:
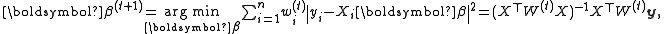
where W(t) is the diagonal matrix
Diagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
of weights with elements:
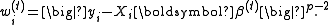
In the case p = 1, this corresponds to least absolute deviation regression (in this case, the problem would be better approached by use of linear programming
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
methods).