
Geometric median
Encyclopedia
The geometric median of a discrete set of sample points in a Euclidean space
is the point minimizing the sum of distances to the sample points. This generalizes the median
, which has the property of minimizing the sum of distances for one-dimensional data, and provides a central tendency
in higher dimensions. It is also known as the Fermat–Weber point or 1-median.
The geometric median is an important estimator
of location
in statistics. It is also a standard problem in facility location
, where it models the problem of locating a facility to minimize the cost of transportation.
The special case of the problem for three points in the plane (that is, m = 3 and n = 2) is sometimes also known as Fermat's problem; it arises in the construction of minimal Steiner tree
s, and was originally posed as a problem by Pierre de Fermat
to Evangelista Torricelli
, who solved it. Its solution is now known as the Fermat point
of the triangle formed by the three sample points. Alfred Weber
's name is associated with the more general Fermat–Weber problem due to a discussion of the problem in his 1909 book on facility location.
Wesolowsky (1993) provides a survey of the problem. See Fekete, Mitchell, and Beurer (2003) for generalizations of the problem to non-discrete point sets.
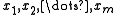 with each
with each 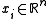 , the geometric median is defined as
, the geometric median is defined as
Note that argmin means the value of the argument which minimizes the sum. In this case, it is the point
which minimizes the sum. In this case, it is the point 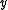 from where the sum of all Euclidean distance
from where the sum of all Euclidean distance
s to the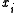 's is minimum.
's is minimum.
or center of mass
, defined similarly to the geometric median as minimizing the sum of the squares of the distances to each sample, can be found by a simple formula — its coordinates are the averages of the coordinates of the samples — but no such formula is known for the geometric median, and it has been shown that no explicit formula, nor an exact algorithm involving only arithmetic operations and kth roots can exist in general. Therefore only numerical or symbolic approximations to the solution of this problem are possible under this model of computation
.
However, it is straightforward to calculate an approximation to the geometric median using an iterative procedure in which each step produces a more accurate approximation. Procedures of this type can be derived from the fact that the sum of distances is a convex function
, since the distance to each sample point is convex and the sum of convex functions remains convex. Therefore, procedures that decrease the sum of distances at each step cannot get trapped in a local optimum
.
One common approach of this type, called Weiszfeld's algorithm, is a form of iteratively re-weighted least squares
. This algorithm defines a set of weights that are inversely proportional to the distances from the current estimate to the samples, and creates a new estimate that is the weighted average of the samples according to these weights. That is,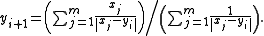
Bose et al. (2003) describe more sophisticated geometric optimization procedures for finding approximately optimal solutions to this problem. As show, the problem can also be represented as a semidefinite program
.
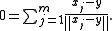
This is equivalent to: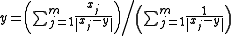
which is closely related to Weiszfeld's algorithm.
If y is equal to some of the given points, then y is the geometric median if and only if there are vectors uj such that: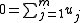
where for xj ≠ y,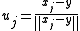
and for xj = y,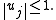
s (and even metric space
s) using the same idea which is used to define the Fréchet mean
on a Riemannian manifold. Let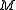 be a Riemannian manifold with corresponding distance function
be a Riemannian manifold with corresponding distance function 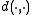 , let
, let 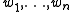 be
be  weights summing to 1, and let
weights summing to 1, and let 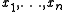
be observations from
observations from 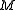 . Then we define the weighted geometric median
. Then we define the weighted geometric median 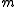 (or weighted Fréchet median) of the data points as
(or weighted Fréchet median) of the data points as
If all the weights are equal, we say simply that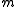 is the geometric median.
is the geometric median.
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
is the point minimizing the sum of distances to the sample points. This generalizes the median
Median
In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
, which has the property of minimizing the sum of distances for one-dimensional data, and provides a central tendency
Central tendency
In statistics, the term central tendency relates to the way in which quantitative data is clustered around some value. A measure of central tendency is a way of specifying - central value...
in higher dimensions. It is also known as the Fermat–Weber point or 1-median.
The geometric median is an important estimator
Estimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
of location
Location parameter
In statistics, a location family is a class of probability distributions that is parametrized by a scalar- or vector-valued parameter μ, which determines the "location" or shift of the distribution...
in statistics. It is also a standard problem in facility location
Facility location
Facility location, also known as location analysis, is a branch of operations research and computational geometry concerning itself with mathematical modeling and solution of problems concerning optimal placement of facilities in order to minimize transportation costs, avoid placing hazardous...
, where it models the problem of locating a facility to minimize the cost of transportation.
The special case of the problem for three points in the plane (that is, m = 3 and n = 2) is sometimes also known as Fermat's problem; it arises in the construction of minimal Steiner tree
Steiner tree
The Steiner tree problem, or the minimum Steiner tree problem, named after Jakob Steiner, is a problem in combinatorial optimization, which may be formulated in a number of settings, with the common part being that it is required to find the shortest interconnect for a given set of objects.The...
s, and was originally posed as a problem by Pierre de Fermat
Pierre de Fermat
Pierre de Fermat was a French lawyer at the Parlement of Toulouse, France, and an amateur mathematician who is given credit for early developments that led to infinitesimal calculus, including his adequality...
to Evangelista Torricelli
Evangelista Torricelli
Evangelista Torricelli was an Italian physicist and mathematician, best known for his invention of the barometer.-Biography:Evangelista Torricelli was born in Faenza, part of the Papal States...
, who solved it. Its solution is now known as the Fermat point
Fermat point
In geometry the Fermat point of a triangle, also called Torricelli point, is a point such that the total distance from the three vertices of the triangle to the point is the minimum possible...
of the triangle formed by the three sample points. Alfred Weber
Alfred Weber
Alfred Weber was a German economist, sociologist and theoretician of culture whose work was influential in the development of modern economic geography.-Life:...
's name is associated with the more general Fermat–Weber problem due to a discussion of the problem in his 1909 book on facility location.
Wesolowsky (1993) provides a survey of the problem. See Fekete, Mitchell, and Beurer (2003) for generalizations of the problem to non-discrete point sets.
Definition
Formally, for a given set of m points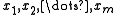 with each
with each 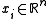 , the geometric median is defined as
, the geometric median is defined as- Geometric Median
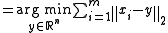
Note that argmin means the value of the argument
 which minimizes the sum. In this case, it is the point
which minimizes the sum. In this case, it is the point 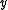 from where the sum of all Euclidean distance
from where the sum of all Euclidean distanceEuclidean distance
In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
s to the
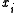 's is minimum.
's is minimum.Properties
- For the 1-dimensional case, the geometric median coincides with the medianMedianIn probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
. This is because the univariateUnivariateIn mathematics, univariate refers to an expression, equation, function or polynomial of only one variable. Objects of any of these types but involving more than one variable may be called multivariate...
median also minimizes the sum of distances from the points. - The geometric median is unique whenever the points are not collinearLine (geometry)The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
. - The geometric median is equivariantEquivariantIn mathematics, an equivariant map is a function between two sets that commutes with the action of a group. Specifically, let G be a group and let X and Y be two associated G-sets. A function f : X → Y is said to be equivariant iffor all g ∈ G and all x in X...
for Euclidean similarity transformationsSimilarity (geometry)Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
, including translationTranslation (geometry)In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
and rotationRotation (mathematics)In geometry and linear algebra, a rotation is a transformation in a plane or in space that describes the motion of a rigid body around a fixed point. A rotation is different from a translation, which has no fixed points, and from a reflection, which "flips" the bodies it is transforming...
. This means that one would get the same result either by transforming the geometric median, or by applying the same transformation to the sample data and finding the geometric median of the transformed data. This property follows from the fact that the geometric median is defined only from pairwise distances, and doesn't depend on the system of orthogonal Cartesian coordinates by which the sample data is represented. In contrast, the component-wise median for a multivariate data set is not in general rotation invariant, nor is it independent of the choice of coordinates. - The geometric median has a breakdown point of 0.5. That is, up to half of the sample data may be arbitrarily corrupted, and the median of the samples will still provide a robust estimator for the location of the uncorrupted data.
Special cases
- For 3 points, if any angle of the triangle is more than 120° then the geometric median is the point making that angle. If all the angles are less than 120°, the geometric median is the point inside the triangle which subtends an angle of 120° to all three pairs of points. This is also known as the Fermat pointFermat pointIn geometry the Fermat point of a triangle, also called Torricelli point, is a point such that the total distance from the three vertices of the triangle to the point is the minimum possible...
of the triangle formed by the three points. - For 4 coplanar points, if one of the four points is inside the triangle formed by the other three points, then the geometric median is that point. Otherwise, the points form a convex quadrilateralQuadrilateralIn Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...
and the geometric median is the crossing point of the diagonals of the quadrilateral. The geometric median of four coplanar points is the same as the unique Radon point of the four points.
Computation
Despite being an easy to understand concept, computing the geometric median poses a challenge. The centroidCentroid
In geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...
or center of mass
Center of mass
In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...
, defined similarly to the geometric median as minimizing the sum of the squares of the distances to each sample, can be found by a simple formula — its coordinates are the averages of the coordinates of the samples — but no such formula is known for the geometric median, and it has been shown that no explicit formula, nor an exact algorithm involving only arithmetic operations and kth roots can exist in general. Therefore only numerical or symbolic approximations to the solution of this problem are possible under this model of computation
Model of computation
In computability theory and computational complexity theory, a model of computation is the definition of the set of allowable operations used in computation and their respective costs...
.
However, it is straightforward to calculate an approximation to the geometric median using an iterative procedure in which each step produces a more accurate approximation. Procedures of this type can be derived from the fact that the sum of distances is a convex function
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
, since the distance to each sample point is convex and the sum of convex functions remains convex. Therefore, procedures that decrease the sum of distances at each step cannot get trapped in a local optimum
Local optimum
Local optimum is a term in applied mathematics and computer science.A local optimum of a combinatorial optimization problem is a solution that is optimal within a neighboring set of solutions...
.
One common approach of this type, called Weiszfeld's algorithm, is a form of iteratively re-weighted least squares
Iteratively re-weighted least squares
The method of iteratively reweighted least squares is used to solve certain optimization problems. It solves objective functions of the form:...
. This algorithm defines a set of weights that are inversely proportional to the distances from the current estimate to the samples, and creates a new estimate that is the weighted average of the samples according to these weights. That is,
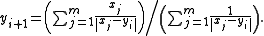
Bose et al. (2003) describe more sophisticated geometric optimization procedures for finding approximately optimal solutions to this problem. As show, the problem can also be represented as a semidefinite program
Semidefinite programming
Semidefinite programming is a subfield of convex optimization concerned with the optimization of a linear objective functionover the intersection of the cone of positive semidefinite matrices with an affine space, i.e., a spectrahedron....
.
Implicit formula
If y is distinct from all the given points, xj, then y is the geometric median if and only if it satisfies: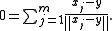
This is equivalent to:
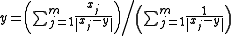
which is closely related to Weiszfeld's algorithm.
If y is equal to some of the given points, then y is the geometric median if and only if there are vectors uj such that:
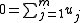
where for xj ≠ y,
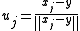
and for xj = y,
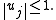
Generalizations
The geometric median can be generalized from Euclidean spaces to general Riemannian manifoldRiemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
s (and even metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s) using the same idea which is used to define the Fréchet mean
Fréchet mean
The Fréchet mean , is the point, x, that minimizes the Fréchet function, in cases where such a unique minimizer exists. The value at a point p, of the Fréchet function associated to a random point X on a complete metric space is the expected squared distance from p to X...
on a Riemannian manifold. Let
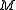 be a Riemannian manifold with corresponding distance function
be a Riemannian manifold with corresponding distance function 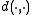 , let
, let 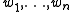 be
be  weights summing to 1, and let
weights summing to 1, and let 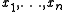
be
 observations from
observations from 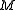 . Then we define the weighted geometric median
. Then we define the weighted geometric median 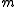 (or weighted Fréchet median) of the data points as
(or weighted Fréchet median) of the data points as
-
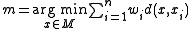 .
.
If all the weights are equal, we say simply that
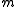 is the geometric median.
is the geometric median.See also
- Central tendencyCentral tendencyIn statistics, the term central tendency relates to the way in which quantitative data is clustered around some value. A measure of central tendency is a way of specifying - central value...
- CentroidCentroidIn geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...
, which minimizes the sum of squares of Euclidean distance - meanMeanIn statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
- Fréchet meanFréchet meanThe Fréchet mean , is the point, x, that minimizes the Fréchet function, in cases where such a unique minimizer exists. The value at a point p, of the Fréchet function associated to a random point X on a complete metric space is the expected squared distance from p to X...

