In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, the Euler line, named after Leonhard Euler

Leonhard Euler

Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...

, is a line

Line (mathematics)

The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...

 determined from any triangle

Triangle

A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....

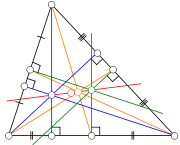
 that is not equilateral; it passes through several important points determined from the triangle. It passes through the orthocenter, the circumcenter, the centroid

Centroid

In geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...

, and the center of the nine-point circle

Nine-point circle

In geometry, the nine-point circle is a circle that can be constructed for any given triangle. It is so named because it passes through nine significant points defined from the triangle...

 of the triangle.

Euler showed in 1765 that in any triangle, the orthocenter, circumcenter and centroid are collinear

Line (geometry)

The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...

. This property is also true for the nine-point center, although it had not been defined in Euler's time. In equilateral triangles, these four points coincide, but in any other triangle they do not, and the Euler line is determined by any two of them. The center of the nine-point circle lies midway along the Euler line between the orthocenter and the circumcenter, and the distance from the centroid to the circumcenter is half that from the centroid to the orthocenter.

Other notable points that lie on the Euler line are the de Longchamps point

De Longchamps point

In geometry, the de Longchamps point of a triangle is the reflection of its orthocenter about its circumcenter. It is listed as X in the Encyclopedia of Triangle Centers. Its trilinear coordinates are\displaystyle\cos A - \cos B \cos C : \cos B - \cos C \cos A : \cos C - \cos A \cos BThe point is...

, the Schiffler point

Schiffler point

In geometry, the Schiffler point of a triangle is a point defined from the triangle that is invariant under Euclidean transformations of the triangle. This point was first defined and investigated by Schiffler et al...

, the Exeter point and the far-out point. However, the incenter lies on the Euler line only for isosceles triangles.

The Euler line is its own complement, and therefore also its own anticomplement.

Let A, B, C denote the vertex angles of the reference triangle, and let x : y : z be a variable point in trilinear coordinates

Trilinear coordinates

In geometry, the trilinear coordinates of a point relative to a given triangle describe the relative distances from the three sides of the triangle. Trilinear coordinates are an example of homogeneous coordinates...

; then an equation for the Euler line is


Another particularly useful way to represent the Euler line is in terms of a parameter t. Starting with the circumcenter (with trilinears ) and the orthocenter (with trilinears , every point on the Euler line, except the orthocenter, is given as


for some t.

Examples:

• centroid
  Centroid
  In geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...
  
   =
• nine-point center =
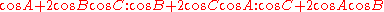
• De Longchamps point
  De Longchamps point
  In geometry, the de Longchamps point of a triangle is the reflection of its orthocenter about its circumcenter. It is listed as X in the Encyclopedia of Triangle Centers. Its trilinear coordinates are\displaystyle\cos A - \cos B \cos C : \cos B - \cos C \cos A : \cos C - \cos A \cos BThe point is...
  
   =
• Euler infinity point =

External links

• Altitudes and the Euler Line and Euler Line and 9-Point Circle at cut-the-knot
  Cut-the-knot
  Cut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
  
  
• Triangle centers on the Euler line, by Clark Kimberling.
• An interactive applet showing several triangle centers that lies on the Euler line.
• "Euler Line" by Eric Rowland, the Wolfram Demonstrations Project
  Wolfram Demonstrations Project
  The Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
  
  , 2007.
• Nine-point conic and Euler line generalization at Dynamic Geometry Sketches Generalizes nine-point circle to a nine-point conic with an associated generalization of the Euler line.