Exceptional divisor
Encyclopedia
In mathematics
, specifically algebraic geometry
, an exceptional divisor for a regular map
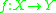
of varieties is a kind of 'large' subvariety of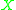
which is 'crushed' by 
, in a certain definite sense. More strictly, f has an associated exceptional locus which describes how it identifies nearby points in codimension one, and the exceptional divisor is an appropriate algebraic construction whose support is the exceptional locus. The same ideas can be found in the theory of holomorphic mappings of complex manifold
s.
More precisely, suppose that
is a regular map of varieties which is birational (that is, it is an isomorphism between open subsets of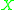
and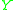 
). A codimension-1 subvariety 
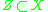is said to be exceptional if 
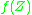has codimension at least 2 as a subvariety of 
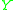. One may then define the exceptional divisor of 
to be
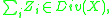
where the sum is over all exceptional subvarieties of
, and is an element of the group of Weil divisors
on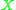
.
Consideration of exceptional divisors is crucial in birational geometry
: an elementary result (see for instance Shafarevich, II.4.4) shows that any birational regular map that is not an isomorphism has an exceptional divisor. A particularly important example is the blowup
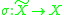
of a subvariety
:
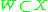in this case the exceptional divisor is exactly the preimage of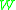
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, an exceptional divisor for a regular map
Regular map (algebraic geometry)
In algebraic geometry, a regular map between affine varieties is a mapping which is given by polynomials. For example, if X and Y are subvarieties of An resp...
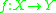
of varieties is a kind of 'large' subvariety of
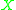which is 'crushed' by , in a certain definite sense. More strictly, f has an associated exceptional locus which describes how it identifies nearby points in codimension one, and the exceptional divisor is an appropriate algebraic construction whose support is the exceptional locus. The same ideas can be found in the theory of holomorphic mappings of complex manifoldComplex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
s.
More precisely, suppose that
is a regular map of varieties which is birational (that is, it is an isomorphism between open subsets of
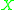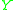and ). A codimension-1 subvariety 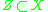is said to be exceptional if 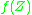has codimension at least 2 as a subvariety of 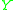. One may then define the exceptional divisor of to be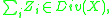where the sum is over all exceptional subvarieties of
, and is an element of the group of Weil divisorsDivisor (algebraic geometry)
In algebraic geometry, divisors are a generalization of codimension one subvarieties of algebraic varieties; two different generalizations are in common use, Cartier divisors and Weil divisors...
on
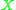.Consideration of exceptional divisors is crucial in birational geometry
Birational geometry
In mathematics, birational geometry is a part of the subject of algebraic geometry, that deals with the geometry of an algebraic variety that is dependent only on its function field. In the case of dimension two, the birational geometry of algebraic surfaces was largely worked out by the Italian...
: an elementary result (see for instance Shafarevich, II.4.4) shows that any birational regular map that is not an isomorphism has an exceptional divisor. A particularly important example is the blowup
Blowing up
In mathematics, blowing up or blowup is a type of geometric transformation which replaces a subspace of a given space with all the directions pointing out of that subspace. For example, the blowup of a point in a plane replaces the point with the projectivized tangent space at that point...
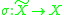
of a subvariety
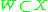:in this case the exceptional divisor is exactly the preimage of
.
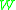