Exergy efficiency
Encyclopedia
Exergy efficiency computes the efficiency of a process taking the second law of thermodynamics into account.
it can be demonstrated that no system can ever be 100% efficient. When calculating the energy efficiency of a system, the figure found gives no indication of how the system compares to a thermodynamically perfect one operating under the same conditions. In comparison, the rational efficiency of a system can reach 100% because the work output is compared to the potential of the input to do work. The energy efficiencies of a heat engine are always smaller than its exergy efficiency.
B balance of a process gives:
with exergy efficiency defined as:
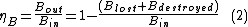
For many engineering systems this can be rephrased as:
Where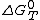
is the standard free enthalpy
of reaction at temperature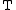
and pressure 
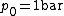(also known as the standard Gibbs function change), 
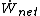is the net work output and 
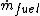is the mass flow rate of fuel.
In the same way the energy efficiency can be defined as:
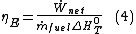
Where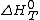
is the standard enthalpy of reaction at temperature 
and pressure 
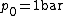, for all fuels 
so the exergy efficiency must always be greater than the energy efficiency.
For fossil fuels the free enthalpy of reaction is usually only slightly less than the enthalpy of reaction so from equations (3) and (4) we can see that the energy efficiency will be correspondingly larger than the energy law efficiency. For example, a typical combined cycle power plant burning methane may have an energy efficiency of 55%, while its exergy efficiency will be 57%. A 100% exergy efficient methane fired power station would correspond to an energy efficiency of 98%.
This means that for many of the fuels we use, the maximum efficiency that can be achieved is >90%, however we are restricted to the Carnot efficiency in many situations as a heat engine is being used.
. This is incorrect because a Carnot engine is the most efficient heat engine possible, but not the most efficient device for creating work. Fuel cells, for instance, can theoretically reach much higher efficiencies than a Carnot engine.
(Gilliland 1978, p. 101).
Motivation
From the second law of thermodynamicsSecond law of thermodynamics
The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
it can be demonstrated that no system can ever be 100% efficient. When calculating the energy efficiency of a system, the figure found gives no indication of how the system compares to a thermodynamically perfect one operating under the same conditions. In comparison, the rational efficiency of a system can reach 100% because the work output is compared to the potential of the input to do work. The energy efficiencies of a heat engine are always smaller than its exergy efficiency.
Definition
The energyEnergy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
B balance of a process gives:
with exergy efficiency defined as:
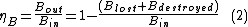
For many engineering systems this can be rephrased as:
Where
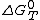is the standard free enthalpyEnthalpy
Enthalpy is a measure of the total energy of a thermodynamic system. It includes the internal energy, which is the energy required to create a system, and the amount of energy required to make room for it by displacing its environment and establishing its volume and pressure.Enthalpy is a...
of reaction at temperature
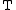and pressure 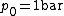(also known as the standard Gibbs function change), 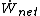is the net work output and 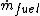is the mass flow rate of fuel.In the same way the energy efficiency can be defined as:
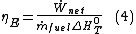
Where
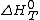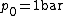is the standard enthalpy of reaction at temperature and pressure , for all fuels so the exergy efficiency must always be greater than the energy efficiency.Application
The destruction of exergy is closely related to the creation of entropy and as such any system containing highly irreversible processes will have a low energy efficiency. As an example the combustion process inside a power stations gas turbine is highly irreversible and approximately 25% of the exergy input will be destroyed here.For fossil fuels the free enthalpy of reaction is usually only slightly less than the enthalpy of reaction so from equations (3) and (4) we can see that the energy efficiency will be correspondingly larger than the energy law efficiency. For example, a typical combined cycle power plant burning methane may have an energy efficiency of 55%, while its exergy efficiency will be 57%. A 100% exergy efficient methane fired power station would correspond to an energy efficiency of 98%.
This means that for many of the fuels we use, the maximum efficiency that can be achieved is >90%, however we are restricted to the Carnot efficiency in many situations as a heat engine is being used.
Carnot
A common misconception is that the energy efficiency compares a given cycle to a Carnot heat engineCarnot heat engine
A Carnot heat engine is a hypothetical engine that operates on the reversible Carnot cycle. The basic model for this engine was developed by Nicolas Léonard Sadi Carnot in 1824...
. This is incorrect because a Carnot engine is the most efficient heat engine possible, but not the most efficient device for creating work. Fuel cells, for instance, can theoretically reach much higher efficiencies than a Carnot engine.
Second law efficiency under maximum power
Neither first or second laws of thermodynamics include a measure of the rate of energy transformation. When a measure of the maximal rate of energy transformation is included in the measure of second law efficiency it is known as second law efficiency under maximum power, and directly related to the maximum power principleMaximum power principle
The maximum power principle has been proposed as the fourth principle of energetics in open system thermodynamics, where an example of an open system is a biological cell. According to Howard T...
(Gilliland 1978, p. 101).