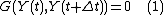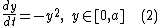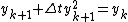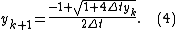Explicit and implicit methods
Encyclopedia
Explicit and implicit methods are approaches used in numerical analysis
for obtaining numerical solutions of time-dependent ordinary
and partial differential equation
s, as is required in computer simulation
s of physical processes
.
Explicit methods calculate the state of a system at a later time from the state of the system at the current time, while implicit methods find a solution by solving an equation involving both the current state of the system and the later one. Mathematically, if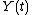
is the current system state and 
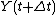is the state at the later time (
is a small time step), then, for an explicit method
while for an implicit method one solves an equation
to find
It is clear that implicit methods require an extra computation (solving the above equation), and they can be much harder to implement. Implicit methods are used because many problems arising in practice are stiff
, for which the use of an explicit method requires impractically small time steps
to keep the error in the result bounded (see numerical stability
). For such problems, to achieve given accuracy, it takes much less computational time to use an implicit method with larger time steps, even taking into account that one needs to solve an equation of the form (1) at each time step. That said, whether one should use an explicit or implicit method depends upon the problem to be solved.
with the initial condition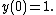
Consider a grid 
for 0≤k≤n, that is, the time step is 
and denote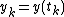 
for each 
. Discretize
this equation using the simplest explicit and implicit methods, which are the forward Euler and backward Euler methods (see numerical ordinary differential equations
) and compare the obtained schemes.
Forward Euler method:
The forward Euler method
yields
for each
This is an explicit formula for 
.
Backward Euler method:
With the backward Euler method
one finds the implicit equation
for
(compare this with formula (3) where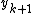 
was given explicitly rather than as an unknown in an equation).
This is a quadratic equation
, having one negative and one positive root. The positive root is picked because in the original equation the initial condition is positive, and then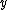
at the next time step is given by
In the vast majority of cases, the equation to be solved when using an implicit scheme is much more complicated than a quadratic equation, and no exact solution exists. Then one uses root-finding algorithm
s, such as Newton's method
.
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
for obtaining numerical solutions of time-dependent ordinary
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
and partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s, as is required in computer simulation
Computer simulation
A computer simulation, a computer model, or a computational model is a computer program, or network of computers, that attempts to simulate an abstract model of a particular system...
s of physical processes
Process (science)
In science, a process is every sequence of changes of a real object/body which is observable using the scientific method. Therefore, all sciences analyze and model processes....
.
Explicit methods calculate the state of a system at a later time from the state of the system at the current time, while implicit methods find a solution by solving an equation involving both the current state of the system and the later one. Mathematically, if
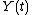is the current system state and 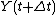is the state at the later time ( is a small time step), then, for an explicit method
while for an implicit method one solves an equation
to find
It is clear that implicit methods require an extra computation (solving the above equation), and they can be much harder to implement. Implicit methods are used because many problems arising in practice are stiff
Stiff equation
In mathematics, a stiff equation is a differential equation for which certain numerical methods for solving the equation are numerically unstable, unless the step size is taken to be extremely small. It has proved difficult to formulate a precise definition of stiffness, but the main idea is that...
, for which the use of an explicit method requires impractically small time steps
to keep the error in the result bounded (see numerical stabilityNumerical stability
In the mathematical subfield of numerical analysis, numerical stability is a desirable property of numerical algorithms. The precise definition of stability depends on the context, but it is related to the accuracy of the algorithm....
). For such problems, to achieve given accuracy, it takes much less computational time to use an implicit method with larger time steps, even taking into account that one needs to solve an equation of the form (1) at each time step. That said, whether one should use an explicit or implicit method depends upon the problem to be solved.
Illustration using the forward and backward Euler methods
Consider the ordinary differential equationOrdinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
with the initial condition
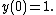Consider a grid for 0≤k≤n, that is, the time step is and denote 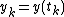for each . DiscretizeDiscretization
In mathematics, discretization concerns the process of transferring continuous models and equations into discrete counterparts. This process is usually carried out as a first step toward making them suitable for numerical evaluation and implementation on digital computers...
this equation using the simplest explicit and implicit methods, which are the forward Euler and backward Euler methods (see numerical ordinary differential equations
Numerical ordinary differential equations
Numerical ordinary differential equations is the part of numerical analysis which studies the numerical solution of ordinary differential equations...
) and compare the obtained schemes.
Forward Euler method:
The forward Euler method
yields
for each
This is an explicit formula for .Backward Euler method:
With the backward Euler method
one finds the implicit equation
for
(compare this with formula (3) where 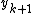was given explicitly rather than as an unknown in an equation).This is a quadratic equation
Quadratic equation
In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...
, having one negative and one positive root. The positive root is picked because in the original equation the initial condition is positive, and then
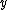at the next time step is given by
In the vast majority of cases, the equation to be solved when using an implicit scheme is much more complicated than a quadratic equation, and no exact solution exists. Then one uses root-finding algorithm
Root-finding algorithm
A root-finding algorithm is a numerical method, or algorithm, for finding a value x such that f = 0, for a given function f. Such an x is called a root of the function f....
s, such as Newton's method
Newton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
.