Exponential formula
Encyclopedia
In combinatorial
mathematics
, the exponential formula (called the polymer expansion in physics
) states that the exponential generating function for structures on finite sets is the exponential of the exponential generating function for connected structures.
The exponential formula is a power-series version of a special case of Faà di Bruno's formula
.
of the form
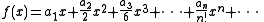
we have
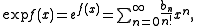
where
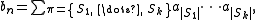
and the index π runs through the list of all partitions
{ S1, ..., Sk } of the set { 1, ..., n }. (When k = 0, the product is empty
and by definition equals 1.)
One can write the formula in the following form: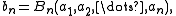
and thus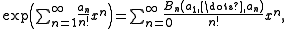
where Bn(a1, ..., an) is the nth complete Bell polynomial.
In quantum field theory and statistical mechanics, the partition function
s Z, or more generally correlation function
s, are give by a formal sum over Feynman diagram
s. The exponential formula shows that log(Z) can be given as a sum over connected Feynman diagrams, in terms of connected correlation functions.
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the exponential formula (called the polymer expansion in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
) states that the exponential generating function for structures on finite sets is the exponential of the exponential generating function for connected structures.
The exponential formula is a power-series version of a special case of Faà di Bruno's formula
Faà di Bruno's formula
Faà di Bruno's formula is an identity in mathematics generalizing the chain rule to higher derivatives, named after , though he was not the first to state or prove the formula...
.
Definition
For any formal power seriesFormal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
of the form
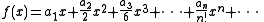
we have
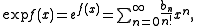
where
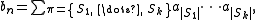
and the index π runs through the list of all partitions
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
{ S1, ..., Sk } of the set { 1, ..., n }. (When k = 0, the product is empty
Empty product
In mathematics, an empty product, or nullary product, is the result of multiplying no factors. It is equal to the multiplicative identity 1, given that it exists for the multiplication operation in question, just as the empty sum—the result of adding no numbers—is zero, or the additive...
and by definition equals 1.)
One can write the formula in the following form:
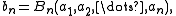
and thus
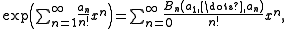
where Bn(a1, ..., an) is the nth complete Bell polynomial.
Examples
-
because there is one partition of the set { 1, 2, 3 } that has a single block of size 3, there are three partitions of { 1, 2, 3 } that split it into a block of size 2 and a block of size 1, and there is one partition of { 1, 2, 3 } that splits it into three blocks of size 1. - If bn = 2n(n−1)/2 is the number of graphs whose vertices are a given n-point set, then an is the number of connected graphs whose vertices are a given n-point set.
- There are numerous variations of the previous example where the graph has certain properties: for example, if bn counts graphs without cycles, then an counts trees (connected grphs without cycles).
- If bn counts directed graphs whose edges (rather than vertices) are a given n point set, then an counts connected directed graphs with this edge set.
Applications
In applications, the numbers an often count the number of some sort of "connected" structure on an n-point set, and the numbers bn count the number of (possibly disconnected) structures. The numbers bn/n! count the number of isomorphism classes of structures on n points, with each structure being weighted by the reciprocal of its automorphism group, and the numbers an/n! count isomorphism classes of connected structures in the same way.In quantum field theory and statistical mechanics, the partition function
Partition function (mathematics)
The partition function or configuration integral, as used in probability theory, information science and dynamical systems, is an abstraction of the definition of a partition function in statistical mechanics. It is a special case of a normalizing constant in probability theory, for the Boltzmann...
s Z, or more generally correlation function
Correlation function
A correlation function is the correlation between random variables at two different points in space or time, usually as a function of the spatial or temporal distance between the points...
s, are give by a formal sum over Feynman diagram
Feynman diagram
Feynman diagrams are a pictorial representation scheme for the mathematical expressions governing the behavior of subatomic particles, first developed by the Nobel Prize-winning American physicist Richard Feynman, and first introduced in 1948...
s. The exponential formula shows that log(Z) can be given as a sum over connected Feynman diagrams, in terms of connected correlation functions.