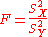F-test of equality of variances
Encyclopedia
In statistics, an F-test
for the null hypothesis
that two normal populations have the same variance
is sometimes used, although it needs to be used with caution as it can be sensitive to the assumption that the variables have this distribution.
Notionally, any F-test can be regarded as a comparison of two variances, but the specific case being discussed in this article is the two population one, where there are the test statistic
used in the ratio of two sample variances. This particular situation is of importance in mathematical statistics
since it provides a basic exemplar case in which the F-distribution can be derived. For application in applied statistics, there is concern that the test is so sensitive to the assumption of normality that it would be inadvisable to use it as a routine test for the equality of variances. In other words, this is a case where "approximate normality" (which in similar contexts would often be justified using the central limit theorem
), is not good enough to make the test procedure approximately valid to an acceptable degree.
s for the two populations can be different, and the hypothesis to be tested is that the variances are equal. Let
be the sample means. Let
be the sample variances. Then the test statistic
has an F-distribution with n − 1 and m − 1 degrees of freedom if the null hypothesis
of equality of variances is true. Otherwise it has a non-central F-distribution. The null hypothesis is rejected if F is either too large or too small.
, Bartlett's test
, or the Brown–Forsythe test are better tests for testing the equality of two variances. (However, all of these tests create experiment-wise Type I error inflations when conducted as a test of the assumption of homoscedasticity prior to a test of effects.) F-tests for the equality of variances can be used in practice, with care, particularly where a quick check is required, and subject to associated diagnostic checking: practical text-books suggest both graphical and formal checks of the assumption.
F-test
s are used for other statistical tests of hypotheses, such as testing for differences in means in three or more groups, or in factorial layouts. These F-tests are generally not robust
when there are violations of the assumption that each population follows the normal distribution, particularly for small alpha levels and unbalanced layouts. However, for large alpha levels (e.g., at least 0.05) and balanced layouts, the F-test is relatively robust, although (if the normality assumption does not hold) it suffers from a loss in comparative statistical power as compared with non-parametric counterparts.
and Bartlett's test
.
F-test
An F-test is any statistical test in which the test statistic has an F-distribution under the null hypothesis.It is most often used when comparing statistical models that have been fit to a data set, in order to identify the model that best fits the population from which the data were sampled. ...
for the null hypothesis
Null hypothesis
The practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
that two normal populations have the same variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
is sometimes used, although it needs to be used with caution as it can be sensitive to the assumption that the variables have this distribution.
Notionally, any F-test can be regarded as a comparison of two variances, but the specific case being discussed in this article is the two population one, where there are the test statistic
Test statistic
In statistical hypothesis testing, a hypothesis test is typically specified in terms of a test statistic, which is a function of the sample; it is considered as a numerical summary of a set of data that...
used in the ratio of two sample variances. This particular situation is of importance in mathematical statistics
Mathematical statistics
Mathematical statistics is the study of statistics from a mathematical standpoint, using probability theory as well as other branches of mathematics such as linear algebra and analysis...
since it provides a basic exemplar case in which the F-distribution can be derived. For application in applied statistics, there is concern that the test is so sensitive to the assumption of normality that it would be inadvisable to use it as a routine test for the equality of variances. In other words, this is a case where "approximate normality" (which in similar contexts would often be justified using the central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
), is not good enough to make the test procedure approximately valid to an acceptable degree.
The test
Let X1, ..., Xn and Y1, ..., Ym be independent and identically distributed samples from two populations which each have a normal distribution. The expected valueExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
s for the two populations can be different, and the hypothesis to be tested is that the variances are equal. Let
be the sample means. Let
be the sample variances. Then the test statistic
has an F-distribution with n − 1 and m − 1 degrees of freedom if the null hypothesis
Null hypothesis
The practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
of equality of variances is true. Otherwise it has a non-central F-distribution. The null hypothesis is rejected if F is either too large or too small.
Properties
This F-test is known to be extremely sensitive to non-normality, so Levene's testLevene's test
In statistics, Levene's test is an inferential statistic used to assess the equality of variances in different samples. Some common statistical procedures assume that variances of the populations from which different samples are drawn are equal. Levene's test assesses this assumption. It tests the...
, Bartlett's test
Bartlett's test
In statistics, Bartlett's test is used to test if k samples are from populations with equal variances. Equal variances across samples is called homoscedasticity or homogeneity of variances. Some statistical tests, for example the analysis of variance, assume that variances are equal across groups...
, or the Brown–Forsythe test are better tests for testing the equality of two variances. (However, all of these tests create experiment-wise Type I error inflations when conducted as a test of the assumption of homoscedasticity prior to a test of effects.) F-tests for the equality of variances can be used in practice, with care, particularly where a quick check is required, and subject to associated diagnostic checking: practical text-books suggest both graphical and formal checks of the assumption.
F-test
F-test
An F-test is any statistical test in which the test statistic has an F-distribution under the null hypothesis.It is most often used when comparing statistical models that have been fit to a data set, in order to identify the model that best fits the population from which the data were sampled. ...
s are used for other statistical tests of hypotheses, such as testing for differences in means in three or more groups, or in factorial layouts. These F-tests are generally not robust
Robust statistics
Robust statistics provides an alternative approach to classical statistical methods. The motivation is to produce estimators that are not unduly affected by small departures from model assumptions.- Introduction :...
when there are violations of the assumption that each population follows the normal distribution, particularly for small alpha levels and unbalanced layouts. However, for large alpha levels (e.g., at least 0.05) and balanced layouts, the F-test is relatively robust, although (if the normality assumption does not hold) it suffers from a loss in comparative statistical power as compared with non-parametric counterparts.
Generalization
The immediate generalization of the problem outlined above is to situations where there are more than two groups or populations, and the hypothesis is that all of the variances are equal. This is the problem treated by Hartley's testHartley's test
In statistics, Hartley's test, also known as the Fmax test or Hartley's Fmax, is used in the analysis of variance to verify that different groups have a similar variance, an assumption needed for other statistical tests.It was developed by H. O...
and Bartlett's test
Bartlett's test
In statistics, Bartlett's test is used to test if k samples are from populations with equal variances. Equal variances across samples is called homoscedasticity or homogeneity of variances. Some statistical tests, for example the analysis of variance, assume that variances are equal across groups...
.