
FOSD Program Cubes
Encyclopedia
A program in Feature Oriented Software Development (FOSD)
is
a composition of functions (program transformations): a base program (modeled by a nullary function) is composed with
increments in program functionality, called features (which are unary functions),
to produce a complex program.
A software product line (SPL) is a family of related programs.
Suppose product line PL has F0 as a base program, and F1..Fn
as features that could be added to F0. Different compositions of these functions/transformations yield different programs.
For this discussion, let
+ denote function composition. A program P in PL might have the following expression:

That is, P extends program F0 with features F1, F2, F4, and F8 in this order.
We can recast P in terms of a projection and contraction of a 1-dimensional array.
Let Fi = [F0 .. Fn] denote the array of transformations that define PL. A projection of Fi eliminates
unneeded transformations, yielding a shorter array (call it) Gi. A contraction of Gi composes each
transformation of Gi in a specific order, to yield a scalar expression. The expression for P becomes:

where the index values accomplish projection and summation is array contraction. This idea
generalizes to n-dimensional arrays that model multi-dimensional product lines.
 A multi-dimensional product line is described by multiple interacting sets of features.
A multi-dimensional product line is described by multiple interacting sets of features.
As an elementary 2D example, it is easy to create a product line of calculators, where
variants offer different sets of operations. Another variation
might offer different presentation front ends to calculators, one with no GUI, another
with a Java GUI, a third with a web GUI. These variations interact:
each GUI representation references a specific calculator operation, so each GUI
feature cannot be designed independently of its
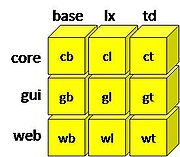
calculator feature. Such a design leads to a matrix: columns represent increments in
calculator functionality, and rows represent different presentation front-ends. Such a matrix M is shown to the right: columns allow one to pair
basic calculator functionality (base) with optional logarithmic/exponentiation (lx)
and trigonometric (tg) features. Rows allow one to pair core functionality with no
front-end (core), with optional GUI (gui) and web-based (web) front-ends.
An element Mij implements the interaction of column feature i and row feature j.
For example, the element labeled cb is a base program
that implements the core functionality of a calculator. Element gb adds code that
displays the core functionality as a GUI; element wb adds code that displays the
core functionality via the web. Similarly, element ct adds trigonometric code to the
core calculator functionality; elements gt and wt add code to display the trigonometric functionality
as a GUI and web front-ends.
A calculator is uniquely specified by two sequences
of features: one sequence defining the calculator functionality, the other the front-end.
For example, calculator C that offers both base and trig functionality in a web format
is defined by the expression:

A scalar is a kube of rank 0, a vector is a kube of rank 1, and a matrix is
rank 2. Following tensor notation: the number of indices a kube has designates
its rank. A scalar S is rank 0 (it has no indices), Vk is a vector (rank
1), Mij is a matrix (rank 2), Cijk is a cube (rank 3).
Program Cubes or program kubes are n-dimensional arrays of functions
(program transformations) that represent n-dimensional product lines.
The values along each axis
of a kube denote either a base program or a feature that could elaborate a base program.
The rank of a product line is the rank of its kube.
A program in an n-dimensional SPL is uniquely specified by n sequences of features S1..Sn, one per dimension.
The design of a program is a scalar (expression) that is formed by (1) projecting the kube
of its unneeded elements, and (2) contracting the resultant kube to a scalar:
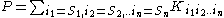
Program synthesis is evaluating the scalar expression to produce program P.
An interesting property of kube design is that the order in which dimensions are contracted does not
matter -- any permutation of dimensions during contraction will result in a different
scalar expression (i.e. a different program design), but all expressions produce the
same value (program). For example, another expression (design) to produce calculator C contracts
dimensions in the opposite order from its original specification:
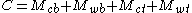
Or more generally:

The significance of program kubes is that it provides a structured way in which to
express and build multi-dimensional models of SPLs. Further, it provides scalable
specifications. If each dimension has k values, an n-kube specification of a program
requires O(kn) terms, as opposed to O(kn) kube elements that would otherwise
have to be identified and then composed. In general, kubes provide a compact way
to specify complex programs.
It is also a fundamental problem in multi-dimensional SPL design. The expression problem is an example of an SPL of rank 2. The following applications either explain/illustrate the expression problem or show how it scales to product lines of large programs. EP is really a SPL of ~30 line programs; the applications below show how these ideas scale to programs of >30K lines (a 103 increase in size).
Also, FOSD metamodels
can be viewed as special cases of program kubes.
Feature Oriented Programming
Feature Oriented Programming or Feature Oriented Software Development is a general paradigm for program synthesis in software product lines....
is
a composition of functions (program transformations): a base program (modeled by a nullary function) is composed with
increments in program functionality, called features (which are unary functions),
to produce a complex program.
A software product line (SPL) is a family of related programs.
Suppose product line PL has F0 as a base program, and F1..Fn
as features that could be added to F0. Different compositions of these functions/transformations yield different programs.
For this discussion, let
+ denote function composition. A program P in PL might have the following expression:

That is, P extends program F0 with features F1, F2, F4, and F8 in this order.
We can recast P in terms of a projection and contraction of a 1-dimensional array.
Let Fi = [F0 .. Fn] denote the array of transformations that define PL. A projection of Fi eliminates
unneeded transformations, yielding a shorter array (call it) Gi. A contraction of Gi composes each
transformation of Gi in a specific order, to yield a scalar expression. The expression for P becomes:

where the index values accomplish projection and summation is array contraction. This idea
generalizes to n-dimensional arrays that model multi-dimensional product lines.
Multi-Dimensional Product Lines

As an elementary 2D example, it is easy to create a product line of calculators, where
variants offer different sets of operations. Another variation
might offer different presentation front ends to calculators, one with no GUI, another
with a Java GUI, a third with a web GUI. These variations interact:
each GUI representation references a specific calculator operation, so each GUI
feature cannot be designed independently of its
calculator feature. Such a design leads to a matrix: columns represent increments in
calculator functionality, and rows represent different presentation front-ends. Such a matrix M is shown to the right: columns allow one to pair
basic calculator functionality (base) with optional logarithmic/exponentiation (lx)
and trigonometric (tg) features. Rows allow one to pair core functionality with no
front-end (core), with optional GUI (gui) and web-based (web) front-ends.
An element Mij implements the interaction of column feature i and row feature j.
For example, the element labeled cb is a base program
that implements the core functionality of a calculator. Element gb adds code that
displays the core functionality as a GUI; element wb adds code that displays the
core functionality via the web. Similarly, element ct adds trigonometric code to the
core calculator functionality; elements gt and wt add code to display the trigonometric functionality
as a GUI and web front-ends.
A calculator is uniquely specified by two sequences
of features: one sequence defining the calculator functionality, the other the front-end.
For example, calculator C that offers both base and trig functionality in a web format
is defined by the expression:

- Note: Each dimension is a collection of base programs and features. Not all of their compositions are meaningful. A feature modelFeature modelFeature model is a compact representation of all the products of the Software Product Line in terms of "features". Feature models are visually represented by means of feature diagrams. Feature models are widely used during the whole product line development process and are commonly used as input...
defines the legal combinations of features. Thus, each dimension would have its own feature modelFeature modelFeature model is a compact representation of all the products of the Software Product Line in terms of "features". Feature models are visually represented by means of feature diagrams. Feature models are widely used during the whole product line development process and are commonly used as input...
. It is possible that selected features along one dimension may preclude or require features along other dimensions. In any case, these feature models define the legal combinations of features in a multi-dimensional product line.
Kubes
In general, a kube is an n-dimensional array. The rank of a kube is its dimensionality.A scalar is a kube of rank 0, a vector is a kube of rank 1, and a matrix is
rank 2. Following tensor notation: the number of indices a kube has designates
its rank. A scalar S is rank 0 (it has no indices), Vk is a vector (rank
1), Mij is a matrix (rank 2), Cijk is a cube (rank 3).
Program Cubes or program kubes are n-dimensional arrays of functions
(program transformations) that represent n-dimensional product lines.
The values along each axis
of a kube denote either a base program or a feature that could elaborate a base program.
The rank of a product line is the rank of its kube.
- Note: program kubes are inspired by tensorsTensorTensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
and data cubesOLAP cubeAn OLAP cube is a data structure that allows fast analysis of data. It can also be defined as the capability of manipulating and analyzing data from multiple perspectives...
in databases. The primary difference is that data cube elements are numerical values that are added during kube contraction; program kube elements are transformations that are composed. Both use tensorTensorTensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
notations and terminology, although kubes satisfy few algebraic properties of tensors.
A program in an n-dimensional SPL is uniquely specified by n sequences of features S1..Sn, one per dimension.
The design of a program is a scalar (expression) that is formed by (1) projecting the kube
of its unneeded elements, and (2) contracting the resultant kube to a scalar:
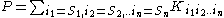
Program synthesis is evaluating the scalar expression to produce program P.
An interesting property of kube design is that the order in which dimensions are contracted does not
matter -- any permutation of dimensions during contraction will result in a different
scalar expression (i.e. a different program design), but all expressions produce the
same value (program). For example, another expression (design) to produce calculator C contracts
dimensions in the opposite order from its original specification:
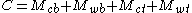
Or more generally:

- Note: Underlying kube designs is a commuting diagramCommutative diagramIn mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
, such that there are an exponential number of paths from the empty program 0 to program P. Each path denotes a particular contraction of a kube, and corresponds to a unique incremental design of P. Included among these paths are kube aggregations that contract kubes using different dimensional orders.
The significance of program kubes is that it provides a structured way in which to
express and build multi-dimensional models of SPLs. Further, it provides scalable
specifications. If each dimension has k values, an n-kube specification of a program
requires O(kn) terms, as opposed to O(kn) kube elements that would otherwise
have to be identified and then composed. In general, kubes provide a compact way
to specify complex programs.
Applications
The expression problem (EP) (a.k.a. the extensibility problem) is a fundamental problem in programming languages aimed at type systems that can add new classes and methods to a program in a type-safe manner.It is also a fundamental problem in multi-dimensional SPL design. The expression problem is an example of an SPL of rank 2. The following applications either explain/illustrate the expression problem or show how it scales to product lines of large programs. EP is really a SPL of ~30 line programs; the applications below show how these ideas scale to programs of >30K lines (a 103 increase in size).
- [ftp://ftp.cs.utexas.edu/pub/predator/ECOOP2005.pdf Expression Problem]
- Illustration of Small Expression Problem
- [ftp://ftp.cs.utexas.edu/pub/predator/Origami.pdf Extensible IDEs]
- [ftp://ftp.cs.utexas.edu/pub/predator/OrigamiMDSC.pdf Multi-Dimensional Separation of Concerns]
- [ftp://ftp.cs.utexas.edu/pub/predator/TSE-AHEAD.pdf Calculator Product Line]
Also, FOSD metamodels
FOSD metamodels
Feature Oriented Software Development is a general paradigm for program synthesis in software product lines, where a model of a product line is a tuple of 0-ary and 1-ary functions...
can be viewed as special cases of program kubes.
See also
- Feature Oriented ProgrammingFeature Oriented ProgrammingFeature Oriented Programming or Feature Oriented Software Development is a general paradigm for program synthesis in software product lines....
-- basic overview - FOSD MetamodelsFOSD metamodelsFeature Oriented Software Development is a general paradigm for program synthesis in software product lines, where a model of a product line is a tuple of 0-ary and 1-ary functions...
-- product lines of product lines - FOSD Feature AlgebrasFOSD Feature AlgebrasFeature Oriented Programming or Feature Oriented Software Development is a general paradigm for program synthesis in software product lines. Please read the Feature Oriented Programming page that explains how an FOSD model of a product line is a tuple of 0-ary and 1-ary functions...
-- operations from which FOSD features (0-ary and 1-ary) functions are defined - FOSD Feature InteractionsFOSD Feature InteractionsFeature Oriented Programming or Feature Oriented Software Development is a general paradigm for program synthesis in software product lines. The building blocks of programs are features...
-- general concepts for feature interactions

