
Fabius function
Encyclopedia
In mathematics, the Fabius function is an example of an infinitely differentiable function that is not analytic
anywhere, found by .
The Fabius function is defined on the unit interval, and is given by the probability distribution
of
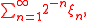
where the ξn are independent uniformly distributed
random variable
s on the unit interval
.
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
anywhere, found by .
The Fabius function is defined on the unit interval, and is given by the probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of
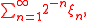
where the ξn are independent uniformly distributed
Uniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s on the unit interval
Unit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
.

