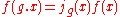Factor of automorphy
Encyclopedia
In mathematics
, the notion of factor of automorphy arises for a group
acting
on a complex-analytic manifold. Suppose a group
acts on a complex-analytic manifold 
. Then, 
also acts on the space of holomorphic function
s from
to the complex numbers. A function 
is termed an automorphic form
if the following holds:
where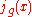
is an everywhere nonzero holomorphic function. Equivalently, an automorphic form is a function whose divisor is invariant under the action of 
.
The factor of automorphy for the automorphic form
is the function 
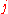. An automorphic function is an automorphic form for which 
is the identity.
Some facts about factors of automorphy:
Relation between factors of automorphy and other notions:
The specific case of
a subgroup of SL(2, R), acting on the upper half-plane, is treated in the article on automorphic factor
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the notion of factor of automorphy arises for a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
acting
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on a complex-analytic manifold. Suppose a group
acts on a complex-analytic manifold . Then, also acts on the space of holomorphic functionHolomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s from
to the complex numbers. A function is termed an automorphic formAutomorphic form
In mathematics, the general notion of automorphic form is the extension to analytic functions, perhaps of several complex variables, of the theory of modular forms...
if the following holds:
where
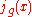is an everywhere nonzero holomorphic function. Equivalently, an automorphic form is a function whose divisor is invariant under the action of .The factor of automorphy for the automorphic form
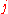is the function . An automorphic function is an automorphic form for which is the identity.Some facts about factors of automorphy:
- Every factor of automorphy is a cocycleCocycleA cocycle refers to any one of the following:*A closed cochain in algebraic topology is called a cocycle.*A particular type of map in an autonomous dynamical system; see Oseledec theorem....
for the action of
on the multiplicative group of everywhere nonzero holomorphic functions. - The factor of automorphy is a coboundary if and only if it arises from an everywhere nonzero automorphic form.
- For a given factor of automorphy, the space of automorphic forms is a vector space.
- The pointwise product of two automorphic forms is an automorphic form corresponding to the product of the corresponding factors of automorphy.
Relation between factors of automorphy and other notions:
- Let
be a lattice in a Lie group 
. Then, a factor of automorphy for 
corresponds to a line bundleLine bundleIn mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
on the quotient group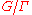
. Further, the automorphic forms for a given factor of automorphy correspond to sections of the corresponding line bundle.
The specific case of
a subgroup of SL(2, R), acting on the upper half-plane, is treated in the article on automorphic factorAutomorphic factor
In mathematics, an automorphic factor is a certain type of analytic function, defined on subgroups of SL, appearing in the theory of modular forms...
s.