Fair division
Encyclopedia
Fair division, also known as the cake-cutting problem, is the problem of dividing a resource in such a way that all recipients believe that they have received a fair amount. The problem is easier when recipients have different measures of value of the parts of the resource: in the "cake cutting" version, one recipient may like marzipan
, another prefers cherries, and so on—then, and only then, the n recipients may get even more than what would be one n-th of the value of the "cake" for each of them. On the other hand, the presence of different measures opens a vast potential for many challenging questions and directions of further research.
There are a number of variants of the problem. The definition of 'fair' may simply mean that they get at least their fair proportion
, or harder requirements like envy-free
ness may also need to be satisfied. The theoretical algorithms mainly deal with goods that can be divided without losing value. The division of indivisible goods, as in for instance a divorce, is a major practical problem. Chore division
is a variant where the goods are undesirable.
Fair division is often used to refer to just the simplest variant. That version is referred to here as proportional division
or simple fair division.
Most of what is normally called a fair division is not considered so by the theory because of the use of arbitration
. This kind of situation happens quite often with mathematical theories named after real life problems. The decisions in the Talmud
on entitlement
when an estate is bankrupt reflect some quite complex ideas about fairness, and most people would consider them fair. However they are the result of legal debates by rabbis rather than divisions according to the valuations of the claimants.
to them. The central tenet of fair division is that such a division should be performed by the players themselves, maybe using a mediator
but certainly not an arbiter
as only the players really know how they value the goods.
The theory of fair division provides explicit criteria for various different types of fairness. Its aim is to provide procedures (algorithm
s) to achieve a fair division, or prove their impossibility, and study the properties of such divisions both in theory and in real life.
The assumptions about the valuation of the goods or resources are:
Indivisible parts make the theory much more complex. An example of this would be where a car and a motorcycle have to be shared. This is also an example of where the values may not add up nicely, as either can be used as transport. The use of money can make such problems much easier.
The criteria of a fair division are stated in terms of a players valuations, their level of entitlement
, and the results of a fair division procedure. The valuations of the other players are not involved in the criteria. Differing entitlements can normally be represented by having a different number of proxy players for each player but sometimes the criteria specify something different.
In the real world of course people sometimes have a very accurate idea of how the other players value the goods and they may care very much about it. The case where they have complete knowledge of each other's valuations can be modeled by game theory
. Partial knowledge is very hard to model. A major part of the practical side of fair division is the devising and study of procedures that work well despite such partial knowledge or small mistakes.
A fair division procedure
lists actions to be performed by the players in terms of the visible data and their valuations. A valid procedure is one that guarantees a fair division for every player who acts rationally according to their valuation. Where an action depends on a player's valuation the procedure is describing the strategy
a rational player will follow. A player may act as if a piece had a different value but must be consistent. For instance if a procedure says the first player cuts the cake in two equal parts then the second player chooses a piece, then the first player cannot claim that the second player got more.
What the players do is:
It is assumed the aim of each player is to maximize the minimum amount they might get, or in other words, to achieve the maximin
.
Procedures can be divided into finite and continuous procedures. A finite procedure would for instance only involve one person at a time cutting or marking a cake. Continuous procedures involve things like one player moving a knife
and the other saying stop. Another type of continuous procedure involves a person assigning a value to every part of the cake.
method. One person divides the resource into what they believe are equal halves, and the other person chooses the "half" they prefer. Thus, the person making the division has an incentive to divide as fairly as possible: for if they do not, they will likely receive an undesirable portion. This solution gives a proportional
and envy-free
division.
The article on divide and choose
describes why the procedure is not equitable. More complex procedures like the adjusted winner procedure
are designed to cope with indivisible goods and to be more equitable in a practical context.
Austin's moving-knife procedure
gives an exact division for two players. The first player places two knives over the cake such that one knife is at the left side of the cake, and one is further right; half of the cake lies between the knives. He then moves the knives right, always ensuring there is half the cake – by his valuation – between the knives. If he reaches the right side of the cake, the leftmost knife must be where the rightmost knife started off. The second player stops the knives when he thinks there is half the cake between the knives. There will always be a point at which this happens, because of the intermediate value theorem
.
The surplus procedure
(SP) achieves a form of equitability called proportional equitability. This procedure is strategy proof and can be generalized to more than two people.
Proportional
division is the easiest and the article describes some procedures which can be applied with any number of players. Finding the minimum number of cuts needed is an interesting mathematical problem.
Envy-free
division was first solved for the 3 player case in 1960 independently by John Selfridge of Northern Illinois University
and John Horton Conway
at Cambridge University. The best algorithm uses at most 5 cuts.
The Brams-Taylor procedure was the first cake-cutting procedure for four or more players that produced an envy-free
division of cake for any number of persons and was published by Steven Brams
and Alan Taylor
in 1995. This number of cuts that might be required by this procedure is unbounded. A bounded moving knife procedure for 4 players was found in 1997.
There are no discrete algorithms for an exact division even for two players, a moving knife procedure is the best that can be done. There are no exact division algorithms for 3 or more players but there are 'near exact' algorithms which are also envy-free and can achieve any desired degree of accuracy.
A generalization of the surplus procedure
called the equitable procedure (EP) achieves a form of equitability. Equitability and envy-freeness can be incompatible for 3 or more players.
(usually in a sequence of steps). Moving-knife procedure
s, on the other hand, allow continuous movement and can let players call "stop" at any point.
A variant of the fair division problem is chore division
: this is the "dual" to the cake-cutting problem in which an undesirable object is to be distributed amongst the players. The canonical example is a set of chores that the players between them must do. Note that "I cut, you choose" works for chore division. A basic theorem for many person problems is the Rental Harmony Theorem by Francis Su. An interesting application of the Rental Harmony Theorem can be found in the international trade theory.
Sperner's Lemma
can be used to get as close an approximation as desired to an envy-free solutions for many players. The algorithm gives a fast and practical way of solving some fair division problems.
The division of property, as happens for example in divorce or inheritance, normally contains indivisible items which must be fairly distributed between players, possibly with cash adjustments (such pieces are referred to as atoms).
A common requirement for the division of land is that the pieces be connected
, i.e. only whole pieces and not fragments are allowed. For example the division of Berlin after World War 2 resulted in four connected parts.
A consensus halving is where a number of people agree that a resource has been evenly split in two, this is described in exact division
.
, the cake-cutting problem had been one of the most important open problems in 20th century mathematics, when the most important variant of the problem was finally solved with the Brams-Taylor procedure by Steven Brams
and Alan Taylor
in 1995.
Divide and choose
has probably been used since prehistory . The related activities of bargaining
and barter
are also ancient. Negotiation
s involving more than two people are also quite common, the Potsdam Conference
is a notable recent example.
The theory of fair division dates back only to the end of the second world war. It was devised by a group of Polish
mathematicians, Hugo Steinhaus
, Bronisław Knaster and Stefan Banach
, who used to meet in the Scottish Café
in Lvov (then in Poland). A proportional (fair division)
division for any number of players called 'last-diminisher' was devised in 1944. This was attributed to Banach and Knaster by Steinhaus when he made the problem public for the first time at a meeting of the Econometric Society
in Washington D.C. on 17 September 1947. At that meeting he also proposed the problem of finding the smallest number of cuts necessary for such divisions.
Envy-free
division was first solved for the 3 player case in 1960 independently by John Selfridge of Northern Illinois University
and John Horton Conway
at Cambridge University, the algorithm was first published in the 'Mathematical Games' column by Martin Gardner
in Scientific American
.
Envy-free division for 4 or more players was a difficult open problem of the twentieth century. The first cake-cutting procedure that produced an envy-free
division of cake for any number of persons was first published by Steven Brams
and Alan Taylor
in 1995.
A major advance on equitable division was made in 2006 by Steven J. Brams
, Michael A. Jones, and Christian Klamler.
Marzipan
Marzipan is a confection consisting primarily of sugar and almond meal. Persipan is a similar, yet less expensive product, in which the almonds are replaced by apricot or peach kernels...
, another prefers cherries, and so on—then, and only then, the n recipients may get even more than what would be one n-th of the value of the "cake" for each of them. On the other hand, the presence of different measures opens a vast potential for many challenging questions and directions of further research.
There are a number of variants of the problem. The definition of 'fair' may simply mean that they get at least their fair proportion
Proportional (fair division)
Proportional division or simple fair division is the original and simplest problem in fair division. Fair division problems are also called cake-cutting problems. A proportional division of a cake between N people would ensure each of them got at least 1/N of the cake by their own valuation...
, or harder requirements like envy-free
Envy-free
In mathematical sociology and especially game theory, envy-free is a property of certain fair division algorithms for a divisible heterogeneous good over which different players may have different preferences....
ness may also need to be satisfied. The theoretical algorithms mainly deal with goods that can be divided without losing value. The division of indivisible goods, as in for instance a divorce, is a major practical problem. Chore division
Chore division
In problems of fair division, a resource is to be divided amongst a finite number of players; the resource is assumed to be desirable, and more is assumed to be better...
is a variant where the goods are undesirable.
Fair division is often used to refer to just the simplest variant. That version is referred to here as proportional division
Proportional (fair division)
Proportional division or simple fair division is the original and simplest problem in fair division. Fair division problems are also called cake-cutting problems. A proportional division of a cake between N people would ensure each of them got at least 1/N of the cake by their own valuation...
or simple fair division.
Most of what is normally called a fair division is not considered so by the theory because of the use of arbitration
Arbitration
Arbitration, a form of alternative dispute resolution , is a legal technique for the resolution of disputes outside the courts, where the parties to a dispute refer it to one or more persons , by whose decision they agree to be bound...
. This kind of situation happens quite often with mathematical theories named after real life problems. The decisions in the Talmud
Talmud
The Talmud is a central text of mainstream Judaism. It takes the form of a record of rabbinic discussions pertaining to Jewish law, ethics, philosophy, customs and history....
on entitlement
Entitlement (fair division)
Entitlement in fair division describes that proportion of the resources or goods to be divided that a player can expect to receive. The idea is based on the normal idea of entitlement...
when an estate is bankrupt reflect some quite complex ideas about fairness, and most people would consider them fair. However they are the result of legal debates by rabbis rather than divisions according to the valuations of the claimants.

Assumptions
Fair division is a mathematical theory based on an idealization of a real life problem. The real life problem is the one of dividing goods or resources fairly between people, the 'players', who have an entitlementEntitlement
An entitlement is a guarantee of access to benefits based on established rights or by legislation. A "right" is itself an entitlement associated with a moral or social principle, such that an "entitlement" is a provision made in accordance with legal framework of a society...
to them. The central tenet of fair division is that such a division should be performed by the players themselves, maybe using a mediator
Mediation
Mediation, as used in law, is a form of alternative dispute resolution , a way of resolving disputes between two or more parties. A third party, the mediator, assists the parties to negotiate their own settlement...
but certainly not an arbiter
Arbitration
Arbitration, a form of alternative dispute resolution , is a legal technique for the resolution of disputes outside the courts, where the parties to a dispute refer it to one or more persons , by whose decision they agree to be bound...
as only the players really know how they value the goods.
The theory of fair division provides explicit criteria for various different types of fairness. Its aim is to provide procedures (algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s) to achieve a fair division, or prove their impossibility, and study the properties of such divisions both in theory and in real life.
The assumptions about the valuation of the goods or resources are:
- Each player has their own opinion of the value of each part of the goods or resources
- The value to a player of any allocation is the sum of his valuations of each part. Often just requiring the valuations be weakly additiveWeakly additiveIn fair division, a set of preferences is weakly additiveif the following condition is met:Weak additivity is often a realistic assumption when dividing up goods between claimants, and simplifies the mathematics of certain fair division problems considerably.-Use of weak additivity:Some procedures...
is enough. - In the basic theory the goods can be divided into parts with arbitrarily small value.
Indivisible parts make the theory much more complex. An example of this would be where a car and a motorcycle have to be shared. This is also an example of where the values may not add up nicely, as either can be used as transport. The use of money can make such problems much easier.
The criteria of a fair division are stated in terms of a players valuations, their level of entitlement
Entitlement (fair division)
Entitlement in fair division describes that proportion of the resources or goods to be divided that a player can expect to receive. The idea is based on the normal idea of entitlement...
, and the results of a fair division procedure. The valuations of the other players are not involved in the criteria. Differing entitlements can normally be represented by having a different number of proxy players for each player but sometimes the criteria specify something different.
In the real world of course people sometimes have a very accurate idea of how the other players value the goods and they may care very much about it. The case where they have complete knowledge of each other's valuations can be modeled by game theory
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
. Partial knowledge is very hard to model. A major part of the practical side of fair division is the devising and study of procedures that work well despite such partial knowledge or small mistakes.
A fair division procedure
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
lists actions to be performed by the players in terms of the visible data and their valuations. A valid procedure is one that guarantees a fair division for every player who acts rationally according to their valuation. Where an action depends on a player's valuation the procedure is describing the strategy
Strategy
Strategy, a word of military origin, refers to a plan of action designed to achieve a particular goal. In military usage strategy is distinct from tactics, which are concerned with the conduct of an engagement, while strategy is concerned with how different engagements are linked...
a rational player will follow. A player may act as if a piece had a different value but must be consistent. For instance if a procedure says the first player cuts the cake in two equal parts then the second player chooses a piece, then the first player cannot claim that the second player got more.
What the players do is:
- Agree on their criteria for a fair division
- Select a valid procedure and follow its rules
It is assumed the aim of each player is to maximize the minimum amount they might get, or in other words, to achieve the maximin
Minimax
Minimax is a decision rule used in decision theory, game theory, statistics and philosophy for minimizing the possible loss for a worst case scenario. Alternatively, it can be thought of as maximizing the minimum gain...
.
Procedures can be divided into finite and continuous procedures. A finite procedure would for instance only involve one person at a time cutting or marking a cake. Continuous procedures involve things like one player moving a knife
Moving-knife procedure
In the mathematics of social science, and especially game theory, a moving-knife procedure is a type of solution to the fair division problem. The canonical example is the division of a cake using a knife....
and the other saying stop. Another type of continuous procedure involves a person assigning a value to every part of the cake.
Criteria for a fair division
There are a number of widely used criteria for a fair division. Some of these conflict with each other but often they can be combined. The criteria described here are only for when each player is entitled to the same amount.- A proportionalProportional (fair division)Proportional division or simple fair division is the original and simplest problem in fair division. Fair division problems are also called cake-cutting problems. A proportional division of a cake between N people would ensure each of them got at least 1/N of the cake by their own valuation...
or simple fair division guarantees each player gets his fair share. For instance if three people divide up a cake each gets at least a third by their own valuation.
- An envy-freeEnvy-freeIn mathematical sociology and especially game theory, envy-free is a property of certain fair division algorithms for a divisible heterogeneous good over which different players may have different preferences....
division guarantees no-one will want somebody else's share more than their own.
- An exact divisionExact divisionIn game theory, an exact or even division is a type of fair division where all the players believe everyone received the same amount.There is no finite fair division procedure for exact division of divisible goods. However there are moving knife procedures for two players...
is one where every player thinks everyone received exactly their fair share, no more and no less.
- An efficient or Pareto optimal division ensures no other allocation would make someone better off without making someone else worse off. The term efficiency comes from the economicsEconomicsEconomics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
idea of the efficient market. A division where one player gets everything is optimal by this definition so on its own this does not guarantee even a fair share.
- An equitableEquity (economics)Equity is the concept or idea of fairness in economics, particularly as to taxation or welfare economics. More specifically it may refer to equal life chances regardless of identity, to provide all citizens with a basic minimum of income/goods/services or to increase funds and commitment for...
division is one where the proportion of the cake a player receives by their own valuation is the same for every player. This is a difficult aim as players need not be truthful if asked their valuation.
Two players
For two people there is a simple solution which is commonly employed. This is the so-called divide and chooseDivide and choose
In problems of fair division, divide and choose is a two-party proportional envy-free allocation protocol. The protocol also works for dividing an undesirable, as in chore division....
method. One person divides the resource into what they believe are equal halves, and the other person chooses the "half" they prefer. Thus, the person making the division has an incentive to divide as fairly as possible: for if they do not, they will likely receive an undesirable portion. This solution gives a proportional
Proportional (fair division)
Proportional division or simple fair division is the original and simplest problem in fair division. Fair division problems are also called cake-cutting problems. A proportional division of a cake between N people would ensure each of them got at least 1/N of the cake by their own valuation...
and envy-free
Envy-free
In mathematical sociology and especially game theory, envy-free is a property of certain fair division algorithms for a divisible heterogeneous good over which different players may have different preferences....
division.
The article on divide and choose
Divide and choose
In problems of fair division, divide and choose is a two-party proportional envy-free allocation protocol. The protocol also works for dividing an undesirable, as in chore division....
describes why the procedure is not equitable. More complex procedures like the adjusted winner procedure
Adjusted Winner procedure
In problems of fair division, the adjusted winner procedure is used to partition a bundle of goods between two players in such a way as to minimize envy and maximize efficiency and equitability...
are designed to cope with indivisible goods and to be more equitable in a practical context.
Austin's moving-knife procedure
Moving-knife procedure
In the mathematics of social science, and especially game theory, a moving-knife procedure is a type of solution to the fair division problem. The canonical example is the division of a cake using a knife....
gives an exact division for two players. The first player places two knives over the cake such that one knife is at the left side of the cake, and one is further right; half of the cake lies between the knives. He then moves the knives right, always ensuring there is half the cake – by his valuation – between the knives. If he reaches the right side of the cake, the leftmost knife must be where the rightmost knife started off. The second player stops the knives when he thinks there is half the cake between the knives. There will always be a point at which this happens, because of the intermediate value theorem
Intermediate value theorem
In mathematical analysis, the intermediate value theorem states that for each value between the least upper bound and greatest lower bound of the image of a continuous function there is at least one point in its domain that the function maps to that value....
.
The surplus procedure
Surplus procedure
The surplus procedure is a fair division protocol for dividing goods in a way that achieves proportional equitability. It can be generalized to more than 2 people and is strategyproof. For 3 or more people it is not always possible to achieve a division that is both equitabile and envy-free.The...
(SP) achieves a form of equitability called proportional equitability. This procedure is strategy proof and can be generalized to more than two people.
Many players
Fair division with three or more players is considerably more complex than the two player case.Proportional
Proportional (fair division)
Proportional division or simple fair division is the original and simplest problem in fair division. Fair division problems are also called cake-cutting problems. A proportional division of a cake between N people would ensure each of them got at least 1/N of the cake by their own valuation...
division is the easiest and the article describes some procedures which can be applied with any number of players. Finding the minimum number of cuts needed is an interesting mathematical problem.
Envy-free
Envy-free
In mathematical sociology and especially game theory, envy-free is a property of certain fair division algorithms for a divisible heterogeneous good over which different players may have different preferences....
division was first solved for the 3 player case in 1960 independently by John Selfridge of Northern Illinois University
Northern Illinois University
Northern Illinois University is a state university and research institution located in DeKalb, Illinois, with satellite centers in Hoffman Estates, Naperville, Rockford, and Oregon. It was originally founded as Northern Illinois State Normal School on May 22, 1895 by Illinois Governor John P...
and John Horton Conway
John Horton Conway
John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
at Cambridge University. The best algorithm uses at most 5 cuts.
The Brams-Taylor procedure was the first cake-cutting procedure for four or more players that produced an envy-free
Envy-free
In mathematical sociology and especially game theory, envy-free is a property of certain fair division algorithms for a divisible heterogeneous good over which different players may have different preferences....
division of cake for any number of persons and was published by Steven Brams
Steven Brams
Steven J. Brams is a game theorist and political scientist at the New York University Department of Politics. Brams is best known for using the techniques of game theory and public choice to research voting systems and fair division. He is one of the independent discoverers of approval voting...
and Alan Taylor
Alan D. Taylor
Alan Dana Taylor is a mathematician who, with Steven Brams, solved the problem of envy-free fair division for an arbitrary number of people with the Brams–Taylor procedure.Taylor received his Ph.D...
in 1995. This number of cuts that might be required by this procedure is unbounded. A bounded moving knife procedure for 4 players was found in 1997.
There are no discrete algorithms for an exact division even for two players, a moving knife procedure is the best that can be done. There are no exact division algorithms for 3 or more players but there are 'near exact' algorithms which are also envy-free and can achieve any desired degree of accuracy.
A generalization of the surplus procedure
Surplus procedure
The surplus procedure is a fair division protocol for dividing goods in a way that achieves proportional equitability. It can be generalized to more than 2 people and is strategyproof. For 3 or more people it is not always possible to achieve a division that is both equitabile and envy-free.The...
called the equitable procedure (EP) achieves a form of equitability. Equitability and envy-freeness can be incompatible for 3 or more players.
Variants
Some cake-cutting procedures are discrete, whereby players make cuts with a knifeKnife
A knife is a cutting tool with an exposed cutting edge or blade, hand-held or otherwise, with or without a handle. Knives were used at least two-and-a-half million years ago, as evidenced by the Oldowan tools...
(usually in a sequence of steps). Moving-knife procedure
Moving-knife procedure
In the mathematics of social science, and especially game theory, a moving-knife procedure is a type of solution to the fair division problem. The canonical example is the division of a cake using a knife....
s, on the other hand, allow continuous movement and can let players call "stop" at any point.
A variant of the fair division problem is chore division
Chore division
In problems of fair division, a resource is to be divided amongst a finite number of players; the resource is assumed to be desirable, and more is assumed to be better...
: this is the "dual" to the cake-cutting problem in which an undesirable object is to be distributed amongst the players. The canonical example is a set of chores that the players between them must do. Note that "I cut, you choose" works for chore division. A basic theorem for many person problems is the Rental Harmony Theorem by Francis Su. An interesting application of the Rental Harmony Theorem can be found in the international trade theory.
Sperner's Lemma
Sperner's lemma
In mathematics, Sperner's lemma is a combinatorial analog of the Brouwer fixed point theorem, which follows from it. Sperner's lemma states that every Sperner coloring of a triangulation of an n-dimensional simplex contains a cell colored with a complete set of colors...
can be used to get as close an approximation as desired to an envy-free solutions for many players. The algorithm gives a fast and practical way of solving some fair division problems.
The division of property, as happens for example in divorce or inheritance, normally contains indivisible items which must be fairly distributed between players, possibly with cash adjustments (such pieces are referred to as atoms).
A common requirement for the division of land is that the pieces be connected
Connectedness
In mathematics, connectedness is used to refer to various properties meaning, in some sense, "all one piece". When a mathematical object has such a property, we say it is connected; otherwise it is disconnected...
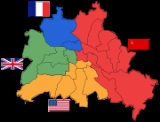
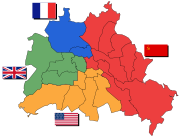
, i.e. only whole pieces and not fragments are allowed. For example the division of Berlin after World War 2 resulted in four connected parts.
A consensus halving is where a number of people agree that a resource has been evenly split in two, this is described in exact division
Exact division
In game theory, an exact or even division is a type of fair division where all the players believe everyone received the same amount.There is no finite fair division procedure for exact division of divisible goods. However there are moving knife procedures for two players...
.
History
According to Sol GarfunkelSol Garfunkel
Solomon "Sol" Garfunkel is an American mathematician who has focused his career on mathematics education and is best known for his mathematical television series For All Practical Purposes....
, the cake-cutting problem had been one of the most important open problems in 20th century mathematics, when the most important variant of the problem was finally solved with the Brams-Taylor procedure by Steven Brams
Steven Brams
Steven J. Brams is a game theorist and political scientist at the New York University Department of Politics. Brams is best known for using the techniques of game theory and public choice to research voting systems and fair division. He is one of the independent discoverers of approval voting...
and Alan Taylor
Alan D. Taylor
Alan Dana Taylor is a mathematician who, with Steven Brams, solved the problem of envy-free fair division for an arbitrary number of people with the Brams–Taylor procedure.Taylor received his Ph.D...
in 1995.
Divide and choose
Divide and choose
In problems of fair division, divide and choose is a two-party proportional envy-free allocation protocol. The protocol also works for dividing an undesirable, as in chore division....
has probably been used since prehistory . The related activities of bargaining
Bargaining
Bargaining or haggling is a type of negotiation in which the buyer and seller of a good or service dispute the price which will be paid and the exact nature of the transaction that will take place, and eventually come to an agreement. Bargaining is an alternative pricing strategy to fixed prices...
and barter
Barter
Barter is a method of exchange by which goods or services are directly exchanged for other goods or services without using a medium of exchange, such as money. It is usually bilateral, but may be multilateral, and usually exists parallel to monetary systems in most developed countries, though to a...
are also ancient. Negotiation
Negotiation
Negotiation is a dialogue between two or more people or parties, intended to reach an understanding, resolve point of difference, or gain advantage in outcome of dialogue, to produce an agreement upon courses of action, to bargain for individual or collective advantage, to craft outcomes to satisfy...
s involving more than two people are also quite common, the Potsdam Conference
Potsdam Conference
The Potsdam Conference was held at Cecilienhof, the home of Crown Prince Wilhelm Hohenzollern, in Potsdam, occupied Germany, from 16 July to 2 August 1945. Participants were the Soviet Union, the United Kingdom, and the United States...
is a notable recent example.
The theory of fair division dates back only to the end of the second world war. It was devised by a group of Polish
Poland
Poland , officially the Republic of Poland , is a country in Central Europe bordered by Germany to the west; the Czech Republic and Slovakia to the south; Ukraine, Belarus and Lithuania to the east; and the Baltic Sea and Kaliningrad Oblast, a Russian exclave, to the north...
mathematicians, Hugo Steinhaus
Hugo Steinhaus
Władysław Hugo Dionizy Steinhaus was a Polish mathematician and educator. Steinhaus obtained his PhD under David Hilbert at Göttingen University in 1911 and later became a professor at the University of Lwów, where he helped establish what later became known as the Lwów School of Mathematics...
, Bronisław Knaster and Stefan Banach
Stefan Banach
Stefan Banach was a Polish mathematician who worked in interwar Poland and in Soviet Ukraine. He is generally considered to have been one of the 20th century's most important and influential mathematicians....
, who used to meet in the Scottish Café
Scottish Café
The Scottish Café was the café in Lwów where, in the 1930s and 1940s, mathematicians from the Lwów School collaboratively discussed research problems, particularly in functional analysis and topology....
in Lvov (then in Poland). A proportional (fair division)
Proportional (fair division)
Proportional division or simple fair division is the original and simplest problem in fair division. Fair division problems are also called cake-cutting problems. A proportional division of a cake between N people would ensure each of them got at least 1/N of the cake by their own valuation...
division for any number of players called 'last-diminisher' was devised in 1944. This was attributed to Banach and Knaster by Steinhaus when he made the problem public for the first time at a meeting of the Econometric Society
Econometric Society
The Econometric Society is an international society for the advancement of economic theory in its relation with statistics and mathematics. It was founded on December 29, 1930 at the Stalton Hotel in Cleveland, Ohio....
in Washington D.C. on 17 September 1947. At that meeting he also proposed the problem of finding the smallest number of cuts necessary for such divisions.
Envy-free
Envy-free
In mathematical sociology and especially game theory, envy-free is a property of certain fair division algorithms for a divisible heterogeneous good over which different players may have different preferences....
division was first solved for the 3 player case in 1960 independently by John Selfridge of Northern Illinois University
Northern Illinois University
Northern Illinois University is a state university and research institution located in DeKalb, Illinois, with satellite centers in Hoffman Estates, Naperville, Rockford, and Oregon. It was originally founded as Northern Illinois State Normal School on May 22, 1895 by Illinois Governor John P...
and John Horton Conway
John Horton Conway
John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
at Cambridge University, the algorithm was first published in the 'Mathematical Games' column by Martin Gardner
Martin Gardner
Martin Gardner was an American mathematics and science writer specializing in recreational mathematics, but with interests encompassing micromagic, stage magic, literature , philosophy, scientific skepticism, and religion...
in Scientific American
Scientific American
Scientific American is a popular science magazine. It is notable for its long history of presenting science monthly to an educated but not necessarily scientific public, through its careful attention to the clarity of its text as well as the quality of its specially commissioned color graphics...
.
Envy-free division for 4 or more players was a difficult open problem of the twentieth century. The first cake-cutting procedure that produced an envy-free
Envy-free
In mathematical sociology and especially game theory, envy-free is a property of certain fair division algorithms for a divisible heterogeneous good over which different players may have different preferences....
division of cake for any number of persons was first published by Steven Brams
Steven Brams
Steven J. Brams is a game theorist and political scientist at the New York University Department of Politics. Brams is best known for using the techniques of game theory and public choice to research voting systems and fair division. He is one of the independent discoverers of approval voting...
and Alan Taylor
Alan D. Taylor
Alan Dana Taylor is a mathematician who, with Steven Brams, solved the problem of envy-free fair division for an arbitrary number of people with the Brams–Taylor procedure.Taylor received his Ph.D...
in 1995.
A major advance on equitable division was made in 2006 by Steven J. Brams
Steven Brams
Steven J. Brams is a game theorist and political scientist at the New York University Department of Politics. Brams is best known for using the techniques of game theory and public choice to research voting systems and fair division. He is one of the independent discoverers of approval voting...
, Michael A. Jones, and Christian Klamler.
In popular culture
- In Numb3rsNUMB3RSNumb3rs is an American television drama which premiered on CBS on January 23, 2005, and concluded on March 12, 2010. The series was created by Nicolas Falacci and Cheryl Heuton, and follows FBI Special Agent Don Eppes and his mathematical genius brother, Charlie Eppes , who helps Don solve crimes...
season 3 episode "One Hour", Charlie talks about the cake-cutting problem as applied to the amount of money a kidnapper was demanding. - Hugo SteinhausHugo SteinhausWładysław Hugo Dionizy Steinhaus was a Polish mathematician and educator. Steinhaus obtained his PhD under David Hilbert at Göttingen University in 1911 and later became a professor at the University of Lwów, where he helped establish what later became known as the Lwów School of Mathematics...
wrote about a number of variants of fair division in his book Mathematical Snapshots. In his book he says a special three-person version of fair division was devised by G. Krochmainy in Berdechów in 1944 and another by Mrs L Kott. - Martin GardnerMartin GardnerMartin Gardner was an American mathematics and science writer specializing in recreational mathematics, but with interests encompassing micromagic, stage magic, literature , philosophy, scientific skepticism, and religion...
and Ian StewartIan Stewart (mathematician)Ian Nicholas Stewart FRS is a professor of mathematics at the University of Warwick, England, and a widely known popular-science and science-fiction writer. He is the first recipient of the , awarded jointly by the LMS and the IMA for his work on promoting mathematics.-Biography:Stewart was born...
have both published books with sections about the problem. Martin Gardner introduced the chore division form of the problem. Ian Stewart has popularized the fair division problem with his articles in Scientific AmericanScientific AmericanScientific American is a popular science magazine. It is notable for its long history of presenting science monthly to an educated but not necessarily scientific public, through its careful attention to the clarity of its text as well as the quality of its specially commissioned color graphics...
and New ScientistNew ScientistNew Scientist is a weekly non-peer-reviewed English-language international science magazine, which since 1996 has also run a website, covering recent developments in science and technology for a general audience. Founded in 1956, it is published by Reed Business Information Ltd, a subsidiary of...
. - A Dinosaur ComicsDinosaur ComicsDinosaur Comics is a constrained webcomic by Canadian writer Ryan North. It is also known as "Qwantz", after the site's domain name, "qwantz.com". The first comic was posted on 1 February 2003, though there were earlier prototypes. Dinosaur Comics has also been printed in two collections and in a...
strip is based on the cake-cutting problem.
See also
- Alan D. TaylorAlan D. TaylorAlan Dana Taylor is a mathematician who, with Steven Brams, solved the problem of envy-free fair division for an arbitrary number of people with the Brams–Taylor procedure.Taylor received his Ph.D...
- Brams–Taylor procedureBrams–Taylor procedureThe Brams–Taylor theorem is a result in fair division discovered by Steven Brams and Alan D. Taylor. First published in the January 1995 issue of American Mathematical Monthly, it explicated the first finite procedure to produce an envy-free division of an infinitely divisible good among any...
- Equity (economics)Equity (economics)Equity is the concept or idea of fairness in economics, particularly as to taxation or welfare economics. More specifically it may refer to equal life chances regardless of identity, to provide all citizens with a basic minimum of income/goods/services or to increase funds and commitment for...
- Game theoryGame theoryGame theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
- Justice (economics)Justice (economics)Justice in economics is a subcategory of welfare economics with models frequently representing the ethical-social requirements of a given theory. That theory may or may not elicit acceptance...
- International tradeInternational tradeInternational trade is the exchange of capital, goods, and services across international borders or territories. In most countries, such trade represents a significant share of gross domestic product...
- Knapsack problemKnapsack problemThe knapsack problem or rucksack problem is a problem in combinatorial optimization: Given a set of items, each with a weight and a value, determine the count of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as...
- Nash bargaining game
- Pizza theoremPizza theoremIn elementary geometry, the pizza theorem states the equality of two areas that arise when one partitions a disk in a certain way.Let p be an interior point of the disk, and let n be a number that is evenly divisible by four and greater than or equal to eight...
- Sperner's lemmaSperner's lemmaIn mathematics, Sperner's lemma is a combinatorial analog of the Brouwer fixed point theorem, which follows from it. Sperner's lemma states that every Sperner coloring of a triangulation of an n-dimensional simplex contains a cell colored with a complete set of colors...
- SpiteSpiteIn fair division problems, spite is a phenomenon that occurs when a player's value of an allocation decreases when one or more other players' valuation increases...
- Steven BramsSteven BramsSteven J. Brams is a game theorist and political scientist at the New York University Department of Politics. Brams is best known for using the techniques of game theory and public choice to research voting systems and fair division. He is one of the independent discoverers of approval voting...
- Topological combinatoricsTopological combinatoricsThe discipline of combinatorial topology used combinatorial concepts in topology and in the early 20th century this gradually turned into the field of algebraic topology....
- Tragedy of the anticommonsTragedy of the anticommonsThe tragedy of the anticommons is a neologism coined by Michael Heller to describe a coordination breakdown where the existence of numerous rightsholders frustrates achieving a socially desirable outcome. The term mirrors the older term tragedy of the commons used to describe coordination...
- Tragedy of the commonsTragedy of the commonsThe tragedy of the commons is a dilemma arising from the situation in which multiple individuals, acting independently and rationally consulting their own self-interest, will ultimately deplete a shared limited resource, even when it is clear that it is not in anyone's long-term interest for this...
- Weakly additiveWeakly additiveIn fair division, a set of preferences is weakly additiveif the following condition is met:Weak additivity is often a realistic assumption when dividing up goods between claimants, and simplifies the mathematics of certain fair division problems considerably.-Use of weak additivity:Some procedures...
Further reading
- Steven J. Brams and Alan D. Taylor (1996). Fair Division - From cake-cutting to dispute resolution Cambridge University Press. ISBN 0-521-55390-3
- T.P. Hill (2000). "Mathematical devices for getting a fair share", American Scientist, Vol. 88, 325-331.
- Jack Robertson and William Webb (1998). Cake-Cutting Algorithms: Be Fair If You Can, AK Peters Ltd, . ISBN 1-56881-076-8.
External links
- Short essay about the cake-cutting problem by S. Abbas Raza of 3 Quarks Daily.
- Fair Division from the Discrete Mathematics Project at the University of Colorado at Boulder.
- The Fair Division Calculator (Java applet) at Harvey Mudd College
- Fair Division: Method of Lone Divider
- Fair Division: Method of Markers
- Fair Division: Method of Sealed Bids
- Vincent P. Crawford (1987). "fair division," The New Palgrave: A Dictionary of Economics, v. 2, pp. 274–75.
- Hal Varian (1987). "fairness," The New Palgrave: A Dictionary of Economics, v. 2, pp. 275–76.
- Bryan Skyrms (1996). The Evolution of the Social Contract Cambridge University Press. ISBN 9780521555838

