Fannes–Audenaert inequality
Encyclopedia
The Fannes–Audenaert inequality is a mathematical bound on the difference between the von Neumann entropies
of two density matrices
as a function of their trace distance
. It was proved by Koenraad M. R. Audenaert in 2007 as an optimal refinement of M. Fannes' original inequality, which was published in 1973.
and 
of dimensions 
,
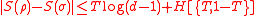
where
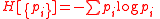
is the (Shannon) entropy of the probability distribution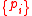
,
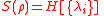
is the (von Neumann) entropy of a matrix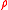
with eigenvalues 
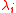, and
is the trace distance between the two matrices. Note that the base for the logarithm
is arbitrary, so long as the same base is used on both sides of the inequality.
Audenaert also proved that—given only the trace distance T and the dimension d—this is the optimal bound. He did this by directly exhibiting a pair of matrices which saturate the bound for any values of T and d. The matrices (which are diagonal in the same basis, i.e. they commute) are
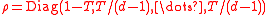
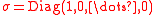
when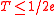
. He also proved the weaker inequality
which can be used for larger T.
Fannes proved this inequality as a means to prove the continuity
of the von Neumann entropy
, which did not require an optimal bound. The proof is very compact, and can be found in the textbook by Nielsen and Chuang. Audenaert's proof of the optimal inequality, on the other hand, is significantly more complicated.
Von Neumann entropy
In quantum statistical mechanics, von Neumann entropy, named after John von Neumann, is the extension of classical entropy concepts to the field of quantum mechanics....
of two density matrices
Density matrix
In quantum mechanics, a density matrix is a self-adjoint positive-semidefinite matrix of trace one, that describes the statistical state of a quantum system...
as a function of their trace distance
Trace distance
In quantum mechanics, and especially quantum information and the study of open quantum systems, the trace distance T is a metric on the space of density matrices...
. It was proved by Koenraad M. R. Audenaert in 2007 as an optimal refinement of M. Fannes' original inequality, which was published in 1973.
Statement of inequality
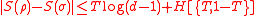
For any two density matrices and of dimensions ,where
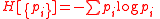
is the (Shannon) entropy of the probability distribution
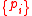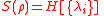
,is the (von Neumann) entropy of a matrix
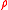with eigenvalues 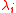, andis the trace distance between the two matrices. Note that the base for the logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
is arbitrary, so long as the same base is used on both sides of the inequality.
Audenaert also proved that—given only the trace distance T and the dimension d—this is the optimal bound. He did this by directly exhibiting a pair of matrices which saturate the bound for any values of T and d. The matrices (which are diagonal in the same basis, i.e. they commute) are
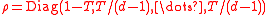
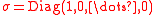
Fannes' inequality and Audenaert's refinement
The original inequality proved by Fannes waswhen
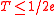. He also proved the weaker inequalitywhich can be used for larger T.
Fannes proved this inequality as a means to prove the continuity
Continuity
Continuity may refer to:In mathematics:* The opposing concept to discreteness; common examples include:** Continuous probability distribution or random variable in probability and statistics...
of the von Neumann entropy
Von Neumann entropy
In quantum statistical mechanics, von Neumann entropy, named after John von Neumann, is the extension of classical entropy concepts to the field of quantum mechanics....
, which did not require an optimal bound. The proof is very compact, and can be found in the textbook by Nielsen and Chuang. Audenaert's proof of the optimal inequality, on the other hand, is significantly more complicated.