Fast wavelet transform
Encyclopedia
The Fast Wavelet Transform is a mathematical
algorithm
designed to turn a waveform
or signal in the time domain
into a sequence
of coefficients based on an orthogonal basis
of small finite waves, or wavelets. The transform can be easily extended to multidimensional signals, such as images, where the time domain is replaced with the space domain.
It has as theoretical foundation the device of a finitely generated, orthogonal multiresolution analysis
(MRA). In the terms given there, one selects a sampling scale J with sampling rate
of 2J per unit interval, and projects the given signal f onto the space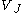 ; in theory by computing the scalar product
; in theory by computing the scalar product
s
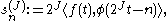
where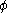 is the scaling function of the chosen wavelet transform; in practice by any suitable sampling procedure under the condition that the signal is highly oversampled, so
is the scaling function of the chosen wavelet transform; in practice by any suitable sampling procedure under the condition that the signal is highly oversampled, so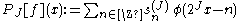
is the orthogonal projection or at least some good approximation of the original signal in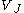 .
.
The MRA is characterised by its scaling sequence
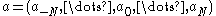 or, as Z-transform
or, as Z-transform
,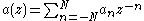
and its wavelet sequence
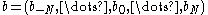 or
or 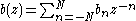
(some coefficients might be zero). Those allow to compute the wavelet coefficients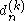 , at least some range k=M,...,J-1, without having to approximate the integrals in the corresponding scalar products. Instead, one can directly, with the help of convolution and decimation operators, compute those coefficients from the first approximation
, at least some range k=M,...,J-1, without having to approximate the integrals in the corresponding scalar products. Instead, one can directly, with the help of convolution and decimation operators, compute those coefficients from the first approximation 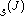 .
.
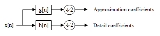
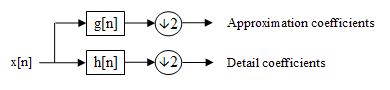
Forward DWT
One computes recursively
, starting with the coefficient sequence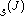 and counting down from k=J-1 down to some M
and counting down from k=J-1 down to some M,
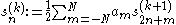 or
or 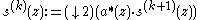
and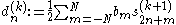 or
or 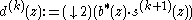 ,
,
for k=J-1,J-2,...,M and all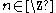 . In the Z-transform notation:
. In the Z-transform notation:
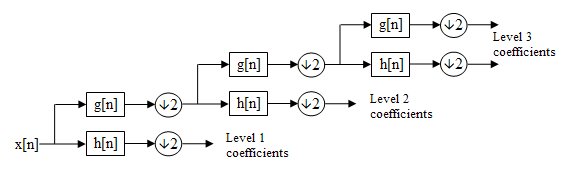
It follows that
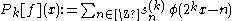
is the orthogonal projection of the original signal f or at least of the first approximation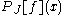 onto the subspace
onto the subspace
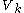 , that is, with sampling rate of 2k per unit interval. The difference to the first approximation is given by
, that is, with sampling rate of 2k per unit interval. The difference to the first approximation is given by
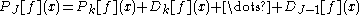 ,
,
where the difference or detail signals are computed from the detail coefficients as
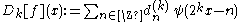 ,
,
with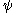 denoting the mother wavelet of the wavelet transform.
denoting the mother wavelet of the wavelet transform.
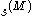 for some M
for some M and all the difference sequences 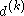 , k=M,...,J-1, one computes recursively
, k=M,...,J-1, one computes recursively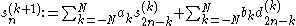 or
or 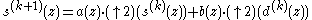
for k=J-1,J-2,...,M and all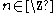 . In the Z-transform notation:
. In the Z-transform notation:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
designed to turn a waveform
Waveform
Waveform means the shape and form of a signal such as a wave moving in a physical medium or an abstract representation.In many cases the medium in which the wave is being propagated does not permit a direct visual image of the form. In these cases, the term 'waveform' refers to the shape of a graph...
or signal in the time domain
Time domain
Time domain is a term used to describe the analysis of mathematical functions, physical signals or time series of economic or environmental data, with respect to time. In the time domain, the signal or function's value is known for all real numbers, for the case of continuous time, or at various...
into a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of coefficients based on an orthogonal basis
Orthogonal basis
In mathematics, particularly linear algebra, an orthogonal basis for an inner product space is a basis for whose vectors are mutually orthogonal...
of small finite waves, or wavelets. The transform can be easily extended to multidimensional signals, such as images, where the time domain is replaced with the space domain.
It has as theoretical foundation the device of a finitely generated, orthogonal multiresolution analysis
Multiresolution analysis
A multiresolution analysis or multiscale approximation is the design method of most of the practically relevant discrete wavelet transforms and the justification for the algorithm of the fast wavelet transform...
(MRA). In the terms given there, one selects a sampling scale J with sampling rate
Sampling rate
The sampling rate, sample rate, or sampling frequency defines the number of samples per unit of time taken from a continuous signal to make a discrete signal. For time-domain signals, the unit for sampling rate is hertz , sometimes noted as Sa/s...
of 2J per unit interval, and projects the given signal f onto the space
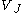 ; in theory by computing the scalar product
; in theory by computing the scalar productDot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
s
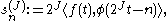
where
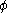 is the scaling function of the chosen wavelet transform; in practice by any suitable sampling procedure under the condition that the signal is highly oversampled, so
is the scaling function of the chosen wavelet transform; in practice by any suitable sampling procedure under the condition that the signal is highly oversampled, so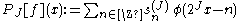
is the orthogonal projection or at least some good approximation of the original signal in
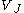 .
.The MRA is characterised by its scaling sequence
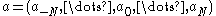 or, as Z-transform
or, as Z-transformZ-transform
In mathematics and signal processing, the Z-transform converts a discrete time-domain signal, which is a sequence of real or complex numbers, into a complex frequency-domain representation....
,
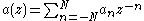
and its wavelet sequence
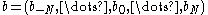 or
or 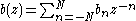
(some coefficients might be zero). Those allow to compute the wavelet coefficients
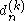 , at least some range k=M,...,J-1, without having to approximate the integrals in the corresponding scalar products. Instead, one can directly, with the help of convolution and decimation operators, compute those coefficients from the first approximation
, at least some range k=M,...,J-1, without having to approximate the integrals in the corresponding scalar products. Instead, one can directly, with the help of convolution and decimation operators, compute those coefficients from the first approximation 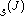 .
. Forward DWTDiscrete wavelet transformIn numerical analysis and functional analysis, a discrete wavelet transform is any wavelet transform for which the wavelets are discretely sampled...
One computes recursivelyRecursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
, starting with the coefficient sequence
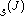 and counting down from k=J-1 down to some M
and counting down from k=J-1 down to some M
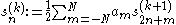 or
or 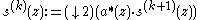
and
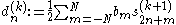 or
or 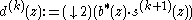 ,
,for k=J-1,J-2,...,M and all
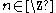 . In the Z-transform notation:
. In the Z-transform notation:
- The downsampling operatorDownsamplingIn signal processing, downsampling is the process of reducing the sampling rate of a signal. This is usually done to reduce the data rate or the size of the data....
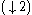 reduces an infinite sequence, given by its Z-transformZ-transformIn mathematics and signal processing, the Z-transform converts a discrete time-domain signal, which is a sequence of real or complex numbers, into a complex frequency-domain representation....
reduces an infinite sequence, given by its Z-transformZ-transformIn mathematics and signal processing, the Z-transform converts a discrete time-domain signal, which is a sequence of real or complex numbers, into a complex frequency-domain representation....
, which is simply a Laurent seriesLaurent seriesIn mathematics, the Laurent series of a complex function f is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where...
, to the sequence of the coefficients with even indices,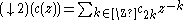 .
. - The starred Laurent-polynomial
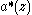 denotes the adjoint filter, it has time-reversed adjoint coefficients,
denotes the adjoint filter, it has time-reversed adjoint coefficients, 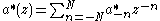 . (The adjoint of a real number being the number itself, of a complex number its conjugate, of a real matrix the transposed matrix, of a complex matrix its hermitian adjoint).
. (The adjoint of a real number being the number itself, of a complex number its conjugate, of a real matrix the transposed matrix, of a complex matrix its hermitian adjoint). - Multiplication is polynomial multiplication, which is equivalent to the convolution of the coefficient sequences.
It follows that
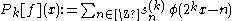
is the orthogonal projection of the original signal f or at least of the first approximation
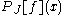 onto the subspace
onto the subspaceLinear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
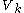 , that is, with sampling rate of 2k per unit interval. The difference to the first approximation is given by
, that is, with sampling rate of 2k per unit interval. The difference to the first approximation is given by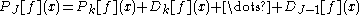 ,
,where the difference or detail signals are computed from the detail coefficients as
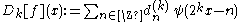 ,
,with
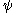 denoting the mother wavelet of the wavelet transform.
denoting the mother wavelet of the wavelet transform.Inverse DWT
Given the coefficient sequence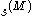 for some M
for some M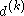 , k=M,...,J-1, one computes recursively
, k=M,...,J-1, one computes recursively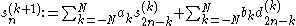 or
or 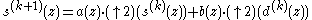
for k=J-1,J-2,...,M and all
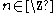 . In the Z-transform notation:
. In the Z-transform notation:
- The upsampling operatorUpsamplingUpsampling is the process of increasing the sampling rate of a signal. For instance, upsampling raster images such as photographs means increasing the resolution of the image....
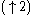 creates zero-filled holes inside a given sequence. That is, every second element of the resulting sequence is an element of the given sequence, every other second element is zero or
creates zero-filled holes inside a given sequence. That is, every second element of the resulting sequence is an element of the given sequence, every other second element is zero or 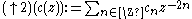 . This linear operator is, in the Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
. This linear operator is, in the Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
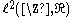 , the adjoint to the downsampling operator
, the adjoint to the downsampling operator 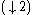 .
.

