
Discrete wavelet transform
Encyclopedia

Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
and functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, a discrete wavelet transform (DWT) is any wavelet transform for which the wavelet
Wavelet
A wavelet is a wave-like oscillation with an amplitude that starts out at zero, increases, and then decreases back to zero. It can typically be visualized as a "brief oscillation" like one might see recorded by a seismograph or heart monitor. Generally, wavelets are purposefully crafted to have...
s are discretely sampled. As with other wavelet transforms, a key advantage it has over Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
s is temporal resolution: it captures both frequency and location information (location in time).
Haar wavelets
The first DWT was invented by the Hungarian mathematician Alfréd HaarAlfréd Haar
Alfréd Haar was a Jewish Hungarian mathematician. In 1904 he began to study at the University of Göttingen. His doctorate was supervised by David Hilbert. The Haar measure, Haar wavelet, and Haar transform are named in his honor....
. For an input represented by a list of
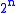 numbers, the Haar wavelet
numbers, the Haar waveletHaar wavelet
In mathematics, the Haar wavelet is a certain sequence of rescaled "square-shaped" functions which together form a wavelet family or basis. Wavelet analysis is similar to Fourier analysis in that it allows a target function over an interval to be represented in terms of an orthonormal function basis...
transform may be considered to simply pair up input values, storing the difference and passing the sum. This process is repeated recursively, pairing up the sums to provide the next scale: finally resulting in
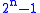 differences and one final sum.
differences and one final sum.Daubechies wavelets
The most commonly used set of discrete wavelet transforms was formulated by the Belgian mathematician Ingrid DaubechiesIngrid Daubechies
Ingrid Daubechies is a Belgian physicist and mathematician. She was between 2004 and 2011 the William R. Kenan Jr. Professor in the mathematics and applied mathematics departments at Princeton University. In January 2011 she moved to Duke University as a Professor in mathematics. She is the first...
in 1988. This formulation is based on the use of recurrence relation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
s to generate progressively finer discrete samplings of an implicit mother wavelet function; each resolution is twice that of the previous scale. In her seminal paper, Daubechies derives a family of wavelets
Daubechies wavelet
Named after Ingrid Daubechies, the Daubechies wavelets are a family of orthogonal wavelets defining a discrete wavelet transform and characterized by a maximal number of vanishing moments for some given support...
, the first of which is the Haar wavelet. Interest in this field has exploded since then, and many variations of Daubechies' original wavelets were developed.
Others
Other forms of discrete wavelet transform include the non- or undecimated wavelet transform (where downsampling is omitted), the Newland transform (where an orthonormal basis of wavelets is formed from appropriately constructed top-hat filterTop-hat filter
The Top-hat filter is several real-space or Fourier space filtering techniques. The name top-hat originates from the shape of the filter, which is a rectangle function, when viewed in the domain in which the filter is constructed.-Real space:...
s in frequency space). Wavelet packet transform
Wavelet packet decomposition
Wavelet packet decomposition is a wavelet transform where the signal is passed through more filters than the discrete wavelet transform ....
s are also related to the discrete wavelet transform. Complex wavelet transform
Complex wavelet transform
The complex wavelet transform is a complex-valued extension to the standard discrete wavelet transform . It is a two-dimensional wavelet transform which provides multiresolution, sparse representation, and useful characterization of the structure of an image. Further, it purveys a high degree of...
is another form.
Properties
The Haar DWT illustrates the desirable properties of wavelets in general. First, it can be performed in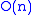 operations; second, it captures not only a notion of the frequency content of the input, by examining it at different scales, but also temporal content, i.e. the times at which these frequencies occur. Combined, these two properties make the Fast wavelet transform
operations; second, it captures not only a notion of the frequency content of the input, by examining it at different scales, but also temporal content, i.e. the times at which these frequencies occur. Combined, these two properties make the Fast wavelet transformFast wavelet transform
The Fast Wavelet Transform is a mathematical algorithm designed to turn a waveform or signal in the time domain into a sequence of coefficients based on an orthogonal basis of small finite waves, or wavelets...
(FWT) an alternative to the conventional Fast Fourier Transform
Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
(FFT).
Applications
The discrete wavelet transform has a huge number of applications in science, engineering, mathematics and computer science. Most notably, it is used for signal coding, to represent a discrete signal in a more redundant form, often as a preconditioning for data compressionData compression
In computer science and information theory, data compression, source coding or bit-rate reduction is the process of encoding information using fewer bits than the original representation would use....
. Practical applications can also be found in signal processing of accelerations for gait analysis.
Comparison with Fourier transform
To illustrate the differences and similarities between the discrete wavelet transform with the discrete Fourier transformDiscrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
, consider the DWT and DFT of the following sequence: (1,0,0,0), a unit impulse.
The DFT has orthogonal basis (DFT matrix
DFT matrix
A DFT matrix is an expression of a discrete Fourier transform as a matrix multiplication.-Definition:An N-point DFT is expressed as an N-by-N matrix multiplication as X = W x, where x is the original input signal, and X is the DFT of the signal.The transformation W of size N\times N can be defined...
):
1 1 1 1
1 0 –1 0
0 1 0 –1
1 –1 1 –1
while the DWT with Haar wavelets for length 4 data has orthogonal basis in the rows of:
1 1 1 1
1 1 –1 –1
1 –1 0 0
0 0 1 –1
(To simplify notation, whole numbers are used, so the bases are orthogonal but not orthonormal.)
Preliminary observations include:
- Wavelets have location – the (1,1,–1,–1) wavelet corresponds to “left side” versus “right side”, while the last two wavelets have support on the left side or the right side, and one is a translation of the other.
- Sinusoidal waves do not have location – they spread across the whole space – but do have phase – the second and third waves are translations of each other, corresponding to being 90° out of phase, like cosine and sine, of which these are discrete versions.
Decomposing the sequence with respect to these bases yields:
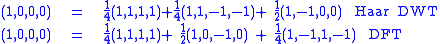
The DWT demonstrates the localization: the (1,1,1,1) term gives the average signal value, the (1,1,–1,–1) places the signal in the left side of the domain, and the
(1,–1,0,0) places it at the left side of the left side, and truncating at any stage yields a downsampled version of the signal:
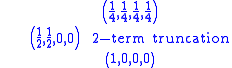
.svg.png)
Low-pass filter
A low-pass filter is an electronic filter that passes low-frequency signals but attenuates signals with frequencies higher than the cutoff frequency. The actual amount of attenuation for each frequency varies from filter to filter. It is sometimes called a high-cut filter, or treble cut filter...
ed version of the series:
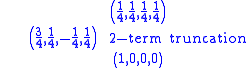
Notably, the middle approximation (2-term) differs. From the frequency domain perspective, this is a better approximation, but from the time domain perspective it has drawbacks – it exhibits undershoot – one of the values is negative, though the original series is non-negative everywhere – and ringing
Ringing (signal)
In electronics, signal processing, and video, ringing is unwanted oscillation of a signal, particularly in the step response...
, where the right side is non-zero, unlike in the wavelet transform. On the other hand, the Fourier approximation correctly shows a peak, and all points are within
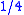 of their correct value, though all points have error. The wavelet approximation, by contrast, places a peak on the left half, but has no peak at the first point, and while it is exactly correct for half the values (reflecting location), it has an error of
of their correct value, though all points have error. The wavelet approximation, by contrast, places a peak on the left half, but has no peak at the first point, and while it is exactly correct for half the values (reflecting location), it has an error of 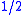 for the other values.
for the other values.This illustrates the kinds of trade-offs between these transforms, and how in some respects the DWT provides preferable behavior, particularly for the modeling of transients, which is of interest in applications.
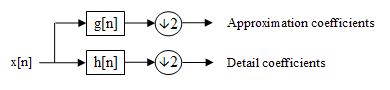
One level of the transform
The DWT of a signal is calculated by passing it through a series of filters. First the samples are passed through a low pass filter with impulse response
is calculated by passing it through a series of filters. First the samples are passed through a low pass filter with impulse responseImpulse response
In signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...
 resulting in a convolution
resulting in a convolutionConvolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
of the two:
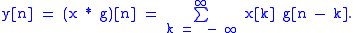
The signal is also decomposed simultaneously using a high-pass filter
High-pass filter
A high-pass filter is a device that passes high frequencies and attenuates frequencies lower than its cutoff frequency. A high-pass filter is usually modeled as a linear time-invariant system...
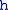 . The outputs giving the detail coefficients (from the high-pass filter) and approximation coefficients (from the low-pass). It is important that the two filters are related to each other and they are known as a quadrature mirror filter
. The outputs giving the detail coefficients (from the high-pass filter) and approximation coefficients (from the low-pass). It is important that the two filters are related to each other and they are known as a quadrature mirror filterQuadrature mirror filter
In digital signal processing, a quadrature mirror filter is a filter most commonly used to implement a filter bank that splits an input signal into two bands...
.
However, since half the frequencies of the signal have now been removed, half the samples can be discarded according to Nyquist’s rule. The filter outputs are then subsampled by 2 (Mallat's and the common notation is the opposite, g- high pass and h- low pass):
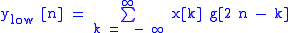
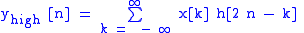
This decomposition has halved the time resolution since only half of each filter output characterises the signal. However, each output has half the frequency band of the input so the frequency resolution has been doubled.
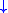
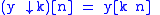
the above summation can be written more concisely.
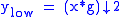
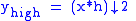
However computing a complete convolution
 with subsequent downsampling would waste computation time.
with subsequent downsampling would waste computation time.The Lifting scheme
Lifting scheme
The lifting scheme is a technique for both designing wavelets and performing the discrete wavelet transform.Actually it is worthwhile to merge these steps and design the wavelet filters while performing the wavelet transform....
is an optimization where these two computations are interleaved.
Cascading and Filter banks
This decomposition is repeated to further increase the frequency resolution and the approximation coefficients decomposed with high and low pass filters and then down-sampled. This is represented as a binary tree with nodes representing a sub-space with a different time-frequency localisation. The tree is known as a filter bankFilter bank
In signal processing, a filter bank is an array of band-pass filters that separates the input signal into multiple components, each one carrying a single frequency subband of the original signal. One application of a filter bank is a graphic equalizer, which can attenuate the components...
.
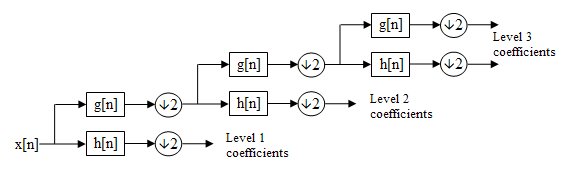
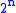 where
where  is the number of levels.
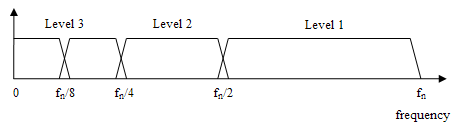
is the number of levels.For example a signal with 32 samples, frequency range 0 to
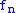 and 3 levels of decomposition, 4 output scales are produced:
and 3 levels of decomposition, 4 output scales are produced:| Level | Frequencies | Samples |
|---|---|---|
| 3 |  to to 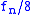 |
4 |
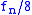 to to 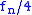 |
4 | |
| 2 | 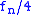 to to 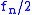 |
8 |
| 1 | 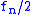 to to 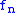 |
16 |
Other transforms
The Adam7 algorithmAdam7 algorithm
Adam7 is an interlacing algorithm for raster images, best known as the interlacing scheme optionally used in PNG images. An Adam7 interlaced image is broken into seven subimages, which are defined by replicating this 8×8 pattern across the full image....
, used for interlacing in the Portable Network Graphics (PNG) format, is a multiscale model of the data
which is similar to a DWT with Haar wavelet
Haar wavelet
In mathematics, the Haar wavelet is a certain sequence of rescaled "square-shaped" functions which together form a wavelet family or basis. Wavelet analysis is similar to Fourier analysis in that it allows a target function over an interval to be represented in terms of an orthonormal function basis...
s.
Unlike the DWT, it has a specific scale – it starts from an 8×8 block, and it downsamples the image, rather than decimating
Decimation (signal processing)
In digital signal processing, decimation is a technique for reducing the number of samples in a discrete-time signal. The element which implements this technique is referred to as a decimator.Decimation is a two-step process:...
(low-pass filter
Low-pass filter
A low-pass filter is an electronic filter that passes low-frequency signals but attenuates signals with frequencies higher than the cutoff frequency. The actual amount of attenuation for each frequency varies from filter to filter. It is sometimes called a high-cut filter, or treble cut filter...
ing, then downsampling). It thus offers worse frequency behavior, showing artifacts (pixelation
Pixelation
In computer graphics, pixelation is an effect caused by displaying a bitmap or a section of a bitmap at such a large size that individual pixels, small single-colored square display elements that comprise the bitmap, are visible to the eye...
) at the early stages, in return for simpler implementation.
Code examples
In its simplest form, the DWT is remarkably easy to compute.The Haar wavelet
Haar wavelet
In mathematics, the Haar wavelet is a certain sequence of rescaled "square-shaped" functions which together form a wavelet family or basis. Wavelet analysis is similar to Fourier analysis in that it allows a target function over an interval to be represented in terms of an orthonormal function basis...
in Java
Java (programming language)
Java is a programming language originally developed by James Gosling at Sun Microsystems and released in 1995 as a core component of Sun Microsystems' Java platform. The language derives much of its syntax from C and C++ but has a simpler object model and fewer low-level facilities...
:
public static int[] discreteHaarWaveletTransform(int[] input) {
// This function assumes that input.length=2^n, n>1
int[] output = new int[input.length];
for (int length = input.length >> 1; ; length >>= 1) {
// length = input.length / 2^n, WITH n INCREASING to log(input.length) / log(2)
for (int i = 0; i < length; ++i) {
int sum = input[i * 2] + input[i * 2 + 1];
int difference = input[i * 2] - input[i * 2 + 1];
output[i] = sum;
output[length + i] = difference;
}
if (length 1) {
return output;
}
//Swap arrays to do next iteration
System.arraycopy(output, 0, input, 0, length << 1);
}
}
Complete Java code for a 1-D and 2-D DWT using Haar
Haar wavelet
In mathematics, the Haar wavelet is a certain sequence of rescaled "square-shaped" functions which together form a wavelet family or basis. Wavelet analysis is similar to Fourier analysis in that it allows a target function over an interval to be represented in terms of an orthonormal function basis...
, Daubechies
Daubechies wavelet
Named after Ingrid Daubechies, the Daubechies wavelets are a family of orthogonal wavelets defining a discrete wavelet transform and characterized by a maximal number of vanishing moments for some given support...
, Coiflet
Coiflet
Coiflets are discrete wavelets designed by Ingrid Daubechies, at the request of Ronald Coifman, to have scaling functions with vanishing moments...
, and Legendre
Legendre wavelet
Compactly supported wavelets derived from Legendre polynomials are termed spherical harmonic or Legendre wavelets. Legendre functions have widespread applications in which spherical coordinate system are appropriate. As with many wavelets there is no nice analytical formula for describing these...
wavelets is available from the open source project: JWave.
Furthermore, a fast lifting implementation of the discrete biorthogonal CDF
Cohen-Daubechies-Feauveau wavelet
Cohen-Daubechies-Feauveau wavelet are the historically first family of biorthogonal wavelets, which was made popular by Ingrid Daubechies. These are not the same as the orthogonal Daubechies wavelets, and also not very similar in shape and properties...
9/7 wavelet transform in C
C (programming language)
C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....
, used in the JPEG 2000
JPEG 2000
JPEG 2000 is an image compression standard and coding system. It was created by the Joint Photographic Experts Group committee in 2000 with the intention of superseding their original discrete cosine transform-based JPEG standard with a newly designed, wavelet-based method...
image compression standard can be found here.

