Wavelet packet decomposition
Encyclopedia
Wavelet packet decomposition (WPD) (sometimes known as just wavelet packets) is a wavelet
transform where the signal is passed through more filters than the discrete wavelet transform
(DWT).
In the DWT, each level is calculated by passing only the previous approximation coefficients (cAj) through low and high pass quadrature mirror filter
s. However in the WPD, both the detail (cDj (in the 1-D case), cHj, cVj, cDj (in the 2-D case)) and approximation coefficients are decomposed to create the full binary tree.
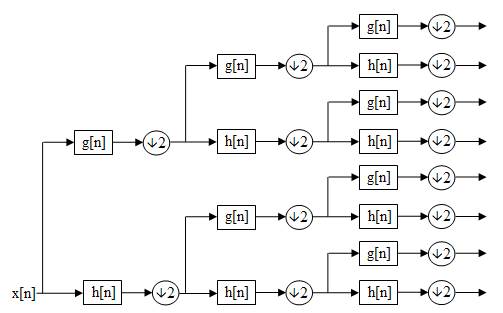For n levels of decomposition the WPD produces 2n different sets of coefficients (or nodes) as opposed to (3n + 1) sets for the DWT. However, due to the downsampling
process the overall number of coefficients is still the same and there is no redundancy.
From the point of view of compression, the standard wavelet transform may not produce the best result, since it is limited to wavelet bases that increase by a power of two towards the low frequencies. It could be that another combination of bases produce a more desirable representation for a particular signal. The best basis algorithm by Coifman and Wickerhauser finds a set of bases that provide the most desirable representation of the data relative to a particular cost function (e.g. entropy
).
Wavelet
A wavelet is a wave-like oscillation with an amplitude that starts out at zero, increases, and then decreases back to zero. It can typically be visualized as a "brief oscillation" like one might see recorded by a seismograph or heart monitor. Generally, wavelets are purposefully crafted to have...
transform where the signal is passed through more filters than the discrete wavelet transform
Discrete wavelet transform
In numerical analysis and functional analysis, a discrete wavelet transform is any wavelet transform for which the wavelets are discretely sampled...
(DWT).
In the DWT, each level is calculated by passing only the previous approximation coefficients (cAj) through low and high pass quadrature mirror filter
Quadrature mirror filter
In digital signal processing, a quadrature mirror filter is a filter most commonly used to implement a filter bank that splits an input signal into two bands...
s. However in the WPD, both the detail (cDj (in the 1-D case), cHj, cVj, cDj (in the 2-D case)) and approximation coefficients are decomposed to create the full binary tree.
Downsampling
In signal processing, downsampling is the process of reducing the sampling rate of a signal. This is usually done to reduce the data rate or the size of the data....
process the overall number of coefficients is still the same and there is no redundancy.
From the point of view of compression, the standard wavelet transform may not produce the best result, since it is limited to wavelet bases that increase by a power of two towards the low frequencies. It could be that another combination of bases produce a more desirable representation for a particular signal. The best basis algorithm by Coifman and Wickerhauser finds a set of bases that provide the most desirable representation of the data relative to a particular cost function (e.g. entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
).
External links
- An implementation of wavelet packet decomposition can be found in MATLAB wavelet toolbox: http://www.mathworks.com/access/helpdesk/help/toolbox/wavelet/index.html?/access/helpdesk/help/toolbox/wavelet/ch05_use.html.
- An illustration and implementation of wavelet packets along with its code in C++ can be found at http://www.bearcave.com/misl/misl_tech/wavelets/packet/index.html.
- JWave: An implementation in Java for 1-D and 2-D wavelet packets using HaarHaar waveletIn mathematics, the Haar wavelet is a certain sequence of rescaled "square-shaped" functions which together form a wavelet family or basis. Wavelet analysis is similar to Fourier analysis in that it allows a target function over an interval to be represented in terms of an orthonormal function basis...
, DaubechiesDaubechies waveletNamed after Ingrid Daubechies, the Daubechies wavelets are a family of orthogonal wavelets defining a discrete wavelet transform and characterized by a maximal number of vanishing moments for some given support...
, CoifletCoifletCoiflets are discrete wavelets designed by Ingrid Daubechies, at the request of Ronald Coifman, to have scaling functions with vanishing moments...
, and LegendreLegendre waveletCompactly supported wavelets derived from Legendre polynomials are termed spherical harmonic or Legendre wavelets. Legendre functions have widespread applications in which spherical coordinate system are appropriate. As with many wavelets there is no nice analytical formula for describing these...
wavelets.