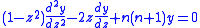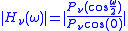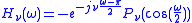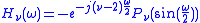
Legendre wavelet
Encyclopedia
Compactly supported wavelet
s derived from Legendre polynomials are termed spherical harmonic or Legendre wavelets. Legendre functions have widespread applications in which spherical coordinate system
are appropriate. As with many wavelets there is no nice analytical formula for describing these harmonic spherical wavelets. The low-pass filter associated to Legendre multiresolution analysis
is a finite impulse response
filter (FIR).
Wavelets associated to finite impulse response filters (FIR) are commonly preferred in most applications. An extra appealing feature is that the Legendre filters are linear phase FIR (i.e. multiresolution analysis associated with linear phase
filters). These wavelets have been implemented on MATLAB (wavelet toolbox). Although being compactly supported wavelet, legdN are not orthogonal (but for N = 1).
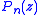are solutions of the Legendre 
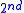-order differential equation, n integer:
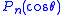polynomials can be used to define the smoothing filter 
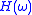of a multiresolution analysis (MRA). Since the appropriate boundary conditions for an MRA are 
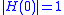and 
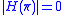, the smoothing filter of an MRA can be defined so that the magnitude of the low-pass 
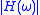can be associated to Legendre polynomials according to: 
.
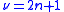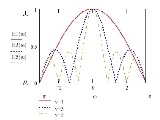
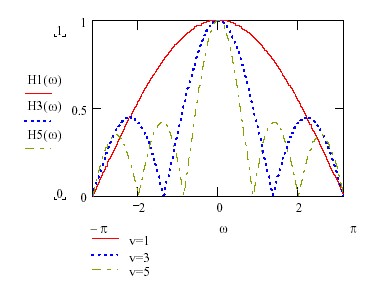
Illustrative examples of filter transfer functions for a Legendre MRA are shown in figure 1, for
=1,3 and 5. A low-pass behaviour is exhibited for the filter H, as expected. The number of zeroes within 
is equal to the degree of the Legendre polynomial. Therefore, the roll-off
of side-lobes with frequency is easily controlled by the parameter
.
The low-pass filter transfer function is given by
The transfer function of the high-pass analysing filter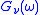
is chosen according to Quadrature mirror filter
condition, yielding:
Indee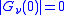d,
and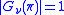 
, as expected.
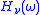to the form
The filter coefficients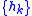
, 
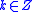are given by:
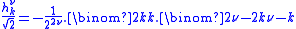
It follows then the symmetry: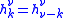
. There are just 
non-zero filter coefficients on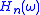 
, so that the Legendre wavelets have compact support for every odd integer 
.
wavelet toolbox -- The m-files to allow the computation of Legendre wavelet transform, details and filter are (freeware) available.
The finite support width Legendre family is denoted by legd (short name). Wavelets: 'legdN'. The parameter N in the legdN family is found according to 2N=
+1 (length of the MRA filters).
Legendre wavelets can be derived from the low-pass reconstruction filter by an iterative procedure (the cascade algorithm
). The wavelet has compact support and finite impulse response AMR filters (FIR) are used (table 1). The first wavelet of the Legendre's family is exactly the well-known Haar wavelet
. Figure 2 shows an emerging pattern that progressively looks like the wavelet's shape.
The Legendre wavelet shape can be visualised using the wavemenu command of MATLAB. Figure 3 shows legd8 wavelet displayed using MATLABTM. Legendre Polynomials are also associated with windows families.
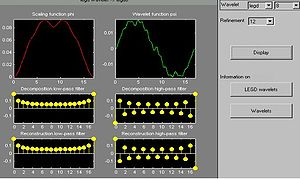
Wavelet
A wavelet is a wave-like oscillation with an amplitude that starts out at zero, increases, and then decreases back to zero. It can typically be visualized as a "brief oscillation" like one might see recorded by a seismograph or heart monitor. Generally, wavelets are purposefully crafted to have...
s derived from Legendre polynomials are termed spherical harmonic or Legendre wavelets. Legendre functions have widespread applications in which spherical coordinate system
Spherical coordinate system
In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its inclination angle measured from a fixed zenith direction, and the azimuth angle of...
are appropriate. As with many wavelets there is no nice analytical formula for describing these harmonic spherical wavelets. The low-pass filter associated to Legendre multiresolution analysis
Multiresolution analysis
A multiresolution analysis or multiscale approximation is the design method of most of the practically relevant discrete wavelet transforms and the justification for the algorithm of the fast wavelet transform...
is a finite impulse response
Finite impulse response
A finite impulse response filter is a type of a signal processing filter whose impulse response is of finite duration, because it settles to zero in finite time. This is in contrast to infinite impulse response filters, which have internal feedback and may continue to respond indefinitely...
filter (FIR).
Wavelets associated to finite impulse response filters (FIR) are commonly preferred in most applications. An extra appealing feature is that the Legendre filters are linear phase FIR (i.e. multiresolution analysis associated with linear phase
Linear phase
Linear phase is a property of a filter, where the phase response of the filter is a linear function of frequency, excluding the possibility of wraps at \pm\pi. In a causal system, perfect linear phase can be achieved with a discrete-time FIR filter...
filters). These wavelets have been implemented on MATLAB (wavelet toolbox). Although being compactly supported wavelet, legdN are not orthogonal (but for N = 1).
Legendre multiresolution filters
Associated Legendre polynomials are the colatitudinal part of the spherical harmonics which are common to all separations of Laplace's equation in spherical polar coordinates. The radial part of the solution varies from one potential to another, but the harmonics are always the same and are a consequence of spherical symmetry. Spherical harmonics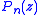 are solutions of the Legendre 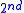-order differential equation, n integer:
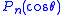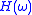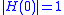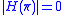polynomials can be used to define the smoothing filter of a multiresolution analysis (MRA). Since the appropriate boundary conditions for an MRA are and , the smoothing filter of an MRA can be defined so that the magnitude of the low-pass 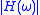can be associated to Legendre polynomials according to: .
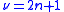Illustrative examples of filter transfer functions for a Legendre MRA are shown in figure 1, for
=1,3 and 5. A low-pass behaviour is exhibited for the filter H, as expected. The number of zeroes within is equal to the degree of the Legendre polynomial. Therefore, the roll-offRoll-off
Roll-off is a term commonly used to describe the steepness of a transmission function with frequency, particularly in electrical network analysis, and most especially in connection with filter circuits in the transition between a passband and a stopband...
of side-lobes with frequency is easily controlled by the parameter
.
The transfer function of the high-pass analysing filter
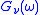is chosen according to Quadrature mirror filterQuadrature mirror filter
In digital signal processing, a quadrature mirror filter is a filter most commonly used to implement a filter bank that splits an input signal into two bands...
condition, yielding:
Indeed,
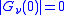and 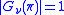, as expected.Legendre multiresolution filter coefficients
A suitable phase assignment is done so as to properly adjust the transfer function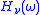 to the formThe filter coefficients
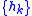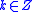, are given by: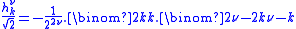It follows then the symmetry:
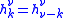. There are just non-zero filter coefficients on 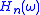, so that the Legendre wavelets have compact support for every odd integer .-
-
- Table I - Smoothing Legendre FIR filter coefficients for
=1,3,5 (N is the wavelet order.)
(N=1)
(N=2)
(N=3)
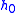
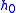
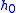
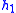
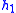
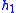
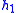
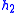
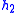
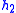
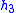
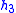
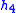
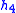
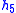
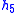
- N.B. The minus signal can be suppressed.
- Table I - Smoothing Legendre FIR filter coefficients for
-
MATLAB implementation of Legendre wavelets
Legendre wavelets can be easily loaded into the MATLABMATLAB
MATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...
wavelet toolbox -- The m-files to allow the computation of Legendre wavelet transform, details and filter are (freeware) available.
The finite support width Legendre family is denoted by legd (short name). Wavelets: 'legdN'. The parameter N in the legdN family is found according to 2N=
+1 (length of the MRA filters).Legendre wavelets can be derived from the low-pass reconstruction filter by an iterative procedure (the cascade algorithm
Cascade algorithm
In the mathematical topic of wavelet theory, the cascade algorithm is a numerical method for calculating function values of the basic scaling and wavelet functions of a discrete wavelet transform using an iterative algorithm. It starts from values on a coarse sequence of sampling points and...
). The wavelet has compact support and finite impulse response AMR filters (FIR) are used (table 1). The first wavelet of the Legendre's family is exactly the well-known Haar wavelet
Haar wavelet
In mathematics, the Haar wavelet is a certain sequence of rescaled "square-shaped" functions which together form a wavelet family or basis. Wavelet analysis is similar to Fourier analysis in that it allows a target function over an interval to be represented in terms of an orthonormal function basis...
. Figure 2 shows an emerging pattern that progressively looks like the wavelet's shape.
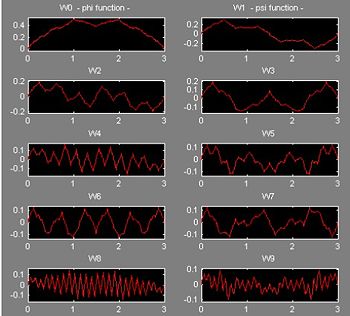
Legendre wavelet packets
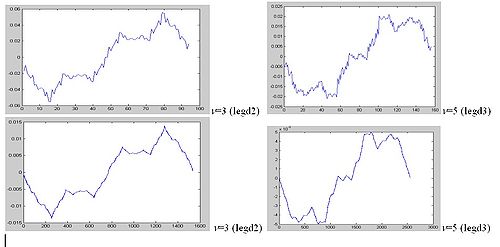
Wavelet packets (WP) systems derived from Legendre wavelets can also be easily accomplished. Figure 5 illustrates the WP functions derived from legd2.