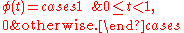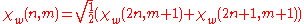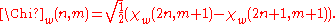Haar wavelet
Encyclopedia
In mathematics, the Haar wavelet is a certain sequence of rescaled "square-shaped" functions which together form a wavelet family or basis. Wavelet analysis is similar to Fourier analysis in that it allows a target function over an interval to be represented in terms of an orthonormal function basis. The Haar sequence is now recognised as the first known wavelet
basis and extensively used as a teaching example in the theory of wavelets.
The Haar sequence was proposed in 1909 by Alfréd Haar
. Haar used these functions to give an example of a countable orthonormal system for the space of square-integrable function
s on the real line
. The study of wavelets, and even the term "wavelet", did not come until much later. As a special case of the Daubechies wavelet
, it is also known as D2.
The Haar wavelet is also the simplest possible wavelet. The technical disadvantage of the Haar wavelet is that it is not continuous
, and therefore not differentiable
. This property can, however, be an advantage for the analysis of signals with sudden transitions, such as monitoring of tool failure in machines.
The Haar wavelet's mother wavelet function 
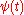can be described as
Wavelet
A wavelet is a wave-like oscillation with an amplitude that starts out at zero, increases, and then decreases back to zero. It can typically be visualized as a "brief oscillation" like one might see recorded by a seismograph or heart monitor. Generally, wavelets are purposefully crafted to have...
basis and extensively used as a teaching example in the theory of wavelets.
The Haar sequence was proposed in 1909 by Alfréd Haar
Alfréd Haar
Alfréd Haar was a Jewish Hungarian mathematician. In 1904 he began to study at the University of Göttingen. His doctorate was supervised by David Hilbert. The Haar measure, Haar wavelet, and Haar transform are named in his honor....
. Haar used these functions to give an example of a countable orthonormal system for the space of square-integrable function
Square-integrable function
In mathematics, a quadratically integrable function, also called a square-integrable function, is a real- or complex-valued measurable function for which the integral of the square of the absolute value is finite...
s on the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
. The study of wavelets, and even the term "wavelet", did not come until much later. As a special case of the Daubechies wavelet
Daubechies wavelet
Named after Ingrid Daubechies, the Daubechies wavelets are a family of orthogonal wavelets defining a discrete wavelet transform and characterized by a maximal number of vanishing moments for some given support...
, it is also known as D2.
The Haar wavelet is also the simplest possible wavelet. The technical disadvantage of the Haar wavelet is that it is not continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
, and therefore not differentiable
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
. This property can, however, be an advantage for the analysis of signals with sudden transitions, such as monitoring of tool failure in machines.
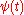can be described as
-
Its scaling function
can be described as
Haar system
In functional analysisFunctional analysisFunctional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, the Haar systems denotes the set of Haar wavelets
In Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
terms, this constitutes a complete orthogonal system for the functions on the unit intervalUnit intervalIn mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
. There is a related Rademacher system (named after Hans RademacherHans RademacherHans Adolph Rademacher was a German mathematician, known for work in mathematical analysis and number theory.-Biography:...
) of sums of Haar functions, which is an orthogonal system but not complete.
The Haar system (with the natural ordering) is further a Schauder basisSchauder basisIn mathematics, a Schauder basis or countable basis is similar to the usual basis of a vector space; the difference is that Hamel bases use linear combinations that are finite sums, while for Schauder bases they may be infinite sums...
for the space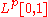
for 
. This basis is unconditional for p > 1.
Haar wavelet properties
The Haar wavelet has several notable properties:
- Any continuous real function can be approximated by linear combinationLinear combinationIn mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
s of
and their shifted functions. This extends to those function spaces where any function therein can be approximated by continuous functions. - Any continuous real function can be approximated by linear combinations of the constant function,
and their shifted functions. - OrthogonalityOrthogonalityOrthogonality occurs when two things can vary independently, they are uncorrelated, or they are perpendicular.-Mathematics:In mathematics, two vectors are orthogonal if they are perpendicular, i.e., they form a right angle...
in the form
-
- Here δi,j represents the Kronecker delta. The dual function of
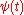is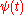 
itself.
- 4. Wavelet/scaling functions with different scale m have a functional relationship:
- 5. Coefficients of scale m can be calculated by coefficients of scale m+1:
- If
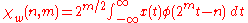
- and
- then
Haar matrix
The 2×2 Haar matrix that is associated with the Haar wavelet is
Using the discrete wavelet transformDiscrete wavelet transformIn numerical analysis and functional analysis, a discrete wavelet transform is any wavelet transform for which the wavelets are discretely sampled...
, one can transform any sequence
of even length into a sequence of two-component-vectors 
. If one right-multiplies each vector with the matrix 
, one gets the result 
of one stage of the fast Haar-wavelet transform. Usually one separates the sequences s and d and continues with transforming the sequence s.
If one has a sequence of length a multiple of four, one can build blocks of 4 elements and transform them in a similar manner with the 4×4 Haar matrix
which combines two stages of the fast Haar-wavelet transform.
Compare with a Walsh matrixWalsh matrixIn mathematics, a Walsh matrix is a specific square matrix, with dimensions a power of 2, the entries of which are +1 or −1, and the property that the dot product of any two distinct rows is zero. The Walsh matrix was proposed by Joseph Leonard Walsh in 1923...
, which is a non-localized 1/–1 matrix.
Haar transform
The Haar transform is the simplest of the wavelet transforms. This transform cross-multiplies a function against the Haar wavelet with various shifts and stretches, like the Fourier transform cross-multiplies a function against a sine wave with two phases and many stretches.
The Haar transform is derived from the Haar matrix. An example of a 4x4 Haar transformation matrix is shown below.
The Haar transform can be thought of as a sampling process in which rows of the transformation matrix act as samples of finer and finer resolution.
Compare with the Walsh transform, which is also 1/–1, but is non-localized.
External links
- Free Haar wavelet filtering implementation and interactive demo
- Free Haar wavelet denoising and lossy signal compression
Haar transform
- http://cnx.org/content/m11087/latest/
- http://math.hws.edu/eck/math371/applets/Haar.html
- http://online.redwoods.cc.ca.us/instruct/darnold/LAPROJ/Fall2002/ames/paper.pdf
- http://scien.stanford.edu/class/ee368/projects2000/project12/2.html
-
