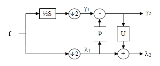
Lifting scheme
Encyclopedia
The lifting scheme is a technique for both designing wavelet
s and performing the discrete wavelet transform
.
Actually it is worthwhile to merge these steps and design the wavelet filters while performing the wavelet transform.
This is then called the second generation wavelet transform
.
The technique was introduced by Wim Sweldens.
The discrete wavelet transform applies several filters separately to the same signal.
In contrast to that, for the lifting scheme the signal is divided like a zipper.
Then a series of convolution-accumulate
operations across the divided signals is applied.
If a pair of filters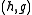 is complementary,
is complementary,
that is it allows for perfect reconstruction,
then for every filter
the pair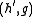 with
with 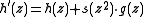 allows for perfect reconstruction, too.
allows for perfect reconstruction, too.
Of course, this is also true for every pair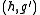 of the form
of the form 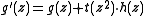 .
.
The converse is also true:
If the filterbanks and
and 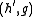 allow for perfect reconstruction,
allow for perfect reconstruction,
then there is a unique filter with
with 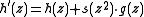 .
.
Each such transform of the filterbank (or the respective operation in a wavelet transform) is called a lifting step.
A sequence of lifting steps consists of alternating lifts,
that is, once the lowpass is fixed and the highpass is changed and in the next step the highpass is fixed and the lowpass is changed.
Successive steps of the same direction can be merged.
Although every reconstructable filter bank can be expressed in terms of lifting steps,
a general description of the lifting steps is not obvious from a description of a wavelet family.
However, for instance for simple cases of the Cohen-Daubechies-Feauveau wavelet
,
there is an explicit formula for their lifting steps.
(See the respective article)
is a derivative of the Lifting Scheme, in which the addition and subtraction operations are absorbed into the update and prediction steps, respectively. These steps can be any (invertible) mapping, leading to a more general lifting scheme.
Wavelet
A wavelet is a wave-like oscillation with an amplitude that starts out at zero, increases, and then decreases back to zero. It can typically be visualized as a "brief oscillation" like one might see recorded by a seismograph or heart monitor. Generally, wavelets are purposefully crafted to have...
s and performing the discrete wavelet transform
Discrete wavelet transform
In numerical analysis and functional analysis, a discrete wavelet transform is any wavelet transform for which the wavelets are discretely sampled...
.
Actually it is worthwhile to merge these steps and design the wavelet filters while performing the wavelet transform.
This is then called the second generation wavelet transform
Second generation wavelet transform
In signal processing, the second generation wavelet transform is a wavelet transform where the filters are not designed explicitly, but the transform consists of the application of the Lifting scheme....
.
The technique was introduced by Wim Sweldens.
The discrete wavelet transform applies several filters separately to the same signal.
In contrast to that, for the lifting scheme the signal is divided like a zipper.
Then a series of convolution-accumulate
Multiply-accumulate
In computing, especially digital signal processing, the multiply–accumulate operation is a common step that computes the product of two numbers and adds that product to an accumulator. The hardware unit that performs the operation is known as a multiplier–accumulator ; the operation itself is also...
operations across the divided signals is applied.
Basics
The basic idea of lifting is the following:If a pair of filters
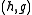 is complementary,
is complementary,that is it allows for perfect reconstruction,
then for every filter

the pair
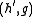 with
with 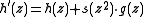 allows for perfect reconstruction, too.
allows for perfect reconstruction, too.Of course, this is also true for every pair
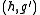 of the form
of the form 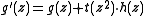 .
.The converse is also true:
If the filterbanks
 and
and 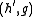 allow for perfect reconstruction,
allow for perfect reconstruction,then there is a unique filter
 with
with 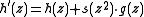 .
.Each such transform of the filterbank (or the respective operation in a wavelet transform) is called a lifting step.
A sequence of lifting steps consists of alternating lifts,
that is, once the lowpass is fixed and the highpass is changed and in the next step the highpass is fixed and the lowpass is changed.
Successive steps of the same direction can be merged.
Properties
- Perfect reconstruction
- Every transform by the lifting scheme can be inverted.
- Every perfect reconstruction filter bank can be decomposed into lifting steps by the Euclidean algorithmEuclidean algorithmIn mathematics, the Euclidean algorithm is an efficient method for computing the greatest common divisor of two integers, also known as the greatest common factor or highest common factor...
. - That is, "lifting decomposable filter bank" and "perfect reconstruction filter bank" denotes the same.
- Every two perfect reconstructable filter banks can be transformed into each other by a sequence of lifting steps. (If
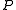 and
and  are polyphase matricesPolyphase matrixIn signal processing,a polyphase matrix is a matrix whose elements are filter masks.It represents a filter bank as it is usedin sub-band coders alias discrete wavelet transforms.If h,g are two filters,then one level the traditional wavelet transform...
are polyphase matricesPolyphase matrixIn signal processing,a polyphase matrix is a matrix whose elements are filter masks.It represents a filter bank as it is usedin sub-band coders alias discrete wavelet transforms.If h,g are two filters,then one level the traditional wavelet transform...
with the same determinant, the lifting sequence from to
to 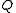 , is the same as the one from the lazy polyphase matrix
, is the same as the one from the lazy polyphase matrix 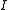 to
to 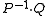 .)
.) - Speedup by a factor of two. This is only possible because lifting is restricted to perfect reconstruction filterbanks. That is, lifting somehow squeezes out redundancies caused by perfect reconstructability.
- In place: The transformation can be performed immediately in the memory of the input data with only constant memory overhead.
- Non-linearities: The convolution operations can be replaced by any other operation. For perfect reconstruction only the invertibility of the addition operation is relevant. This way rounding errors in convolution can be tolerated and bit-exact reconstruction is possible. However the numeric stability may be reduced by the non-linearities. This must be respected if the transformed signal is processed like in lossy compression.
Although every reconstructable filter bank can be expressed in terms of lifting steps,
a general description of the lifting steps is not obvious from a description of a wavelet family.
However, for instance for simple cases of the Cohen-Daubechies-Feauveau wavelet
Cohen-Daubechies-Feauveau wavelet
Cohen-Daubechies-Feauveau wavelet are the historically first family of biorthogonal wavelets, which was made popular by Ingrid Daubechies. These are not the same as the orthogonal Daubechies wavelets, and also not very similar in shape and properties...
,
there is an explicit formula for their lifting steps.
(See the respective article)
Generalized Lifting
The Generalized Lifting SchemeGeneralized Lifting
Generalized lifting scheme was developed by and and published in Joel's PhD Thesis. It is based on classical lifting scheme and generalizes it breaking out a restriction hidden in the scheme structure...
is a derivative of the Lifting Scheme, in which the addition and subtraction operations are absorbed into the update and prediction steps, respectively. These steps can be any (invertible) mapping, leading to a more general lifting scheme.
Applications
- Wavelet transform with integer values: WAILI
- Fourier transform with bit-exact reconstruction: Soontorn Oraintara, Ying-Jui Chen, Truong Q. Nguyen: Integer Fast Fourier Transform
- Construction of wavelets with a required number of smoothness factors and vanishing moments
- Construction of wavelets matched to a given pattern: Henning Thielemann: Optimally matched wavelets
- Implementation of the Discrete Wavelet TransformDiscrete wavelet transformIn numerical analysis and functional analysis, a discrete wavelet transform is any wavelet transform for which the wavelets are discretely sampled...
in JPEG 2000JPEG 2000JPEG 2000 is an image compression standard and coding system. It was created by the Joint Photographic Experts Group committee in 2000 with the intention of superseding their original discrete cosine transform-based JPEG standard with a newly designed, wavelet-based method...
See also
- The Feistel scheme in cryptology uses much the same idea of dividing data and alternating function application with addition. Both in the Feistel scheme and the Lifting scheme this is used for symmetric en- and decoding.
External links
- A comprehensive introduction to the Fast Lifting Wavelet Transform
- Ingrid Daubechies, Wim Sweldens: Factoring Wavelet Transforms into Lifting Steps
- Lifting wavelet Transform steps : http://www.mathnet.or.kr/Video/etc/dongseo/1002_Yoo.ppt
- The Lifting Scheme: A Construction of Second Generation Wavelets

