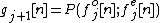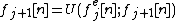Generalized Lifting
Encyclopedia
Generalized lifting scheme was developed by Joel Solé and Philippe Salembier and published in Joel's PhD Thesis. It is based on classical lifting scheme
and generalizes it breaking out a restriction hidden in the scheme structure. Classical lifting scheme has three kind of operations.
The scheme is invertible due to the structure of itself. In the receiver
the update step is computed first. Its result is added to the even samples. After that, it's possible to compute exactly the same prediction and add it to the odd samples. In order to recover the original signal, we have to invert the Lazy Wavelet Transform. Generalized lifting scheme has the same three kind of operations. However this scheme avoids the addition-subtraction restriction that offered Classical Lifting. That fact has some consequences. For example, the design of all steps must guarantee the scheme invertibility (not guaranteed if the addition-subtraction restriction is avoided).
Obviously, these mapping cannot be any function. In order the guarantee the invertibility of the scheme itself, all mapping involved in the transform, must be invertible. In case that mappings arise and arrive on finite sets (discrete bounded value signals), this condition is equivalent to say that mappings are injective
(one-to-one). Moreover, if mapping goes from one set to a set of the same cardinality, it should be bijective
.
In the Generalized Lifting Scheme the addition/subtraction restriction is avoided by including this step in the mapping. In this way the Classical Lifting Scheme is generalized.
Lifting scheme
The lifting scheme is a technique for both designing wavelets and performing the discrete wavelet transform.Actually it is worthwhile to merge these steps and design the wavelet filters while performing the wavelet transform....
and generalizes it breaking out a restriction hidden in the scheme structure. Classical lifting scheme has three kind of operations.
- Lazy wavelet transform splits signal
in two new signals: the odd samples signal denoted by 
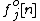and the even samples signal denoted by 
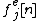. - Prediction step its objective is compute a prediction for the odd samples, based on the even samples (or viceversa). This prediction is subtracted to the odd samples creating an error signal
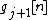. - Update step This step recalibrates the low frequency branch with some of the energy removed during subsampling. In the case of classical Lifting, this is used in order to "prepare" the signal for the next prediction step. It uses the predicted odd samples
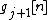to prepare the even ones 
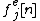(or viceversa). This update is subtracted to even samples producing the signal denoted by 
.
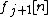The scheme is invertible due to the structure of itself. In the receiver
Receiver (Information Theory)
The receiver in information theory is the receiving end of a communication channel. It receives decoded messages/information from the sender, who first encoded them. Sometimes the receiver is modeled so as to include the decoder. Real-world receivers like radio receivers or telephones can not be...
the update step is computed first. Its result is added to the even samples. After that, it's possible to compute exactly the same prediction and add it to the odd samples. In order to recover the original signal, we have to invert the Lazy Wavelet Transform. Generalized lifting scheme has the same three kind of operations. However this scheme avoids the addition-subtraction restriction that offered Classical Lifting. That fact has some consequences. For example, the design of all steps must guarantee the scheme invertibility (not guaranteed if the addition-subtraction restriction is avoided).
Definition
Generalized lifting scheme is a dyadic transform that follows the next rules:- Computes a Lazy Wavelet Transform and splits even samples from odd samples.
- Computes a Prediction MappingMap (mathematics)In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
. This step tries to predict odd samples taking into account the even ones (or viceversa). This a mapping from the space of the samples in
to the space of the samples in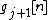 
. In this case the samples (from 
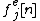) chosen to be the reference for 
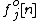are called the context. It could be expressed as:
- Computes an Update Mapping. This step tries to update the even samples taking into account the odd predicted samples. It would be a kind of preparation for the next prediction step, if any. It could be expressed:
Obviously, these mapping cannot be any function. In order the guarantee the invertibility of the scheme itself, all mapping involved in the transform, must be invertible. In case that mappings arise and arrive on finite sets (discrete bounded value signals), this condition is equivalent to say that mappings are injective
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
(one-to-one). Moreover, if mapping goes from one set to a set of the same cardinality, it should be bijective
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
.
In the Generalized Lifting Scheme the addition/subtraction restriction is avoided by including this step in the mapping. In this way the Classical Lifting Scheme is generalized.