
Fermat quotient
Encyclopedia
In number theory
, the Fermat quotient of an integer a ≥ 2 with respect to a prime
base p is defined as:
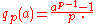
If a is coprime
to p then Fermat's little theorem
says that qp(a) will be an integer. The quotient is named after Pierre de Fermat
.
proved that if a and b are both coprime to p, then:

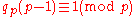

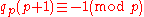
s. In general they are called Wieferich primes base a. Known solutions of qp(a) ≡ 0 (mod p) for small prime values of a are:
The smallest solutions of qp(a) ≡ 0 (mod p) with a = the nth prime are"
A pair (p,r) of prime numbers such that qp(r) ≡ 0 (mod p) and qr(p) ≡ 0 (mod r) is called a Wieferich pair
.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the Fermat quotient of an integer a ≥ 2 with respect to a prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
base p is defined as:
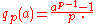
If a is coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
to p then Fermat's little theorem
Fermat's little theorem
Fermat's little theorem states that if p is a prime number, then for any integer a, a p − a will be evenly divisible by p...
says that qp(a) will be an integer. The quotient is named after Pierre de Fermat
Pierre de Fermat
Pierre de Fermat was a French lawyer at the Parlement of Toulouse, France, and an amateur mathematician who is given credit for early developments that led to infinitesimal calculus, including his adequality...
.
Properties
In 1850 Ferdinand EisensteinFerdinand Eisenstein
Ferdinand Gotthold Max Eisenstein was a German mathematician. He specialized in number theory and analysis, and proved several results that eluded even Gauss. Like Galois and Abel before him, Eisenstein died before the age of 30. He was born and died in Berlin, Germany.-Early life:He was born...
proved that if a and b are both coprime to p, then:

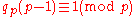

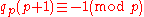
Generalized Wieferich primes
If qp(a) ≡ 0 (mod p) then ap-1 ≡ 1 (mod p2). Primes for which this is true for a = 2 are called Wieferich primeWieferich prime
In number theory, a Wieferich prime is a prime number p such that p2 divides 2p − 1 − 1, therefore connecting these primes with Fermat's little theorem, which states that every odd prime p divides 2p − 1 − 1...
s. In general they are called Wieferich primes base a. Known solutions of qp(a) ≡ 0 (mod p) for small prime values of a are:
| a | p | OEIS sequence |
|---|---|---|
| 2 | 1093, 3511 | |
| 3 | 11, 1006003 | |
| 5 | 2, 20771, 40487, 53471161, 1645333507, 6692367337, 188748146801 | |
| 7 | 5, 491531 | |
| 11 | 71 | |
| 13 | 2, 863, 1747591 | |
| 17 | 2, 3, 46021, 48947, 478225523351 | |
| 19 | 3, 7, 13, 43, 137, 63061489 | |
| 23 | 13, 2481757, 13703077, 15546404183, 2549536629329 |
The smallest solutions of qp(a) ≡ 0 (mod p) with a = the nth prime are"
- 1093, 11, 2, 5, 71, 2, 2, 3, 13, 2, 7, 2, 2, 5, … .
A pair (p,r) of prime numbers such that qp(r) ≡ 0 (mod p) and qr(p) ≡ 0 (mod r) is called a Wieferich pair
Wieferich pair
In mathematics, a Wieferich pair is a pair of prime numbers p and q that satisfyWieferich pairs are named after German mathematician Arthur Wieferich.There are only six Wieferich pairs known:...
.
External links
- Gottfried Helms. Fermat-/Euler-quotients (ap-1 – 1)/pk with arbitrary k.

