Wieferich prime
Encyclopedia
In number theory
, a Wieferich prime is a prime number
p such that p2 divides 2p − 1 − 1, therefore connecting these primes with Fermat's little theorem
, which states that every odd prime p divides 2p − 1 − 1. Wieferich primes were first described by Arthur Wieferich
in 1909 in works pertaining to Fermat's last theorem
, at which time both theorems were already well known to mathematicians.
Despite a number of extensive searches, the only known Wieferich primes to date are 1093 and 3511 .
was proven by Wieferich in 1909:
The above case (where p does not divide any of x, y or z) is commonly known as the first case of Fermat's Last Theorem (FLTI).
In 1910, Mirimanoff expanded the theorem by showing that, if the preconditions of the theorem hold true for some prime p, then p2 must also divide 3p − 1 − 1. Morishima
further proved that p2 must actually divide mp − 1 − 1 for every prime m ≤ 31. Granville and Monagan extended the proof to all m ≤ 89.
holds, then there exist infinitely many non-Wieferich primes. Numerical evidence suggests that very few of the prime numbers in a given interval are Wieferich primes. A proof of the abc conjecture would not automatically prove that there are only finitely many Wieferich primes, since the set of Wieferich primes and the set of non-Wieferich primes could possibly both be infinite and the finiteness or infiniteness of the set of Wieferich primes would have to be proven separately.
implies that if p > 2 is prime, then Mp−1 (= 2p − 1 − 1) is always divisible by p. Since Mersenne numbers of prime indices Mp and Mq are co-prime,
Thus, a Mersenne prime cannot also be a Wieferich prime. A notable open problem
is to determine whether or not all Mersenne numbers of prime index are square-free
. If a Mersenne number Mq is not square-free, i.e., there exists a prime p for which p2 divides Mq, then p is a Wieferich prime. Therefore, if there are only finitely many Wieferich primes, then there will be at most finitely many Mersenne numbers that are not square-free. It was observed that M1092 is divisible by 10932 and M3510 is divisible by 35112.
Similarly, if p is prime and p2 divides some Fermat number Fn = 22n + 1, then p must be a Wieferich prime.
in 1922, respectively. Around 1980, Lehmer was able to reach the search limit of 6. This limit was extended above 2.5 in 2006. It is now known, that if any other Wieferich primes exist, they must be greater than 6.7. The search for new Wieferich primes is currently performed by the distributed computing
project Wieferich@Home
.
It has been conjecture
d that only finitely many Wieferich primes exist. It has also been conjectured (as for Wilson prime
s) that infinitely many Wieferich primes exist, and that the number of Wieferich primes below x is approximately log log x, which is a heuristic result
that follows from the plausible assumption that for a prime p, the (p − 1)-th degree roots of unity modulo p2 are uniformly distributed in the multiplicative group of integers modulo p2
.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, a Wieferich prime is a prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p such that p2 divides 2p − 1 − 1, therefore connecting these primes with Fermat's little theorem
Fermat's little theorem
Fermat's little theorem states that if p is a prime number, then for any integer a, a p − a will be evenly divisible by p...
, which states that every odd prime p divides 2p − 1 − 1. Wieferich primes were first described by Arthur Wieferich
Arthur Wieferich
Arthur Josef Alwin Wieferich was a German mathematician and teacher, remembered for his work on number theory....
in 1909 in works pertaining to Fermat's last theorem
Fermat's Last Theorem
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
, at which time both theorems were already well known to mathematicians.
Despite a number of extensive searches, the only known Wieferich primes to date are 1093 and 3511 .
Connection with Fermat's last theorem
The following theorem connecting Wieferich primes and Fermat's last theoremFermat's Last Theorem
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
was proven by Wieferich in 1909:
- Let p be prime, and let x, y, z be integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s such that xp + yp + zp = 0. Furthermore, assume that p does not divide the productProduct (mathematics)In mathematics, a product is the result of multiplying, or an expression that identifies factors to be multiplied. The order in which real or complex numbers are multiplied has no bearing on the product; this is known as the commutative law of multiplication...
xyz. Then p is a Wieferich prime.
The above case (where p does not divide any of x, y or z) is commonly known as the first case of Fermat's Last Theorem (FLTI).
In 1910, Mirimanoff expanded the theorem by showing that, if the preconditions of the theorem hold true for some prime p, then p2 must also divide 3p − 1 − 1. Morishima
Taro Morishima
was a Japanese mathematician specializing in algebra who attended University of Tokyo in Japan. Morishima published at least thirteen papers, including his work on Fermat's Last Theorem. and a collected works volume published in 1990 after his death. He also corresponded several times with American...
further proved that p2 must actually divide mp − 1 − 1 for every prime m ≤ 31. Granville and Monagan extended the proof to all m ≤ 89.
Connection with the abc conjecture
A non-Wieferich prime is a prime p satisfying 2p − 1 ≢ 1 (mod p2). Silverman showed in 1988 that if the abc conjectureAbc conjecture
The abc conjecture is a conjecture in number theory, first proposed by Joseph Oesterlé and David Masser in 1985. The conjecture is stated in terms of three positive integers, a, b and c , which have no common factor and satisfy a + b = c...
holds, then there exist infinitely many non-Wieferich primes. Numerical evidence suggests that very few of the prime numbers in a given interval are Wieferich primes. A proof of the abc conjecture would not automatically prove that there are only finitely many Wieferich primes, since the set of Wieferich primes and the set of non-Wieferich primes could possibly both be infinite and the finiteness or infiniteness of the set of Wieferich primes would have to be proven separately.
Connection with Mersenne primes and Fermat primes
It is known that the nth Mersenne number Mn = 2n − 1 is prime only if n is prime. Fermat's little theoremFermat's little theorem
Fermat's little theorem states that if p is a prime number, then for any integer a, a p − a will be evenly divisible by p...
implies that if p > 2 is prime, then Mp−1 (= 2p − 1 − 1) is always divisible by p. Since Mersenne numbers of prime indices Mp and Mq are co-prime,
-
- A prime divisor p of Mq, where q is prime, is a Wieferich prime if and only if p2 divides Mq.
Thus, a Mersenne prime cannot also be a Wieferich prime. A notable open problem
Unsolved problems in mathematics
This article lists some unsolved problems in mathematics. See individual articles for details and sources.- Millennium Prize Problems :Of the seven Millennium Prize Problems set by the Clay Mathematics Institute, six have yet to be solved:* P versus NP...
is to determine whether or not all Mersenne numbers of prime index are square-free
Square-free integer
In mathematics, a square-free, or quadratfrei, integer is one divisible by no perfect square, except 1. For example, 10 is square-free but 18 is not, as it is divisible by 9 = 32...
. If a Mersenne number Mq is not square-free, i.e., there exists a prime p for which p2 divides Mq, then p is a Wieferich prime. Therefore, if there are only finitely many Wieferich primes, then there will be at most finitely many Mersenne numbers that are not square-free. It was observed that M1092 is divisible by 10932 and M3510 is divisible by 35112.
Similarly, if p is prime and p2 divides some Fermat number Fn = 22n + 1, then p must be a Wieferich prime.
Other properties
- Johnson observed that the two known Wieferich primes are one greater than numbers with periodic binary expansions (
; 
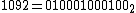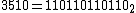). The Wieferich@HomeWieferich@HomeWieferich@Home is a distributed computing project searching for Wieferich primes. It is the first Czech distributed computing project. The only known Wieferich primes are 1093 and 3511, found in 1913 and 1922, respectively. It is not known if there exist infinitely or finitely many Wieferich...
project searches for Wieferich primes by testing numbers that are one greater than a number with a periodic binary expansion, but up to a total binary expansion length of 3500 and up to a period length of 24 it has not found a new Wieferich prime.
- If p is a Wieferich prime, then 2p ≡ 2 (mod p2) and thus 2p2 ≡ 2 (mod p2).
Search and current status
The only known Wieferich primes 1093 and 3511 were found by W. Meissner in 1913 and N. G. W. H. BeegerN. G. W. H. Beeger
Nicolaas George Wijnand Henri Beeger was a Dutch mathematician. His 1916 doctorate was on Dirichlet series. He worked for most of his life as a teacher, working on mathematics papers in his spare evenings...
in 1922, respectively. Around 1980, Lehmer was able to reach the search limit of 6. This limit was extended above 2.5 in 2006. It is now known, that if any other Wieferich primes exist, they must be greater than 6.7. The search for new Wieferich primes is currently performed by the distributed computing
Distributed computing
Distributed computing is a field of computer science that studies distributed systems. A distributed system consists of multiple autonomous computers that communicate through a computer network. The computers interact with each other in order to achieve a common goal...
project Wieferich@Home
Wieferich@Home
Wieferich@Home is a distributed computing project searching for Wieferich primes. It is the first Czech distributed computing project. The only known Wieferich primes are 1093 and 3511, found in 1913 and 1922, respectively. It is not known if there exist infinitely or finitely many Wieferich...
.
It has been conjecture
Conjecture
A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...
d that only finitely many Wieferich primes exist. It has also been conjectured (as for Wilson prime
Wilson prime
A Wilson prime, named after English mathematician John Wilson, is a prime number p such that p2 divides ! + 1, where "!" denotes the factorial function; compare this with Wilson's theorem, which states that every prime p divides ! + 1.The only known Wilson primes are 5, 13, and...
s) that infinitely many Wieferich primes exist, and that the number of Wieferich primes below x is approximately log log x, which is a heuristic result
Heuristic argument
A heuristic argument is an argument that reasons from the value of a method or principle that has been shown by experimental investigation to be a useful aid in learning, discovery and problem-solving. A widely-used and important example of a heuristic argument is Occam's Razor....
that follows from the plausible assumption that for a prime p, the (p − 1)-th degree roots of unity modulo p2 are uniformly distributed in the multiplicative group of integers modulo p2
Multiplicative group of integers modulo n
In modular arithmetic the set of congruence classes relatively prime to the modulus n form a group under multiplication called the multiplicative group of integers modulo n. It is also called the group of primitive residue classes modulo n. In the theory of rings, a branch of abstract algebra, it...
.
Generalizations
- A prime p satisfying the congruence 2(p−1)/2 ≡ ±1 + Ap (mod p2) with small |A| is commonly called a near-Wieferich prime . Near-Wieferich primes with A = 0 represent Wieferich primes. Recent searches, in addition to their primary search for Wieferich primes, also tried to find near-Wieferich primes. The following table lists all near-Wieferich primes with |A| ≤ 10 up to 3×1015. This search bound was reached in 2006 in a search effort by P. Carlisle, R. Crandall and M. Rodenkirch.
p 1 or −1 A 1093 +1 0 3511 +1 0 46262476201 +1 +5 47004625957 −1 +1 58481216789 −1 +5 76843523891 −1 +1 1180032105761 +1 −6 12456646902457 +1 +2 134257821895921 +1 +10 339258218134349 −1 +2 2276306935816523 −1 −3
- Dorais and Klyve used a different definition of a near-Wieferich prime, defining it as a prime p with small value of
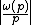where 
is the Fermat quotient of p modulo p (the modulo operationModulo operationIn computing, the modulo operation finds the remainder of division of one number by another.Given two positive numbers, and , a modulo n can be thought of as the remainder, on division of a by n...
here gives the residue with the smallest absolute value). The following table lists all primes p ≤ 6.7 × 1015 with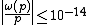
.
| p |  | |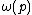
|---|---|---|
| 1093 | 0 | 0 |
| 3511 | 0 | 0 |
| 2276306935816523 | +6 | 0.264 |
| 3167939147662997 | −17 | 0.537 |
| 3723113065138349 | −36 | 0.967 |
| 5131427559624857 | −36 | 0.702 |
| 5294488110626977 | −31 | 0.586 |
| 6517506365514181 | +58 | 0.890 |
- A Wieferich prime base a is a prime p that satisfies
- ap − 1 ≡ 1 (mod p2).
- Such a prime cannot divide a, since then it would also divide 1. For the known Wieferich primes base a with small prime values of a, see Fermat quotient.
- A Wieferich pairWieferich pairIn mathematics, a Wieferich pair is a pair of prime numbers p and q that satisfyWieferich pairs are named after German mathematician Arthur Wieferich.There are only six Wieferich pairs known:...
is a pair of primes p and q that satisfy- pq − 1 ≡ 1 (mod q2) and qp − 1 ≡ 1 (mod p2)
- so that a Wieferich prime p ≡ 1 (mod 4) will form such a pair (p, 2): the only known instance in this case is p = 1093. There are 6 known Wieferich pairs.
See also
- Wall–Sun–Sun prime - a hypothetical type of prime number defined in the study of Fermat's last theorem Fermat's Last TheoremIn number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
(FLT) - Wolstenholme primeWolstenholme primeIn number theory, a Wolstenholme prime is a special type of prime number satisfying a stronger version of Wolstenholme's theorem. Wolstenholme's theorem is a congruence relation satisfied by all prime numbers greater than 7...
- another type of prime number which in the broadest sense also resulted from the study of FLT - List of near Wieferich primes - lists all near Wieferich primes up to 3