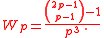Wolstenholme prime
Encyclopedia
In number theory
, a Wolstenholme prime is a special type of prime number
satisfying a stronger version of Wolstenholme's theorem. Wolstenholme's theorem is a congruence relation
satisfied by all prime numbers greater than 7. Wolstenholme primes are named after mathematician Joseph Wolstenholme
, who first described this theorem in the 19th century.
Interest in these primes first arose due to their connection with Fermat's last theorem
, another theorem with significant importance in mathematics. Wolstenholme primes are also related to other special classes of numbers, studied in the hope to be able to generalize a proof for the truth of the theorem to all positive integers greater than two.
The only two known Wolstenholme primes are 16843 and 2124679 . There are no other Wolstenholme primes less than 109.
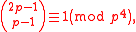
where the expression in left-hand side denotes a binomial coefficient
.
Compare this with Wolstenholme's theorem, which states that for every prime p > 3 the following congruence holds: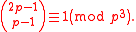
Bp−3. The Wolstenholme primes therefore form a subset of the irregular primes.
i.e. the numerator of the harmonic number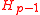
is divisible by p3.
. For each prime p ≥ 5, the Wolstenholme quotient is defined as
Clearly, p is a Wolstenholme prime if and only if Wp ≡ 0 (mod p). Empirically
one may assume that the remainder of Wp modulo p is uniformly distributed in the set {0, 1, …, p–1}. By this reasoning, the probability that the remainder takes on a particular value (e.g., 0) is about 1/p.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, a Wolstenholme prime is a special type of prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
satisfying a stronger version of Wolstenholme's theorem. Wolstenholme's theorem is a congruence relation
Congruence relation
In abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
satisfied by all prime numbers greater than 7. Wolstenholme primes are named after mathematician Joseph Wolstenholme
Joseph Wolstenholme
Joseph Wolstenholme was an English mathematician.Wolstenholme was born in Eccles near Salford, Lancashire, England. He graduated from St John's College, Cambridge as Third Wrangler in 1850 and was elected a fellow of Christ's College in 1852...
, who first described this theorem in the 19th century.
Interest in these primes first arose due to their connection with Fermat's last theorem
Fermat's Last Theorem
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
, another theorem with significant importance in mathematics. Wolstenholme primes are also related to other special classes of numbers, studied in the hope to be able to generalize a proof for the truth of the theorem to all positive integers greater than two.
The only two known Wolstenholme primes are 16843 and 2124679 . There are no other Wolstenholme primes less than 109.
Definition
Wolstenholme prime can be defined in a number of equivalent ways.Definition via binomial coefficients
A Wolstenholme prime is a prime number p > 7 that satisfies the congruenceCongruence relation
In abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
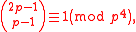
where the expression in left-hand side denotes a binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
.
Compare this with Wolstenholme's theorem, which states that for every prime p > 3 the following congruence holds:
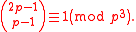
Definition via Bernoulli numbers
A Wolstenholme prime is a prime p that divides the numerator of the Bernoulli numberBernoulli number
In mathematics, the Bernoulli numbers Bn are a sequence of rational numbers with deep connections to number theory. They are closely related to the values of the Riemann zeta function at negative integers....
Bp−3. The Wolstenholme primes therefore form a subset of the irregular primes.
Definition via irregular pairs
A Wolstenholme prime is a prime p such that (p, p–3) is an irregular pair.Definition via harmonic numbers
A Wolstenholme prime is a prime p such thati.e. the numerator of the harmonic number
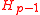is divisible by p3.Search and current status
The search for Wolstenholme primes began in the 1960s and continued over the following decades, with the latest results published in 2007. The first Wolstenholme prime 16843 was found in 1964, although it was not explicitly reported at that time. The 1964 discovery was later independently confirmed in the 1970s. This remained the only known example of such a prime for almost 20 years, until the discovery announcement of the second Wolstenholme prime 2124679 in 1993. Up to 1.2, no further Wolstenholme primes were found. This was later extended to 2 by McIntosh in 1995 and Trevisan & Weber were able to reach 2.5. The latest result is that there are only those two Wolstenholme primes up to .Expected number of Wolstenholme primes
It is conjectured that infinitely many Wolstenholme primes exist. It is conjectured that the number of Wolstenholme primes ≤ x is about ln ln x, where ln denotes the natural logarithmNatural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
. For each prime p ≥ 5, the Wolstenholme quotient is defined as
Clearly, p is a Wolstenholme prime if and only if Wp ≡ 0 (mod p). Empirically
Empirical relationship
In science, an empirical relationship is one based solely on observation rather than theory. An empirical relationship requires only confirmatory data irrespective of theoretical basis. Sometimes theoretical explanations for what were initially empirical relationships are found, in which case the...
one may assume that the remainder of Wp modulo p is uniformly distributed in the set {0, 1, …, p–1}. By this reasoning, the probability that the remainder takes on a particular value (e.g., 0) is about 1/p.
External links
- Caldwell, Chris K. Wolstenholme prime from The Prime Glossary
- McIntosh, R. J. Wolstenholme Search Status as of March 2004 e-mail to Paul Zimmermann
- Bruck, R. Wolstenholme's Theorem, Stirling Numbers, and Binomial Coefficients
- Conrad, K. The p-adic Growth of Harmonic Sums interesting observation involving the two Wolstenholme primes