Fermi-Walker transport
Encyclopedia
Fermi-Walker transport is a process in general relativity
used to define a coordinate system
or reference frame
such that all curvature
in the frame is due to the presence of mass/energy density and not to arbitrary spin or rotation of the frame.
This is defined for a vector field X along a curve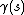
:
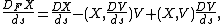
where V is four-velocity, D is the covariant derivative in the Riemannian space
, and is scalar product. If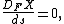
the vector field X is Fermi-Walker transported along the curve (see Hawking and Ellis, p. 80). Vectors tangent to the space of four-velocities in Minkowski spacetime, e.g., polarization vectors, under Fermi-Walker transport experience Thomas precession
.
Using the Fermi derivative, the Bargmann-Michel-Telegdi equation for spin precession of electron in an external electromagnetic field can be written as follows: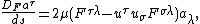
where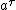
and 
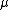are polarization four-vector and magnetic moment, 
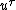is four-velocity of electron, 
, 
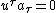, and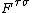 
is electromagnetic field-strength tensor. The right side describes Larmor precession
.
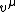as defining an axis in the co-moving coordinate system, then any system transforming with proper time is said to be undergoing Fermi Walker transport.
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
used to define a coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
or reference frame
Reference frame
Reference frame may refer to:*Frame of reference, in physics*Reference frame , frames of a compressed video that are used to define future frames...
such that all curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
in the frame is due to the presence of mass/energy density and not to arbitrary spin or rotation of the frame.
Fermi-Walker differentiation
In the theory of Lorentzian manifolds, Fermi-Walker differentiation is a generalization of covariant differentiation. In general relativity, Fermi-Walker derivatives of the spacelike unit vector fields in a frame field, taken with respect to the timelike unit vector field in the frame field, are used to define non-inertial but nonspinning frames, by stipulating that the Fermi-Walker derivatives should vanish. In the special case of inertial frames, the Fermi-Walker derivatives reduce to covariant derivatives.This is defined for a vector field X along a curve
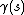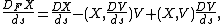
:where V is four-velocity, D is the covariant derivative in the Riemannian space
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
, and is scalar product. If
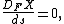
the vector field X is Fermi-Walker transported along the curve (see Hawking and Ellis, p. 80). Vectors tangent to the space of four-velocities in Minkowski spacetime, e.g., polarization vectors, under Fermi-Walker transport experience Thomas precession
Thomas precession
In physics the Thomas precession, named after Llewellyn Thomas, is a special relativistic correction that applies to the spin of an elementary particle or the rotation of a macroscopic gyroscope and relates the angular velocity of the spin of a particle following a curvilinear orbit to the angular...
.
Using the Fermi derivative, the Bargmann-Michel-Telegdi equation for spin precession of electron in an external electromagnetic field can be written as follows:
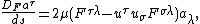
where
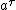and 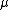are polarization four-vector and magnetic moment, 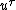is four-velocity of electron, , , 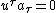and 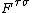is electromagnetic field-strength tensor. The right side describes Larmor precessionLarmor precession
In physics, Larmor precession is the precession of the magnetic moments of electrons, atomic nuclei, and atoms about an external magnetic field...
.
Co-moving coordinate systems
A coordinate system co-moving with the particle can be defined. If we take the unit vector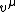 as defining an axis in the co-moving coordinate system, then any system transforming with proper time is said to be undergoing Fermi Walker transport. See also
- Basic introduction to the mathematics of curved spacetimeBasic introduction to the mathematics of curved spacetimeThe mathematics of general relativity are very complex. In Newton's theories of motions, an object's mass and length remain constant as it changes speed, and the rate of passage of time also remains unchanged. As a result, many problems in Newtonian mechanics can be solved with algebra alone...
- Enrico FermiEnrico FermiEnrico Fermi was an Italian-born, naturalized American physicist particularly known for his work on the development of the first nuclear reactor, Chicago Pile-1, and for his contributions to the development of quantum theory, nuclear and particle physics, and statistical mechanics...
- Transition from Newtonian mechanics to General relativity