Fernique's theorem
Encyclopedia
In mathematics
— specifically, in measure theory — Fernique's theorem is a result about Gaussian measure
s on Banach space
s. It extends the finite-dimensional result that a Gaussian random variable
has exponential
tails. The result was proved in 1970 by the mathematician
Xavier Fernique
.
defined on the Borel set
s of X such that, for every bounded linear functional ℓ : X → R, the push-forward measure ℓ∗μ defined on the Borel sets of R by
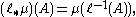
is a Gaussian measure (a normal distribution) with zero mean
. Then there exists α > 0 such that
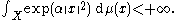
A fortiori, μ (equivalently, any X-valued random variable G whose law
is μ) has moments
of all orders: for all k ≥ 0,
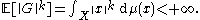
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
— specifically, in measure theory — Fernique's theorem is a result about Gaussian measure
Gaussian measure
In mathematics, Gaussian measure is a Borel measure on finite-dimensional Euclidean space Rn, closely related to the normal distribution in statistics. There is also a generalization to infinite-dimensional spaces...
s on Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s. It extends the finite-dimensional result that a Gaussian random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
has exponential
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
tails. The result was proved in 1970 by the mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Xavier Fernique
Xavier Fernique
Xavier Fernique is a mathematician, noted mostly for his contributions to the theory of stochastic processes. Fernique's theorem, a result on the integrability of Gaussian measures, is named after him.-External links:...
.
Statement of the theorem
Let (X, || ||) be a separable Banach space. Let μ be a centred Gaussian measure on X, i.e. a probability measureProbability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
defined on the Borel set
Borel set
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
s of X such that, for every bounded linear functional ℓ : X → R, the push-forward measure ℓ∗μ defined on the Borel sets of R by
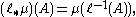
is a Gaussian measure (a normal distribution) with zero mean
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
. Then there exists α > 0 such that
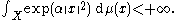
A fortiori, μ (equivalently, any X-valued random variable G whose law
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
is μ) has moments
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
of all orders: for all k ≥ 0,