
Feynman checkerboard
Encyclopedia
Richard Feynman
Richard Phillips Feynman was an American physicist known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics and the physics of the superfluidity of supercooled liquid helium, as well as in particle physics...
’s sum-over-paths
Path integral formulation
The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
formulation of the kernel for a free spin ½
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
particle moving in one spatial dimension. It provides a representation of solutions of the Dirac equation
Dirac equation
The Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
in (1+1)-dimensional spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
as discrete sums.
The model can be visualised by considering relativistic random walk
Random walk
A random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
s on a two-dimensional spacetime checkerboard. At each discrete timestep
 the particle of mass
the particle of mass  moves a distance
moves a distance  (
( being the speed of light
being the speed of lightSpeed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
) to the left or right. For such a discrete motion the Feynman path integral
Path integral formulation
The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
reduces to a sum over the possible paths. Feynman demonstrated that if each 'turn' (change of moving from left to right or vice versa) of the spacetime path is weighted by
 (with
(with 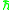 denoting the reduced Planck's constant), in the limit of vanishing checkerboard squares the sum of all weighted paths yields a propagator that satisfies the one-dimensional Dirac equation. As a result, helicity (the one-dimensional equivalent of spin
denoting the reduced Planck's constant), in the limit of vanishing checkerboard squares the sum of all weighted paths yields a propagator that satisfies the one-dimensional Dirac equation. As a result, helicity (the one-dimensional equivalent of spinSpin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
) is obtained from a simple cellular-automata
Cellular automaton
A cellular automaton is a discrete model studied in computability theory, mathematics, physics, complexity science, theoretical biology and microstructure modeling. It consists of a regular grid of cells, each in one of a finite number of states, such as "On" and "Off"...
type rule.
The Checkerboard model is important because it connects aspects of spin and chirality with propagation in spacetime and is the only sum-over-path formulation in which quantum phase is discrete at the level of the paths, taking only values corresponding to the 4th roots of unity.
History
Feynman invented the model in the 1940s while developing his spacetime approach to quantum mechanics.He did not publish the result until it appeared in a text on path-integrals coauthored by Albert Hibbs
Albert Hibbs
Albert Roach Hibbs was a noted mathematician known worldwide as "the voice of JPL". He was born in Akron, Ohio on October 19, 1924 and died on February 24, 2003 of complications following heart surgery....
in the mid 1960s. The model was not included with the original path-integral paper because a suitable generalization to a four dimensional spacetime had not been found.
One of the first connections between the amplitudes prescribed by Feynman for the Dirac particle in 1+1 dimensions, and the standard interpretation of amplitudes in terms of the Kernel or propagator, was established by Narlikar in a detailed analysis. The name 'Feynman Chessboard Model' was coined by Gersch when he demonstrated its relationship to the one-dimensional Ising model
Ising model
The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
. Gaveau et al. discovered a relationship between the model and a stochastic model of the Telegraph equations due to Mark Kac
Mark Kac
Mark Kac was a Polish mathematician. His main interest was probability theory. His question, "Can one hear the shape of a drum?" set off research into spectral theory, with the idea of understanding the extent to which the spectrum allows one to read back the geometry. Kac completed his Ph.D...
through analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
. Jacobson and Schulman examined the passage from the relativistic to the non-relativistic path integral. Subsequently Ord showed that the Chessboard model was embedded in correlations in Kac’s original stochastic model and so had a purely classical context, free of formal analytic continuation. In the same year, Kauffman and Noyesproduced a fully discrete version related to bit-string physics
Bit-string physics
Bit-string physics is an emerging body of theory which considers the universe to be a process of operations on strings of bits. Bit-string physics is often associated with A.F. Parker-Rhodes' combinatorial hierarchy, which is notable for its relationship with the electromagnetic and gravitational...
, that has recently been developed into a general approach to discrete physics.
Extensions
Although Feynman did not live to publish extensions to the Chessboard model, it is evident from his archived notes that he was interested in establishing a link between the 4th roots of unity (used as statistical weights in chessboard paths) and his discovery, with J. A. WheelerJohn Archibald Wheeler
John Archibald Wheeler was an American theoretical physicist who was largely responsible for reviving interest in general relativity in the United States after World War II. Wheeler also worked with Niels Bohr in explaining the basic principles behind nuclear fission...
, that antiparticles are equivalent to particles moving backwards in time. His notes contain several sketches of chessboard paths with added spacetime loops. The first extension of the model to explicitly contain such loops was the ‘Spiral Model' in which chessboard paths were allowed to spiral in spacetime. Unlike the Chessboard case, causality
Causality (physics)
Causality is the relationship between causes and effects. It is considered to be fundamental to all natural science, especially physics. Causality is also a topic studied from the perspectives of philosophy and statistics....
had to be implemented explicitly to avoid divergences, however with this restriction the Dirac equation emerged as a continuum limit. Subsequently the roles of Zitterbewegung
Zitterbewegung
Zitterbewegung is a theoretical rapid motion of elementary particles, in particular electrons, that obey the Dirac equation...
, antiparticles and the Dirac Sea
Dirac sea
The Dirac sea is a theoretical model of the vacuum as an infinite sea of particles with negative energy. It was first postulated by the British physicist Paul Dirac in 1930 to explain the anomalous negative-energy quantum states predicted by the Dirac equation for relativistic electrons...
in the Chessboard model have been elucidated and the implications for the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
considered through the non-relativistic limit.
Further extensions of the original 2-dimensional spacetime model include features such as improved summation rules and generalized lattices.There has been no consensus on an optimal extension of the Chessboard model to a fully four-dimensional space-time. Two distinct classes of extensions exist, those working with a fixed underlying lattice and those that embed the two dimensional case in higher dimension. The advantage of the former is that the sum-over-paths is closer to the non-relativistic case, however the simple picture of a single directionally independent speed of light is lost. In the latter extensions the fixed speed property is maintained at the expense of variable directions at each step.

