
Final value theorem
Encyclopedia
In mathematical analysis
, the final value theorem (FVT) is one of several similar theorems used to relate frequency domain
expressions to the time domain
behavior as time approaches infinity. A final value theorem allows the time domain behavior to be directly calculated by taking a limit of a frequency domain expression, as opposed to converting to a time domain expression and taking its limit.
Mathematically, if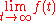
has a finite limit, then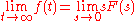
where is the (unilateral) Laplace transform of
is the (unilateral) Laplace transform of 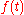 .
.

and so the impulse response
converges to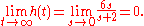
That is, the system returns to zero after being disturbed by a short impulse. However, the Laplace transform of the unit step response
is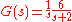
and so the step response converges to
and so a zero-state system will follow an exponential rise to a final value of 3.
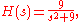
the final value theorem appears to predict the final value of the impulse response to be 0 and the final value of the step response to be 1. However, neither time-domain limit exists, and so the final value theorem predictions are not valid. In fact, both the impulse response and step response oscillate, and (in this special case) the final value theorem describes the average values around which the responses oscillate.
There are two checks performed in Control theory
which confirm valid results for the Final Value Theorem:
Rule 1 was not satisfied in this example, in that the roots of the denominator are and
and  .
.
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, the final value theorem (FVT) is one of several similar theorems used to relate frequency domain
Frequency domain
In electronics, control systems engineering, and statistics, frequency domain is a term used to describe the domain for analysis of mathematical functions or signals with respect to frequency, rather than time....
expressions to the time domain
Time domain
Time domain is a term used to describe the analysis of mathematical functions, physical signals or time series of economic or environmental data, with respect to time. In the time domain, the signal or function's value is known for all real numbers, for the case of continuous time, or at various...
behavior as time approaches infinity. A final value theorem allows the time domain behavior to be directly calculated by taking a limit of a frequency domain expression, as opposed to converting to a time domain expression and taking its limit.
Mathematically, if
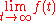
has a finite limit, then
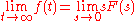
where
 is the (unilateral) Laplace transform of
is the (unilateral) Laplace transform of 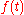 .
.Example where FVT holds
For example, for a system described by transfer functionTransfer function
A transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...

and so the impulse response
Impulse response
In signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...
converges to
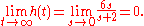
That is, the system returns to zero after being disturbed by a short impulse. However, the Laplace transform of the unit step response
Step response
The step response of a system in a given initial state consists of the time evolution of its outputs when its control inputs are Heaviside step functions. In electronic engineering and control theory, step response is the time behaviour of the outputs of a general system when its inputs change from...
is
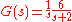
and so the step response converges to

and so a zero-state system will follow an exponential rise to a final value of 3.
Example where FVT does not hold
However, for a system described by the transfer function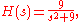
the final value theorem appears to predict the final value of the impulse response to be 0 and the final value of the step response to be 1. However, neither time-domain limit exists, and so the final value theorem predictions are not valid. In fact, both the impulse response and step response oscillate, and (in this special case) the final value theorem describes the average values around which the responses oscillate.
There are two checks performed in Control theory
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
which confirm valid results for the Final Value Theorem:
- All roots of the denominator of
 must have negative real parts.
must have negative real parts. -
 must not have more than one pole at the origin.
must not have more than one pole at the origin.
Rule 1 was not satisfied in this example, in that the roots of the denominator are
 and
and  .
.External links
- http://wikis.controltheorypro.com/index.php?title=Final_Value_Theorem
- http://fourier.eng.hmc.edu/e102/lectures/Laplace_Transform/node17.html Final value for Laplace
- http://www.engr.iupui.edu/~skoskie/ECE595s7/handouts/fvt_proof.pdf Final value proof for Z-transforms

