The firehose instability (or hose-pipe instability) is a dynamical instability

Instability

In numerous fields of study, the component of instability within a system is generally characterized by some of the outputs or internal states growing without bounds...

 of thin or elongated galaxies. The instability causes the galaxy to buckle or bend in a direction perpendicular to its long axis. After the instability has run its course, the galaxy is less elongated (i.e. rounder) than before. Any sufficiently thin stellar system, in which some component of the internal velocity is in the form of random or counter-streaming motions (as opposed to rotation

Rotation

A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...

), is subject to the instability.

The firehose instability is probably responsible for the fact that elliptical galaxies and dark matter halo

Dark matter halo

A dark matter halo is a hypothetical component of a galaxy, which extends beyond the edge of the visible galaxy and dominates the total mass. Since they consist of dark matter, halos cannot be observed directly, but their existence is inferred through their effects on the motions of stars and gas...

es never have axis ratios more extreme than about 3:1, since this is roughly the axis ratio at which the instability sets in. It may also play a role in the formation of barred spiral galaxies

Barred spiral galaxy

A barred spiral galaxy is a spiral galaxy with a central bar-shaped structure composed of stars. Bars are found in approximately two-thirds of all spiral galaxies...

, by causing the bar to thicken in the direction perpendicular to the galaxy disk.

The firehose instability derives its name from a similar instability in magnetized plasmas

Plasma (physics)

In physics and chemistry, plasma is a state of matter similar to gas in which a certain portion of the particles are ionized. Heating a gas may ionize its molecules or atoms , thus turning it into a plasma, which contains charged particles: positive ions and negative electrons or ions...

. However, from a dynamical point of view, a better analogy is with the Kelvin–Helmholtz instability, or with beads sliding along an oscillating string.

Stability analysis: sheets and wires

The firehose instability can be analyzed exactly in the case of an infinitely thin, self-gravitating sheet of stars. If the sheet experiences a small displacement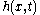 in the direction, the vertical acceleration for stars of velocity as they move around the bend is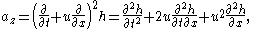


provided the bend is small enough that the horizontal velocity is unaffected. Averaged over all stars at , this acceleration must equal the gravitational restoring force per unit mass 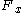. In a frame chosen such that the mean streaming motions are zero, this relation becomes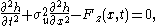


where 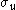is the horizontal velocity dispersion in that frame.

For a perturbation of the form
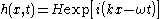
the gravitational restoring force is
where is the surface mass density. The dispersion relation

Dispersion relation

In physics and electrical engineering, dispersion most often refers to frequency-dependent effects in wave propagation. Note, however, that there are several other uses of the word "dispersion" in the physical sciences....

 for a thin self-gravitating sheet is then


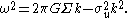
The first term, which arises from the perturbed gravity, is stabilizing, while the second term, due to the centrifugal force

Centrifugal force

Centrifugal force can generally be any force directed outward relative to some origin. More particularly, in classical mechanics, the centrifugal force is an outward force which arises when describing the motion of objects in a rotating reference frame...

 that the stars exert on the sheet, is destabilizing.

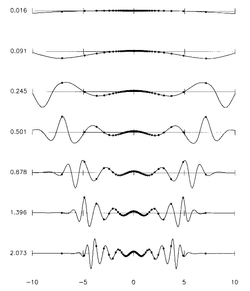
For sufficiently long wavelengths:


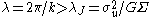
the gravitational restoring force dominates, and the sheet is stable; while at short wavelengths the sheet is unstable. The firehose instability is precisely complementary, in this sense, to the Jeans instability

Jeans instability

In physics, the Jeans instability causes the collapse of interstellar gas clouds and subsequent star formation. It occurs when the internal gas pressure is not strong enough to prevent gravitational collapse of a region filled with matter...

 in the plane, which is stabilized at short wavelengths, .

A similar analysis can be carried out for a galaxy that is idealized as a one-dimensional wire, with density that varies along the axis. This is a simple model of a (prolate) elliptical galaxy. Some unstable eigenmodes are shown in Figure 2 at left.

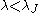Stability analysis: finite-thickness galaxies

At wavelengths shorter than the actual vertical thickness of a galaxy, the bending is stabilized. The reason is that stars in a finite-thickness galaxy oscillate vertically with an unperturbed frequency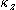 ; like any oscillator, the phase of the star's response to the imposed bending depends entirely on whether the forcing frequency 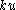is greater than or less than its natural frequency. If 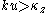for most stars, the overall density response to the perturbation will produce a gravitational potential opposite to that imposed by the bend and the disurbance will be damped. These arguments imply that a sufficiently thick galaxy (with low 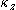) will be stable to bending at all wavelengths, both short and long.

Analysis of the linear normal modes of a finite-thickness slab shows that bending is indeed stabilized when the ratio of vertical to horizontal velocity dispersions exceeds about 0.3. Since the elongation of a stellar system with this anisotropy is approximately 15:1 — much more extreme than observed in real galaxies — bending instabilities were believed for many years to be of little importance. However, Fridman & Polyachenko showed that the critical axis ratio for stability of homogeneous (constant-density) oblate and prolate spheroids was roughly 3:1, not 15:1 as implied by the infinite slab, and Merritt & Hernquist found a similar result in an N-body

N-body simulation

An N-body simulation is a simulation of a dynamical system of particles, usually under the influence of physical forces, such as gravity . In cosmology, they are used to study processes of non-linear structure formation such as the process of forming galaxy filaments and galaxy halos from dark...

 study of inhomogeneous prolate spheroids (Fig. 1).

The discrepancy was resolved in 1994. The gravitational restoring force from a bend is substantially weaker in finite or inhomogeneous galaxies than in infinite sheets and slabs, since there is less matter at large distances to contribute to the restoring force. As a result, the long-wavelength modes are not stabilized by gravity, as implied by the dispersion relation derived above. In these more realistic models, a typical star feels a vertical forcing frequency from a long-wavelength bend that is roughly twice the frequency 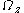of its unperturbed orbital motion along the long axis. Stability to global bending modes then requires that this forcing frequency be greater than , the frequency of orbital motion parallel to the short axis. The resulting (approximate) condition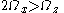


predicts stability for homogeneous prolate spheroids rounder than 2.94:1, in excellent agreement with the normal-mode calculations of Fridman & Polyachenko and with N-body simulations of homogeneous oblate and inhomogeneous prolate galaxies.

The situation for disk

Spiral galaxy

A spiral galaxy is a certain kind of galaxy originally described by Edwin Hubble in his 1936 work The Realm of the Nebulae and, as such, forms part of the Hubble sequence. Spiral galaxies consist of a flat, rotating disk containing stars, gas and dust, and a central concentration of stars known as...

 galaxies is more complicated, since the shapes of the dominant modes depend on whether the internal velocities are azimuthally or radially biased. In oblate galaxies with radially-elongated velocity ellipsoids, arguments similar to those given above suggest that an axis ratio of roughly 3:1 is again close to critical, in agreement with N-body simulations for thickened disks. If the stellar velocities are azimuthally biased, the orbits are approximately circular and so othe dominant modes are angular (corrugation) modes, 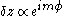. The approximate condition for stability becomes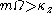


with 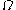the circular orbital frequency.

Importance

The firehose instability is believed to play an important role in determining the structure of both spiral

Spiral galaxy

A spiral galaxy is a certain kind of galaxy originally described by Edwin Hubble in his 1936 work The Realm of the Nebulae and, as such, forms part of the Hubble sequence. Spiral galaxies consist of a flat, rotating disk containing stars, gas and dust, and a central concentration of stars known as...

 and elliptical

Elliptical galaxy

An elliptical galaxy is a galaxy having an approximately ellipsoidal shape and a smooth, nearly featureless brightness profile. They range in shape from nearly spherical to highly flat and in size from hundreds of millions to over one trillion stars...

 galaxies and of dark matter halo

Dark matter halo

A dark matter halo is a hypothetical component of a galaxy, which extends beyond the edge of the visible galaxy and dominates the total mass. Since they consist of dark matter, halos cannot be observed directly, but their existence is inferred through their effects on the motions of stars and gas...

es.

• As noted by Edwin Hubble
  Edwin Hubble
  Edwin Powell Hubble was an American astronomer who profoundly changed the understanding of the universe by confirming the existence of galaxies other than the Milky Way - our own galaxy...
  
   and others, elliptical galaxies are rarely if ever observed to be more elongated than E6 or E7, corresponding to a maximum axis ratio of about 3:1. The firehose instability is probably responsible for this fact, since an elliptical galaxy that formed with an initially more elongated shape would be unstable to bending modes, causing it to become rounder.

• Simulated dark matter halo
  Dark matter halo
  A dark matter halo is a hypothetical component of a galaxy, which extends beyond the edge of the visible galaxy and dominates the total mass. Since they consist of dark matter, halos cannot be observed directly, but their existence is inferred through their effects on the motions of stars and gas...
  
  es, like elliptical galaxies, never have elongations greater than about 3:1. This is probably also a consequence of the firehose instability.

• N-body simulations reveal that the bars of barred spiral galaxies often "puff up" spontaneously, converting the initially thin bar into a bulge
  Bulge (astronomy)
  In astronomy, a bulge is a tightly packed group of stars within a larger formation. The term almost exclusively refers to the central group of stars found in most spiral galaxies...
  
   or thick disk
  Star count
  Star Counts are bookkeeping surveys of stars and the statistical and geometrical methods used to correct the survey data for bias. The surveys are most often made of nearby stars in the Milky Way Galaxy....
  
   subsystem. The bending instability is sometimes violent enough to destroy the bar completely. Bulges formed in this way are very "boxy" in appearance, similar to what is often observed.

• The firehose instability may play a role in the formation of galactic warps.