First-hitting-time model
Encyclopedia
In statistics
, first-hitting-time models are a sub-class of survival models
. The first hitting time, also called first passage time, of a set
with respect to an instance of a stochastic process
is the time until the stochastic process first enters
.
, such as Gambler's ruin
. In this example, an entity (often described as a gambler or an insurance company) has an amount of money which varies randomly with time, possibly with some drift
. The model considers the event that the amount of money reaches 0, representing bankruptcy. The model can answer questions such as the probability that this occurs within finite time, or the mean time until which it occurs.
First-hitting-time models can be applied to expected lifetimes, of patients or mechanical devices. When the process reaches an adverse threshold state for the first time, the patient dies, or the device breaks down.
A first-hitting-time (FHT) model has two underlying components: (1) a parent stochastic process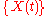
, and (2) a threshold. The first hitting time is defined as the time when the stochastic process first reaches the threshold. It is very important to distinguish whether the sample path of the parent process is latent (i.e., unobservable) or observable, and such distinction is a characteristic of the FHT model. By far, latent processes are most common. To give an example, we can use a Wiener process 
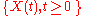as the parent stochastic process. Such Wiener process can be defined with the mean parameter 
, the variance parameter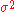 
, and the initial value 
.
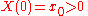Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, first-hitting-time models are a sub-class of survival models
Survival analysis
Survival analysis is a branch of statistics which deals with death in biological organisms and failure in mechanical systems. This topic is called reliability theory or reliability analysis in engineering, and duration analysis or duration modeling in economics or sociology...
. The first hitting time, also called first passage time, of a set
with respect to an instance of a stochastic processStochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
is the time until the stochastic process first enters
.Examples
A common example of a first-hitting-time model is a ruin problemRuin theory
Ruin theory, sometimes referred to as collective risk theory, is a branch of actuarial science that studies an insurer's vulnerability to insolvency based on mathematical modeling of the insurer's surplus....
, such as Gambler's ruin
Gambler's ruin
The term gambler's ruin is used for a number of related statistical ideas:* The original meaning is that a gambler who raises his bet to a fixed fraction of bankroll when he wins, but does not reduce it when he loses, will eventually go broke, even if he has a positive expected value on each bet.*...
. In this example, an entity (often described as a gambler or an insurance company) has an amount of money which varies randomly with time, possibly with some drift
Stochastic drift
In probability theory, stochastic drift is the change of the average value of a stochastic process. A related term is the drift rate which is the rate at which the average changes. This is in contrast to the random fluctuations about this average value...
. The model considers the event that the amount of money reaches 0, representing bankruptcy. The model can answer questions such as the probability that this occurs within finite time, or the mean time until which it occurs.
First-hitting-time models can be applied to expected lifetimes, of patients or mechanical devices. When the process reaches an adverse threshold state for the first time, the patient dies, or the device breaks down.
Latent vs observable
In many real world applications, the process is latent, or unobservable. When first hitting time models are equipped with regression structures, accommodating covariate data, we call such regression structure Threshold regression. The threshold state, parameters of the process, and even time scale may depend on corresponding covariates.A first-hitting-time (FHT) model has two underlying components: (1) a parent stochastic process
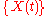, and (2) a threshold. The first hitting time is defined as the time when the stochastic process first reaches the threshold. It is very important to distinguish whether the sample path of the parent process is latent (i.e., unobservable) or observable, and such distinction is a characteristic of the FHT model. By far, latent processes are most common. To give an example, we can use a Wiener process 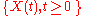as the parent stochastic process. Such Wiener process can be defined with the mean parameter , the variance parameter 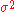, and the initial value .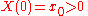