
Fisher-Tippett distribution
Encyclopedia
In probability theory
and statistics
, the Gumbel distribution (named after Emil Julius Gumbel
(1891–1966)) is used to model the distribution of the maximum (or the minimum) of a number of samples of various distributions.
For example we would use it to represent the distribution of the maximum level of a river in a particular year if we had the list of maximum values for the past ten years. It is useful in predicting the chance that an extreme earthquake, flood or other natural disaster will occur.
The potential applicability of the Gumbel distribution to represent the distribution of maxima relates to extreme value theory
which indicates that it is likely to be useful if the distribution of the underlying sample data is of the normal or exponential type.
The Gumbel distribution is a particular case of generalized extreme value distribution (also known as the Fisher-Tippett distribution) and the distribution is also known as the log-Weibull distribution and the double exponential distribution (which is sometimes used to refer to the Laplace distribution). It is often incorrectly labelled as Gompertz distribution.
of the Gumbel distribution is
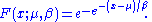
The median is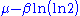
The mean is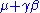 where
where 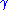 = Euler–Mascheroni constant
= Euler–Mascheroni constant  0.5772156649015328606.
0.5772156649015328606.
The standard deviation is
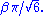
The mode is μ.
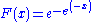
and probability density function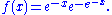
The median is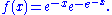 0.36651292058166432701.
0.36651292058166432701.
The mean is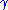 , the Euler–Mascheroni constant
, the Euler–Mascheroni constant  0.5772156649015328606.
0.5772156649015328606.
The standard deviation is
The mode is 0.
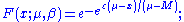

where M is the median
. To fit values one could get the median
straight away and then vary μ until it fits the list of values.
in the interval[0, 1] , the variate
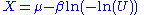
has a Gumbel distribution with parameters μ and β. This follows from the form of the cumulative distribution function given above.
 , then Y has a Gompertz distribution.
, then Y has a Gompertz distribution.
) in a sample of a random variable
following an exponential distribution
approaches the Gumbel distribution closer with increasing sample size.
In hydrology
, therefore, the Gumbel distribution is used to analyze such variables as monthly and annual maximum values of daily rainfall and river discharge volumes.
Gumbel has also shown that the estimator
r / (n+1) for the probability of an event - where r is the rank number of the observed value in the data series and n is the total number of observations - is an unbiased estimator of the cumulative probability around the mode
of the distribution. Therefore, this estimator is often used as a plotting position.
The blue picture illustrates an example of fitting the Gumbel distribution to ranked maximum one-day October rainfalls showing also the 90% confidence belt based on the binomial distribution. The rainfall data are represented by the plotting position r / (n+1) as part of the cumulative frequency analysis
.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the Gumbel distribution (named after Emil Julius Gumbel
Emil Julius Gumbel
Emil Julius Gumbel was a Jewish mathematician and political writer.Born in Munich, he graduated from the University of Munich shortly before the outbreak of the First World War...
(1891–1966)) is used to model the distribution of the maximum (or the minimum) of a number of samples of various distributions.
For example we would use it to represent the distribution of the maximum level of a river in a particular year if we had the list of maximum values for the past ten years. It is useful in predicting the chance that an extreme earthquake, flood or other natural disaster will occur.
The potential applicability of the Gumbel distribution to represent the distribution of maxima relates to extreme value theory
Extreme value theory
Extreme value theory is a branch of statistics dealing with the extreme deviations from the median of probability distributions. The general theory sets out to assess the type of probability distributions generated by processes...
which indicates that it is likely to be useful if the distribution of the underlying sample data is of the normal or exponential type.
The Gumbel distribution is a particular case of generalized extreme value distribution (also known as the Fisher-Tippett distribution) and the distribution is also known as the log-Weibull distribution and the double exponential distribution (which is sometimes used to refer to the Laplace distribution). It is often incorrectly labelled as Gompertz distribution.
Properties
The cumulative distribution functionCumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
of the Gumbel distribution is
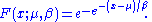
The median is
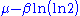
The mean is
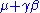 where
where 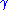 = Euler–Mascheroni constant
= Euler–Mascheroni constant  0.5772156649015328606.
0.5772156649015328606.The standard deviation is
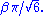
The mode is μ.
Standard Gumbel distribution
The standard Gumbel distribution is the case where μ = 0 and β = 1 with cumulative distribution function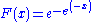
and probability density function
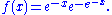
The median is
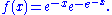 0.36651292058166432701.
0.36651292058166432701.The mean is
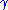 , the Euler–Mascheroni constant
, the Euler–Mascheroni constant  0.5772156649015328606.
0.5772156649015328606.The standard deviation is
-
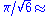 1.28254983016186409554.
1.28254983016186409554.
The mode is 0.
Parameter estimation
A more practical way of using the distribution could be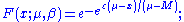

where M is the median
Median
In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
. To fit values one could get the median
straight away and then vary μ until it fits the list of values.
Generating Gumbel variates
Given a random variate U drawn from the uniform distributionUniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
in the interval
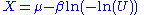
has a Gumbel distribution with parameters μ and β. This follows from the form of the cumulative distribution function given above.
Related distributions
When the cdf of Y is the converse of the Gumbel standard cumulative distribution, , then Y has a Gompertz distribution.
, then Y has a Gompertz distribution.Application
Gumbel has shown that the maximum value (or first order statisticOrder statistic
In statistics, the kth order statistic of a statistical sample is equal to its kth-smallest value. Together with rank statistics, order statistics are among the most fundamental tools in non-parametric statistics and inference....
) in a sample of a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
following an exponential distribution
Exponential distribution
In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
approaches the Gumbel distribution closer with increasing sample size.
In hydrology
Hydrology
Hydrology is the study of the movement, distribution, and quality of water on Earth and other planets, including the hydrologic cycle, water resources and environmental watershed sustainability...
, therefore, the Gumbel distribution is used to analyze such variables as monthly and annual maximum values of daily rainfall and river discharge volumes.
Gumbel has also shown that the estimator
Estimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
r / (n+1) for the probability of an event - where r is the rank number of the observed value in the data series and n is the total number of observations - is an unbiased estimator of the cumulative probability around the mode
Mode (statistics)
In statistics, the mode is the value that occurs most frequently in a data set or a probability distribution. In some fields, notably education, sample data are often called scores, and the sample mode is known as the modal score....
of the distribution. Therefore, this estimator is often used as a plotting position.
The blue picture illustrates an example of fitting the Gumbel distribution to ranked maximum one-day October rainfalls showing also the 90% confidence belt based on the binomial distribution. The rainfall data are represented by the plotting position r / (n+1) as part of the cumulative frequency analysis
Cumulative frequency analysis
Cumulative frequency analysis is the applcation of estimation theory to exceedance probability . The complement, the non-exceedance probability concerns the frequency of occurrence of values of a phenomenon staying below a reference value. The phenomenon may be time or space dependent...
.
See also
- Type-1 Gumbel distribution
- Type-2 Gumbel distribution
- Extreme value theoryExtreme value theoryExtreme value theory is a branch of statistics dealing with the extreme deviations from the median of probability distributions. The general theory sets out to assess the type of probability distributions generated by processes...
- Generalized extreme value distribution
- Fisher–Tippett–Gnedenko theorem
- CumFreqCumFreqIn statistics and data analysis the application software CumFreq is a free and user-friendly tool for cumulative frequency analysis of a single variable and for probability distribution fitting....
(application software for probability distributions including Gumbel)

