Flatness (systems theory)
Encyclopedia
Flatness in systems theory
is a system property that extends the notion of Controllability
from linear systems
to nonlinear
dynamical system
s. A system that has the flatness property is called a flat system. Flat systems have a (fictituous) flat output, which can be used to explicitly express all states and inputs in terms of the flat output and a finite number of its derivatives. Flatness in systems theory is based on the mathematical notion of flatness
in commutative algebra
and is applied in control theory
.
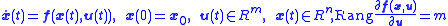
Is flat, if there exists an output
that satisfies the following conditions:
If these conditions are satisfied at least locally, then the (possibly fictitious) output is called flat output, and the system is flat.
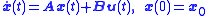
with the same signal dimensions for
as the nonlinear system is flat, if and only if it is controllable
. For linear systems
both properties are equivalent, hence exchangeable.
Systems theory
Systems theory is the transdisciplinary study of systems in general, with the goal of elucidating principles that can be applied to all types of systems at all nesting levels in all fields of research...
is a system property that extends the notion of Controllability
Controllability
Controllability is an important property of a control system, and the controllability property plays a crucial role in many control problems, such as stabilization of unstable systems by feedback, or optimal control....
from linear systems
LTI system theory
Linear time-invariant system theory, commonly known as LTI system theory, comes from applied mathematics and has direct applications in NMR spectroscopy, seismology, circuits, signal processing, control theory, and other technical areas. It investigates the response of a linear and time-invariant...
to nonlinear
Nonlinearity
In mathematics, a nonlinear system is one that does not satisfy the superposition principle, or one whose output is not directly proportional to its input; a linear system fulfills these conditions. In other words, a nonlinear system is any problem where the variable to be solved for cannot be...
dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
s. A system that has the flatness property is called a flat system. Flat systems have a (fictituous) flat output, which can be used to explicitly express all states and inputs in terms of the flat output and a finite number of its derivatives. Flatness in systems theory is based on the mathematical notion of flatness
Flat morphism
In mathematics, in particular in the theory of schemes in algebraic geometry, a flat morphism f from a scheme X to a scheme Y is a morphism such that the induced map on every stalk is a flat map of rings, i.e.,is a flat map for all P in X...
in commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
and is applied in control theory
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
.
Definition
A nonlinear system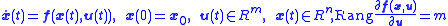Is flat, if there exists an output
that satisfies the following conditions:
- The signals
are representable as functions of the states 
and inputs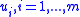 
and a finite number of derivatives with respect to time 
: 
.
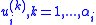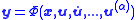- The states
and inputs 
are representable as functions of the outputs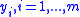 
and of its derivatives with respect to time 
.
- The components of
are differentially independent, that is, they satisfy no differential equation of the form 
.
If these conditions are satisfied at least locally, then the (possibly fictitious) output is called flat output, and the system is flat.
Relation to controllability of linear systems
A linear systemLTI system theory
Linear time-invariant system theory, commonly known as LTI system theory, comes from applied mathematics and has direct applications in NMR spectroscopy, seismology, circuits, signal processing, control theory, and other technical areas. It investigates the response of a linear and time-invariant...
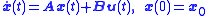
with the same signal dimensions for
as the nonlinear system is flat, if and only if it is controllableControllability
Controllability is an important property of a control system, and the controllability property plays a crucial role in many control problems, such as stabilization of unstable systems by feedback, or optimal control....
. For linear systems
LTI system theory
Linear time-invariant system theory, commonly known as LTI system theory, comes from applied mathematics and has direct applications in NMR spectroscopy, seismology, circuits, signal processing, control theory, and other technical areas. It investigates the response of a linear and time-invariant...
both properties are equivalent, hence exchangeable.
Significance
The flatness property is useful for both the analysis of and controller synthesis for nonlinear dynamical systems. it is particularly advantageous for solving trajectory planning problems and asymptotical setpoint following control.Literature
- M. Fliess, J. L. Lévine, P. Martin and P. Rouchon: Flatness and defect of non-linear systems: introductory theory and examples. International Journal of Control 61(6), pp. 1327-1361, 1995 http://cas.ensmp.fr/~rouchon/publications/PR1995/IJC95.pdf