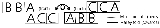
Flexagon
Encyclopedia
In geometry
, flexagons are flat models, usually constructed by folding strips of paper, that can be flexed or folded in certain ways to reveal faces besides the two that were originally on the back and front.
Flexagons are usually square or rectangular (tetraflexagons) or hexagonal (hexaflexagons). A prefix can be added to the name to indicate the number of faces that the model can display, including the two faces (back and front) that are visible before flexing. For example, a hexaflexagon with a total of six faces is called a hexahexaflexagon.
In hexaflexagon theory (that is, concerning flexagons with six sides), flexagons are usually defined in terms of pats.
Two flexagons are equivalent if one can be transformed to the other by a series of pinches and rotations. Flexagon equivalence is an equivalence relation
.
who was studying at Princeton University
in the USA
in 1939, allegedly while he was playing with the strips he had cut off his foolscap
paper to convert it to letter size
. Stone's colleagues Bryant Tuckerman
, Richard P. Feynman
and John W. Tukey became interested in the idea and formed the Princeton Flexagon Committee. Tuckerman worked out a topological
method, called the Tuckerman traverse, for revealing all the faces of a flexagon.
Flexagons were introduced to the general public by the recreational mathematician
Martin Gardner
, writing in 1956 in his inaugural "Mathematical Games" column for Scientific American
magazine.
applied for, and in 1959 were granted, U.S. Patent #2,883,185 for the hexahexaflexagon, under the title "Changeable Amusement Devices and the Like." The patent imagined possible applications of the device "as a toy, as an advertising display device, or as an educational geometric device." A few such novelties were produced by the Herbick & Held Printing Company
, the Pittsburgh printing firm where Rogers worked. But the device, marketed as the "Hexmo", failed to catch on commercially.
sides). The "tri" in the name means it has three faces, two of which are visible at any given time if the flexagon is pressed flat.
It is folded from a strip of six squares of paper like this:

To fold this shape into a tritetraflexagon, first crease each line between two squares. Then fold the mountain fold away from you and the valley fold towards you, and add a small piece of tape like this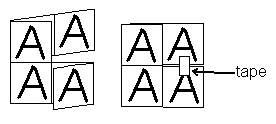
This figure has two faces visible, built of squares marked with "A"s and "B"s. The face of "C"s is hidden inside the flexagon. To reveal it, fold the flexagon flat and then unfold it, like this
The construction of the tritetraflexagon is similar to the mechanism used in the traditional Jacob's Ladder
children's toy, in Rubik's Magic
and in the magic wallet trick or the Himber
wallet.
Cyclic hexatetraflexagon doesn't have "dead ends" but you can keep folding it until you reach the starting position. If your colour the sides as you go, you can see the states more clearly.
While this is the simplest of the hexaflexagons to make and to manage, it is a very satisfying place to begin. It is made from a single strip of paper, divided into ten equilateral triangles. Patterns are available at The Flexagon Portal.
It is possible to automatically section and correctly place photographs (or drawings) of your own selection onto Trihexaflexagons using the simple program Foto-TriHexaFlexagon.

Make a mountain fold between the first 2 and the first 3. Continue folding in a spiral fashion, for a total of nine folds. You now have a straight strip with ten triangles on each side. There are two places where 3's are next to each other; fold in both these places so as to hide the 3's, forming a hexagon with a triangular tab sticking out. Lift one end of the hexagon around the other so that the 3's near the ends are touching each other. Fold the tab over to cover the blank triangle on the other side, and glue it to the blank triangle. One side of the hexagon should be all 1's, one side should be all 2's, and all the 3's should hidden.
Photos 1-6 below show the construction of a hexaflexagon made out of cardboard triangles on a backing made from a strip of cloth. It has been decorated in six colors; orange, blue, and red in figure 1 correspond to 1, 2, and 3 in the diagram above. The opposite side, figure 2, is decorated with purple, gray, and yellow. Note the different patterns used for the colors on the two sides. Figure 3 shows the first fold, and figure 4 the result of the first nine folds, which form a spiral. Figures 5-6 show the final folding of the spiral to make a hexagon; in 5, two red faces have been hidden by a valley fold, and in 6, two red faces on the bottom side have been hidden by a mountain fold. After figure 6, the final loose triangle is folded over and attached to the other end of the original strip so that one side is all blue, and the other all orange.

Photos 7 and 8 show the process of everting the hexaflexagon to show the formerly hidden red triangles. By further manipulations, all six colors can be exposed. Faces 1, 2, and 3 are easier to find while faces 4, 5, and 6 are more difficult to find. An easy way to expose all six faces is using the Tuckerman traverse. It's named after Bryant Tuckerman, one of the first to investigate the properties of hexaflexagons. The Tuckerman traverse involves the repeated flexing by pinching one corner and flex from exactly the same corner every time. If the corner refuses to open, move to an adjacent corner and keep flexing. This procedure brings you to a 12-face cycle. During this procedure, however, 1, 2, and 3 show up three times as frequently as 4, 5, and 6. The cycle proceeds as follows:
1-3-6-1-3-2-4-3-2-1-5-2
And then back to 1 again.
Each color/face can also be exposed in more than one way. In figure 6, for example, each blue triangle has at the center its corner decorated with a wedge, but it is also possible, for example, to make the ones decorated with Y's come to the center. There are 18 such possible configurations for triangles with different colors, and they can be seen by flexing the hexahexaflexagon in all possible ways in theory, but only 15 can be flexed by the ordinary hexahexaflexagon. The 3 extra configurations are impossible due to the arrangement of the 4, 5, and 6 tiles at the back flap. (The 60-degree angles in the rhombi formed by the adjacent 4, 5, or 6 tiles will only appear on the sides and never will appear at the center because it would require one to cut the strip, which is topologically forbidden.)
The one shown is not the only hexahexaflexagon. Others can be constructed from different shaped nets of eighteen equilateral triangles. One hexahexaflexagon, constructed from an irregular paper strip, is almost identical to the one shown above, except that all 18 configurations can be flexed on this version.
logo: a regular pentagon
divided from the center into five isosceles triangles, with angles 72-54-54. Because of its fivefold symmetry, the pentaflexagon cannot be folded in half. However, a complex series of flexes results in its transformation from displaying sides 1 and 2 on the front and back, to displaying its previously hidden sides 3 and 4. http://loki3.com/flex/penta.html
By further dividing the 72-54-54 triangles of the pentaflexagon into 36-54-90 right triangles produces one variation of the 10-sided decaflexagon (http://loki3.com/flex/deca.html).
s called pentaflexagons http://delta.cs.cinvestav.mx/~mcintosh/comun/pentags/pentags.html, and from heptagons called heptaflexagons http://delta.cs.cinvestav.mx/~mcintosh/comun/heptagon/heptagon.html. These should be distinguished from the "ordinary" penta- and heptaflexagons described above, which are made out of isosceles triangles, and can be made to lie flat.
Tetraflexagons:
Hexaflexagons:
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, flexagons are flat models, usually constructed by folding strips of paper, that can be flexed or folded in certain ways to reveal faces besides the two that were originally on the back and front.
Flexagons are usually square or rectangular (tetraflexagons) or hexagonal (hexaflexagons). A prefix can be added to the name to indicate the number of faces that the model can display, including the two faces (back and front) that are visible before flexing. For example, a hexaflexagon with a total of six faces is called a hexahexaflexagon.
In hexaflexagon theory (that is, concerning flexagons with six sides), flexagons are usually defined in terms of pats.
Two flexagons are equivalent if one can be transformed to the other by a series of pinches and rotations. Flexagon equivalence is an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
.
Discovery and introduction
The discovery of the first flexagon, a trihexaflexagon, is credited to the British student Arthur H. StoneArthur Harold Stone
Arthur Harold Stone was a British mathematician born in London, who worked mostly in topology. His wife was American mathematician Dorothy Maharam...
who was studying at Princeton University
Princeton University
Princeton University is a private research university located in Princeton, New Jersey, United States. The school is one of the eight universities of the Ivy League, and is one of the nine Colonial Colleges founded before the American Revolution....
in the USA
United States
The United States of America is a federal constitutional republic comprising fifty states and a federal district...
in 1939, allegedly while he was playing with the strips he had cut off his foolscap
Foolscap folio
Foolscap folio is paper cut to the size of 8 1/2 × 13 1/2 in...
paper to convert it to letter size
Letter (paper size)
Letter or US Letter is the most common paper size for office use in several countries, including the United States, Canada, Mexico, Bolivia, Colombia, Venezuela, the Philippines, and Chile. It measures 8.5 by 11 inches ....
. Stone's colleagues Bryant Tuckerman
Bryant Tuckerman
Louis Bryant Tuckerman, III was an American mathematician, born in Lincoln, Nebraska. He was a member of the team that developed the Data Encryption Standard ....
, Richard P. Feynman
Richard Feynman
Richard Phillips Feynman was an American physicist known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics and the physics of the superfluidity of supercooled liquid helium, as well as in particle physics...
and John W. Tukey became interested in the idea and formed the Princeton Flexagon Committee. Tuckerman worked out a topological
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
method, called the Tuckerman traverse, for revealing all the faces of a flexagon.
Flexagons were introduced to the general public by the recreational mathematician
Recreational mathematics
Recreational mathematics is an umbrella term, referring to mathematical puzzles and mathematical games.Not all problems in this field require a knowledge of advanced mathematics, and thus, recreational mathematics often attracts the curiosity of non-mathematicians, and inspires their further study...
Martin Gardner
Martin Gardner
Martin Gardner was an American mathematics and science writer specializing in recreational mathematics, but with interests encompassing micromagic, stage magic, literature , philosophy, scientific skepticism, and religion...
, writing in 1956 in his inaugural "Mathematical Games" column for Scientific American
Scientific American
Scientific American is a popular science magazine. It is notable for its long history of presenting science monthly to an educated but not necessarily scientific public, through its careful attention to the clarity of its text as well as the quality of its specially commissioned color graphics...
magazine.
Attempted commercial development
In 1955, Russell Rogers and Leonard D'Andrea of Homestead Park, PennsylvaniaHomestead, Pennsylvania
Homestead is a borough in Allegheny County, Pennsylvania, USA, in the "Mon Valley," southeast of downtown Pittsburgh and directly across the river from the city limit line. The borough is known for the Homestead Strike of 1892, an important event in the history of labor relations in the United...
applied for, and in 1959 were granted, U.S. Patent #2,883,185 for the hexahexaflexagon, under the title "Changeable Amusement Devices and the Like." The patent imagined possible applications of the device "as a toy, as an advertising display device, or as an educational geometric device." A few such novelties were produced by the Herbick & Held Printing Company
Herbick & Held Printing Company
Herbick & Held Printing Company was a high-end financial printer in Pittsburgh, Pennsylvania, that did business with many prominent companies such as US Steel, Mellon Bank and Gulf Oil, printing annual reports and other financial documents. It also printed many volumes for the University of...
, the Pittsburgh printing firm where Rogers worked. But the device, marketed as the "Hexmo", failed to catch on commercially.
Tritetraflexagon
The tritetraflexagon is the simplest tetraflexagon (flexagon with squareSquare (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
sides). The "tri" in the name means it has three faces, two of which are visible at any given time if the flexagon is pressed flat.
It is folded from a strip of six squares of paper like this:

To fold this shape into a tritetraflexagon, first crease each line between two squares. Then fold the mountain fold away from you and the valley fold towards you, and add a small piece of tape like this

This figure has two faces visible, built of squares marked with "A"s and "B"s. The face of "C"s is hidden inside the flexagon. To reveal it, fold the flexagon flat and then unfold it, like this

The construction of the tritetraflexagon is similar to the mechanism used in the traditional Jacob's Ladder
Jacob's ladder (toy)
A Jacob's ladder is a folk toy consisting of blocks of wood held together by strings or ribbons. When the ladder is held at one end, blocks appear to cascade down the strings. However, this effect is a visual illusion which is the result of one block after another flipping over...
children's toy, in Rubik's Magic
Rubik's Magic
Rubik's Magic, like Rubik's Cube, is a mechanical puzzle invented by the Hungarian sculptor and professor of architecture Ernő Rubik and first manufactured by Matchbox in the mid-1980s....
and in the magic wallet trick or the Himber
Richard Himber
Richard Himber was an American bandleader, composer, violinist, magician and practical joker.-Early life:He was born as Herbert Richard Imber in Newark, New Jersey to the owner of a chain of meat stores...
wallet.
Cyclic hexa-tetraflexagon
A more complicated cyclic hexatetraflexagon doesn't require any gluing. To make it, take a square piece of paper and fold it twice vertically and horizontally to measure it into a 4 by 4 grid. Cut a square hole in the middle by removing 2 by 2 cell area. Make sure all edges are straight. Fold the sides to the middle.Cyclic hexatetraflexagon doesn't have "dead ends" but you can keep folding it until you reach the starting position. If your colour the sides as you go, you can see the states more clearly.
Hexaflexagons
Hexaflexagons come in great variety, distinguished by the number of faces that can be achieved by flexing the assembled figure.Trihexaflexagon
A hexaflexagon with three faces.While this is the simplest of the hexaflexagons to make and to manage, it is a very satisfying place to begin. It is made from a single strip of paper, divided into ten equilateral triangles. Patterns are available at The Flexagon Portal.
It is possible to automatically section and correctly place photographs (or drawings) of your own selection onto Trihexaflexagons using the simple program Foto-TriHexaFlexagon.
Hexahexaflexagon
This hexaflexagon has six faces.
Make a mountain fold between the first 2 and the first 3. Continue folding in a spiral fashion, for a total of nine folds. You now have a straight strip with ten triangles on each side. There are two places where 3's are next to each other; fold in both these places so as to hide the 3's, forming a hexagon with a triangular tab sticking out. Lift one end of the hexagon around the other so that the 3's near the ends are touching each other. Fold the tab over to cover the blank triangle on the other side, and glue it to the blank triangle. One side of the hexagon should be all 1's, one side should be all 2's, and all the 3's should hidden.
Photos 1-6 below show the construction of a hexaflexagon made out of cardboard triangles on a backing made from a strip of cloth. It has been decorated in six colors; orange, blue, and red in figure 1 correspond to 1, 2, and 3 in the diagram above. The opposite side, figure 2, is decorated with purple, gray, and yellow. Note the different patterns used for the colors on the two sides. Figure 3 shows the first fold, and figure 4 the result of the first nine folds, which form a spiral. Figures 5-6 show the final folding of the spiral to make a hexagon; in 5, two red faces have been hidden by a valley fold, and in 6, two red faces on the bottom side have been hidden by a mountain fold. After figure 6, the final loose triangle is folded over and attached to the other end of the original strip so that one side is all blue, and the other all orange.

Photos 7 and 8 show the process of everting the hexaflexagon to show the formerly hidden red triangles. By further manipulations, all six colors can be exposed. Faces 1, 2, and 3 are easier to find while faces 4, 5, and 6 are more difficult to find. An easy way to expose all six faces is using the Tuckerman traverse. It's named after Bryant Tuckerman, one of the first to investigate the properties of hexaflexagons. The Tuckerman traverse involves the repeated flexing by pinching one corner and flex from exactly the same corner every time. If the corner refuses to open, move to an adjacent corner and keep flexing. This procedure brings you to a 12-face cycle. During this procedure, however, 1, 2, and 3 show up three times as frequently as 4, 5, and 6. The cycle proceeds as follows:
1-3-6-1-3-2-4-3-2-1-5-2
And then back to 1 again.
Each color/face can also be exposed in more than one way. In figure 6, for example, each blue triangle has at the center its corner decorated with a wedge, but it is also possible, for example, to make the ones decorated with Y's come to the center. There are 18 such possible configurations for triangles with different colors, and they can be seen by flexing the hexahexaflexagon in all possible ways in theory, but only 15 can be flexed by the ordinary hexahexaflexagon. The 3 extra configurations are impossible due to the arrangement of the 4, 5, and 6 tiles at the back flap. (The 60-degree angles in the rhombi formed by the adjacent 4, 5, or 6 tiles will only appear on the sides and never will appear at the center because it would require one to cut the strip, which is topologically forbidden.)
The one shown is not the only hexahexaflexagon. Others can be constructed from different shaped nets of eighteen equilateral triangles. One hexahexaflexagon, constructed from an irregular paper strip, is almost identical to the one shown above, except that all 18 configurations can be flexed on this version.
Other hexaflexagons
While the most commonly seen hexaflexagons have either three or six faces, variations exist with four, five, and seven faces. Nets for these can be found at the flexagon.net website.Right octaflexagon and right dodecaflexagon
In these more recently discovered flexagons, each square or equilateral triangular face of a conventional flexagon is further divided into two right triangles, permitting additional flexing modes (http://www.eighthsquare.com/12-gon.html). The division of the square faces of tetraflexagons into right isosceles triangles yields the octaflexagons (http://loki3.com/flex/octa.html), and the division of the triangular faces of the hexaflexagons into 30-60-90 right triangles yields the dodecaflexagons (http://loki3.com/flex/dodeca.html).Pentaflexagon and right decaflexagon
In its flat state, the pentaflexagon looks much like the ChryslerChrysler
Chrysler Group LLC is a multinational automaker headquartered in Auburn Hills, Michigan, USA. Chrysler was first organized as the Chrysler Corporation in 1925....
logo: a regular pentagon
Pentagon
In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...
divided from the center into five isosceles triangles, with angles 72-54-54. Because of its fivefold symmetry, the pentaflexagon cannot be folded in half. However, a complex series of flexes results in its transformation from displaying sides 1 and 2 on the front and back, to displaying its previously hidden sides 3 and 4. http://loki3.com/flex/penta.html
By further dividing the 72-54-54 triangles of the pentaflexagon into 36-54-90 right triangles produces one variation of the 10-sided decaflexagon (http://loki3.com/flex/deca.html).
Generalized isosceles n-flexagon
The pentaflexagon (described above) is one of an infinite sequence of flexagons based on dividing a regular n-gon into n isosceles triangles. There is the heptaflexagon (http://loki3.com/flex/hepta.html), the isosceles octaflexagon (http://loki3.com/flex/octa.html#iso), enneaflexagon (http://loki3.com/flex/ennea.html#iso), and on and on...Nonplanar pentaflexagon and nonplanar heptaflexagon
Harold V. McIntosh also describes "nonplanar" (i.e., they can't be flexed so they lie flat) flexagons; ones folded from pentagonPentagon
In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...
s called pentaflexagons http://delta.cs.cinvestav.mx/~mcintosh/comun/pentags/pentags.html, and from heptagons called heptaflexagons http://delta.cs.cinvestav.mx/~mcintosh/comun/heptagon/heptagon.html. These should be distinguished from the "ordinary" penta- and heptaflexagons described above, which are made out of isosceles triangles, and can be made to lie flat.
See also
- Geometric group theoryGeometric group theoryGeometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
- Cayley tree
- OctahedronOctahedronIn geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
: two identically formed nonplanar flexagons: one octahedron
External links
Flexagons:- My Flexagon Experiences by Harold V. McIntosh — contains valuable historical information and theory; the author's site has several flexagon related papers listed in http://delta.cs.cinvestav.mx/~mcintosh/oldweb/pflexagon.html and even boasts some flexagon videoVideoVideo is the technology of electronically capturing, recording, processing, storing, transmitting, and reconstructing a sequence of still images representing scenes in motion.- History :...
s in http://delta.cs.cinvestav.mx/~mcintosh/videos/hexaflexagonos/videosflexa.html. - The Flexagon Portal — Robin Moseley's site has patterns for a large variety of flexagons.
- Flexagons is a good introduction, including a large number of links.
- Flexagons — Scott Sherman's site, with a bewildering array of flexagons of different shapes.
Tetraflexagons:
- MathWorldMathWorldMathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...
's page on tetraflexagons, including three nets - Folding User Interfaces - A mobile phone design concept based on a tetraflexagon; Folding the design gives access to different user interfaces.
- Flexifier - a simple online tetraflexagon generator
- Instructions for making cyclic hexa-tetraflexagon from just one piece of paper.
Hexaflexagons:
- Flexagons — 1962 paper by Antony S. Conrad and Daniel K. Hartline (RIAS)
- MathWorld entry on Hexaflexagons
- Hexaflexagon Toolkit software for printing flexagons from your own pictures
- Hexaflexagons — a catalog compiled by Antonio Carlos M. de Queiroz (c.1973).
Includes a program named HexaFind that finds all the possible Tuckerman traverses for given orders of hexaflexagons.

