Flux limiter
Encyclopedia
Flux limiters are used in high resolution scheme
s – numerical schemes used to solve problems in science and engineering, particularly fluid dynamics
, described by partial differential equations (PDE's). They are used in high resolution schemes, such as the MUSCL scheme
, to avoid the spurious oscillations (wiggles) that would otherwise occur with high order spatial discretisation schemes due to shocks, discontinuities or sharp changes in the solution domain. Use of flux limiters, together with an appropriate high resolution scheme, make the solutions total variation diminishing
(TVD).
Note that flux limiters are also referred to as slope limiters because they both have the same mathematical form, and both have the effect of limiting the solution gradient near shocks or discontinuities. In general, the term flux limiter is used when the limiter acts on system flux
es, and slope limiter is used when the limiter acts on system states.
s for solving problems described by PDEs and only come into operation when sharp wave fronts are present. For smoothly changing waves, the flux limiters do not operate and the spatial derivatives can be represented by higher order approximations without introducing non-real oscillations. Consider the 1D semi-discrete scheme below,
where,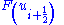
and 
represent edge fluxes for the ith cell. If these edge fluxes can be represented by low and high resolution schemes, then a flux limiter can switch between these schemes depending upon the gradients close to the particular cell, as follows,
,
,
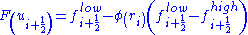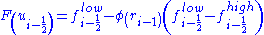where
low resolution flux,
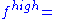high resolution flux,
flux limiter function,
and
represents the ratio of successive gradients on the solution mesh, i.e.,
.
The limiter function is constrained to be greater than or equal to zero, i.e.,
. Therefore, when the limiter is equal to zero (sharp gradient, opposite slopes or zero gradient), the flux is represented by a low resolution scheme. Similarly, when the limiter is equal to 1 (smooth solution), it is represented by a high resolution scheme. The various limiters have differing switching characteristics and are selected according to the particular problem and solution scheme. No particular limiter has been found to work well for all problems, and a particular choice is usually made on a trial and error basis.
:
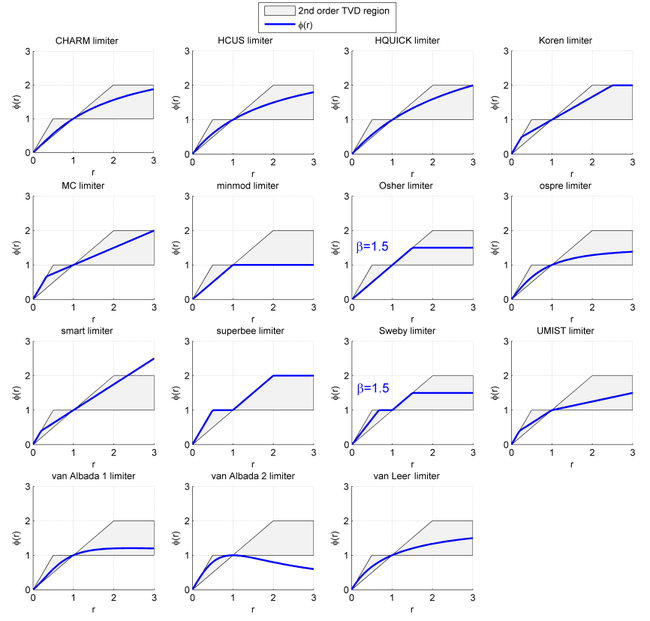
CHARM [not 2nd order TVD] (Zhou, 1995)
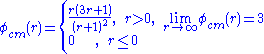
HCUS [not 2nd order TVD] (Waterson & Deconinck, 1995)
.
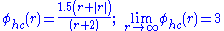HQUICK [not 2nd order TVD] (Waterson & Deconinck, 1995)
.
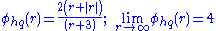Koren (Koren, 1993) – third-order accurate for sufficiently smooth data
.
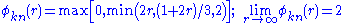minmod – symmetric (Roe
, 1986)
.
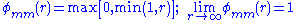monotonized central (MC) – symmetric (van Leer, 1977)
.
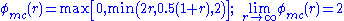Osher (Chatkravathy and Osher
, 1983)
.
ospre – symmetric (Waterson & Deconinck, 1995)
.
smart [not 2nd order TVD] (Gaskell & Lau, 1988)
.
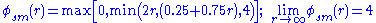superbee – symmetric (Roe, 1986)
.
Sweby – symmetric (Sweby, 1984)
.
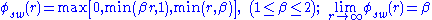UMIST (Lien & Leschziner, 1994)
.
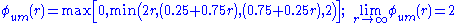van Albada 1 – symmetric (van Albada, et al., 1982)
.
van Albada 2 – alternative form [not 2nd order TVD] used on high spatial order schemes (Kermani, 2003)
.
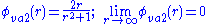van Leer – symmetric (van Leer
, 1974)
.
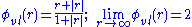All the above limiters indicated as being symmetric, exhibit the following symmetry property,
.
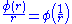This is a desirable property as it ensures that the limiting actions for forward and backward gradients operate in the same way.
Unless indicated to the contrary, the above limiter functions are second order TVD
. This means that they are designed such that they pass through a certain region of the solution, known as the TVD region, in order to guarantee stability of the scheme. Second-order, TVD limiters satisfy at least the following criteria:
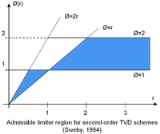
The admissible limiter region for second-order TVD schemes is shown in the Sweby Diagram opposite (Sweby, 1984), and plots showing limiter functions overlaid onto the TVD region are shown below. In this image, plots for the Osher and Sweby limiters have been generated using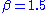
.
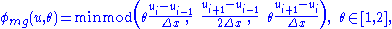
where the multivariable minmod limiter is defined as
Note: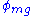
is most dissipative for 
when it reduces to 
and is least dissipative for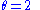 
.
High resolution scheme
High-resolution schemes are used in the numerical solution of partial differential equations where high accuracy is required in the presence of shocks or discontinuities...
s – numerical schemes used to solve problems in science and engineering, particularly fluid dynamics
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
, described by partial differential equations (PDE's). They are used in high resolution schemes, such as the MUSCL scheme
MUSCL scheme
In the study of partial differential equations, the MUSCL scheme is a finite volume method that can provide highly accurate numerical solutions for a given system, even in cases where the solutions exhibit shocks, discontinuities, or large gradients...
, to avoid the spurious oscillations (wiggles) that would otherwise occur with high order spatial discretisation schemes due to shocks, discontinuities or sharp changes in the solution domain. Use of flux limiters, together with an appropriate high resolution scheme, make the solutions total variation diminishing
Total variation diminishing
In numerical methods, total variation diminishing is a property of certain discretization schemes used to solve hyperbolic partial differential equations...
(TVD).
Note that flux limiters are also referred to as slope limiters because they both have the same mathematical form, and both have the effect of limiting the solution gradient near shocks or discontinuities. In general, the term flux limiter is used when the limiter acts on system flux
Flux
In the various subfields of physics, there exist two common usages of the term flux, both with rigorous mathematical frameworks.* In the study of transport phenomena , flux is defined as flow per unit area, where flow is the movement of some quantity per time...
es, and slope limiter is used when the limiter acts on system states.
How they work
The main idea behind the construction of flux limiter schemes is to limit the spatial derivatives to realistic values – for scientific and engineering problems this usually means physically realisable values. They are used in high resolution schemeHigh resolution scheme
High-resolution schemes are used in the numerical solution of partial differential equations where high accuracy is required in the presence of shocks or discontinuities...
s for solving problems described by PDEs and only come into operation when sharp wave fronts are present. For smoothly changing waves, the flux limiters do not operate and the spatial derivatives can be represented by higher order approximations without introducing non-real oscillations. Consider the 1D semi-discrete scheme below,
where,
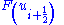and represent edge fluxes for the ith cell. If these edge fluxes can be represented by low and high resolution schemes, then a flux limiter can switch between these schemes depending upon the gradients close to the particular cell, as follows,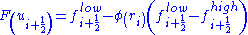,,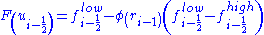where
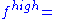low resolution flux, high resolution flux, flux limiter function,and
represents the ratio of successive gradients on the solution mesh, i.e.,.The limiter function is constrained to be greater than or equal to zero, i.e.,
. Therefore, when the limiter is equal to zero (sharp gradient, opposite slopes or zero gradient), the flux is represented by a low resolution scheme. Similarly, when the limiter is equal to 1 (smooth solution), it is represented by a high resolution scheme. The various limiters have differing switching characteristics and are selected according to the particular problem and solution scheme. No particular limiter has been found to work well for all problems, and a particular choice is usually made on a trial and error basis.Limiter functions
The following are common forms of flux/slope limiter function,:CHARM [not 2nd order TVD] (Zhou, 1995)
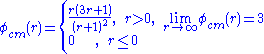
HCUS [not 2nd order TVD] (Waterson & Deconinck, 1995)
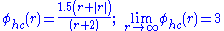.HQUICK [not 2nd order TVD] (Waterson & Deconinck, 1995)
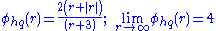.Koren (Koren, 1993) – third-order accurate for sufficiently smooth data
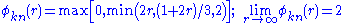.minmod – symmetric (Roe
Philip L. Roe
Philip L. Roe is a Professor of Aerospace Engineering at the University of Michigan in Ann Arbor. He is known for his work in the field of Computational Fluid Dynamics and Magnetohydrodynamics. Roe made fundamental contributions to the development of high-resolution schemes for hyperbolic...
, 1986)
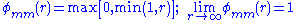.monotonized central (MC) – symmetric (van Leer, 1977)
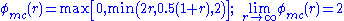.Osher (Chatkravathy and Osher
Stanley Osher
Stanley Osher is an American mathematician, known for his many contributions in shock capturing, level set methods, and PDE-based methods in computer vision and image processing...
, 1983)
.ospre – symmetric (Waterson & Deconinck, 1995)
.smart [not 2nd order TVD] (Gaskell & Lau, 1988)
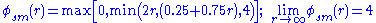.superbee – symmetric (Roe, 1986)
.Sweby – symmetric (Sweby, 1984)
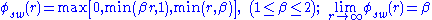.UMIST (Lien & Leschziner, 1994)
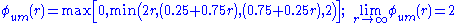.van Albada 1 – symmetric (van Albada, et al., 1982)
.van Albada 2 – alternative form [not 2nd order TVD] used on high spatial order schemes (Kermani, 2003)
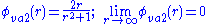.van Leer – symmetric (van Leer
Bram van Leer
Bram van Leer is the Arthur B. Modine Professor of aerospace engineering at the University of Michigan, in Ann Arbor. He specialises in Computational fluid dynamics , fluid dynamics, and numerical analysis where he has made substantial contributions.-Research work:Professor van Leer developed...
, 1974)
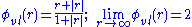.All the above limiters indicated as being symmetric, exhibit the following symmetry property,
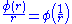.This is a desirable property as it ensures that the limiting actions for forward and backward gradients operate in the same way.
Total variation diminishing
In numerical methods, total variation diminishing is a property of certain discretization schemes used to solve hyperbolic partial differential equations...
. This means that they are designed such that they pass through a certain region of the solution, known as the TVD region, in order to guarantee stability of the scheme. Second-order, TVD limiters satisfy at least the following criteria:
,
,
,
,
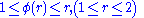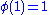The admissible limiter region for second-order TVD schemes is shown in the Sweby Diagram opposite (Sweby, 1984), and plots showing limiter functions overlaid onto the TVD region are shown below. In this image, plots for the Osher and Sweby limiters have been generated using
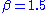.Generalised minmod limiter
An additional limiter that has an interesting form is the van-Leer's one-parameter family of minmod limiters (van Leer, 1979; Harten and Osher, 1987; Kurganov and Tadmor, 2000). It is defined as follows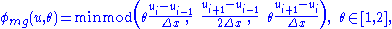where the multivariable minmod limiter is defined as
Note:
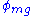is most dissipative for when it reduces to and is least dissipative for 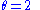.See also
- Godunov's theoremGodunov's theoremIn numerical analysis and computational fluid dynamics, Godunov's theorem — also known as Godunov's order barrier theorem — is a mathematical theorem important in the development of the theory of high resolution schemes for the numerical solution of partial differential equations.The theorem states...
- High resolution schemeHigh resolution schemeHigh-resolution schemes are used in the numerical solution of partial differential equations where high accuracy is required in the presence of shocks or discontinuities...
- MUSCL schemeMUSCL schemeIn the study of partial differential equations, the MUSCL scheme is a finite volume method that can provide highly accurate numerical solutions for a given system, even in cases where the solutions exhibit shocks, discontinuities, or large gradients...
- Sergei K. GodunovSergei K. GodunovSergei Konstantinovich Godunov is professor at the Sobolev Institute of Mathematics of the Russian Academy of Sciences in Novosibirsk, Russia....
- Total variation diminishingTotal variation diminishingIn numerical methods, total variation diminishing is a property of certain discretization schemes used to solve hyperbolic partial differential equations...