
Total variation diminishing
Encyclopedia
In numerical methods, total variation diminishing (TVD) is a property of certain discretization
schemes used to solve hyperbolic partial differential equation
s. The concept of TVD was introduced by Ami Harten
.
In systems described by partial differential equation
s, such as the following hyperbolic advection equation,

the total variation
(TV) is given by,
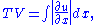
and the total variation
for the discrete case is,
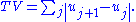
A numerical method is said to be total variation diminishing (TVD) if,
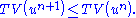
A system is said to be monotonicity preserving if the following properties are maintained as a function of t:
proved the following properties for a numerical scheme,
Monotone schemes are attractive for solving engineering and scientific problems because they do not provide non-physical solutions.
Godunov's theorem
proves that only first order linear schemes preserve monotonicity and are therefore TVD. Higher order linear schemes, although more accurate for smooth solutions, are not TVD and tend to introduce spurious oscillations (wiggles) where discontinuities or shocks arise. To overcome these drawbacks, various high-resolution, non-linear techniques have been developed, often using flux/slope limiter
s.
Discretization
In mathematics, discretization concerns the process of transferring continuous models and equations into discrete counterparts. This process is usually carried out as a first step toward making them suitable for numerical evaluation and implementation on digital computers...
schemes used to solve hyperbolic partial differential equation
Hyperbolic partial differential equation
In mathematics, a hyperbolic partial differential equation of order n is a partial differential equation that, roughly speaking, has a well-posed initial value problem for the first n−1 derivatives. More precisely, the Cauchy problem can be locally solved for arbitrary initial data along...
s. The concept of TVD was introduced by Ami Harten
Ami Harten
Amiram Harten was an American/Israeli applied mathematician. Harten made fundamental contribution to the development of high-resolution schemes for the solution of hyperbolic partial differential equations...
.
In systems described by partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s, such as the following hyperbolic advection equation,

the total variation
Total variation
In mathematics, the total variation identifies several slightly different concepts, related to the structure of the codomain of a function or a measure...
(TV) is given by,
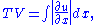
and the total variation
Total variation
In mathematics, the total variation identifies several slightly different concepts, related to the structure of the codomain of a function or a measure...
for the discrete case is,
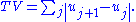
A numerical method is said to be total variation diminishing (TVD) if,
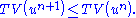
A system is said to be monotonicity preserving if the following properties are maintained as a function of t:
- No new local extrema can be created within the solution spatial domain,
- The value of a local minimum is non-decreasing, and the value of a local maximum is non-increasing.
proved the following properties for a numerical scheme,
- A monotone scheme is TVD, and
- A TVD scheme is monotonicityMonotonic functionIn mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
preserving.
Monotone schemes are attractive for solving engineering and scientific problems because they do not provide non-physical solutions.
Godunov's theorem
Godunov's theorem
In numerical analysis and computational fluid dynamics, Godunov's theorem — also known as Godunov's order barrier theorem — is a mathematical theorem important in the development of the theory of high resolution schemes for the numerical solution of partial differential equations.The theorem states...
proves that only first order linear schemes preserve monotonicity and are therefore TVD. Higher order linear schemes, although more accurate for smooth solutions, are not TVD and tend to introduce spurious oscillations (wiggles) where discontinuities or shocks arise. To overcome these drawbacks, various high-resolution, non-linear techniques have been developed, often using flux/slope limiter
Flux limiter
Flux limiters are used in high resolution schemes – numerical schemes used to solve problems in science and engineering, particularly fluid dynamics, described by partial differential equations...
s.
See also
- Flux limiters
- Godunov's theoremGodunov's theoremIn numerical analysis and computational fluid dynamics, Godunov's theorem — also known as Godunov's order barrier theorem — is a mathematical theorem important in the development of the theory of high resolution schemes for the numerical solution of partial differential equations.The theorem states...
- High-resolution scheme
- MUSCL schemeMUSCL schemeIn the study of partial differential equations, the MUSCL scheme is a finite volume method that can provide highly accurate numerical solutions for a given system, even in cases where the solutions exhibit shocks, discontinuities, or large gradients...
- Sergei K. GodunovSergei K. GodunovSergei Konstantinovich Godunov is professor at the Sobolev Institute of Mathematics of the Russian Academy of Sciences in Novosibirsk, Russia....
- Total variationTotal variationIn mathematics, the total variation identifies several slightly different concepts, related to the structure of the codomain of a function or a measure...
Further reading
- Hirsch, C. (1990), Numerical Computation of Internal and External Flows, Vol 2, Wiley.
- Laney, C. B. (1998), Computational Gas Dynamics, Cambridge University Press.
- Toro, E. F. (1999), Riemann Solvers and Numerical Methods for Fluid Dynamics, Springer-Verlag.
- Tannehill, J. C., Anderson, D. A.Dale A. AndersonDale A. Anderson is an American aerospace engineer and computational fluid dynamicist. Anderson was the Professor of Aerospace Engineering and Vice President for Research and Dean of Graduate Students at the University of Texas at Arlington, United States...
, and Pletcher, R. H. (1997), Computational Fluid Mechanics and Heat Transfer, 2nd Ed., Taylor & Francis. - Wesseling, P. (2001), Principles of Computational Fluid Dynamics, Springer-Verlag.

