Fock matrix
Encyclopedia
In the Hartree-Fock method of quantum mechanics
, the Fock matrix is a matrix approximating the single-electron energy operator of a given quantum
system in a given set of basis
vectors.
It is most often formed in computational chemistry
when attempting to solve the Roothaan equations
for an atomic or molecular system. The Fock matrix is actually an approximation to the true Hamiltonian operator of the quantum system. It includes the effects of electron-electron
repulsion only in an average way. Importantly, because the Fock operator is a one-electron operator, it does not include the electron correlation energy.
The Fock matrix is defined by the Fock operator. For the restricted case which assumes closed-shell orbitals and single-determinantal wavefunctions, the Fock operator for the i-th electron is given by:
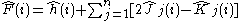
where:
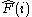
is the Fock operator for the i-th electron in the system,
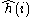
is the one-electron hamiltonian for the i-th electron,
is the total number of occupied orbitals in the system (equal to
, where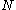
is the number of electrons),
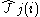
is the Coulomb operator
, defining the repulsive force between the j-th and i-th electrons in the system,
is the exchange operator
, defining the quantistic effect produced by exchanging two electrons.
For systems with unpaired electrons there are many choices of Fock matrices.
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, the Fock matrix is a matrix approximating the single-electron energy operator of a given quantum
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
system in a given set of basis
Basis set
Basis set can refer to:* Basis * Basis set...
vectors.
It is most often formed in computational chemistry
Computational chemistry
Computational chemistry is a branch of chemistry that uses principles of computer science to assist in solving chemical problems. It uses the results of theoretical chemistry, incorporated into efficient computer programs, to calculate the structures and properties of molecules and solids...
when attempting to solve the Roothaan equations
Roothaan equations
The Roothaan equations are a representation of the Hartree-Fock equation in a non orthonormal basis set which can be of Gaussian-type or Slater-type. It applies to closed-shell molecules or atoms where all molecular orbitals or atomic orbitals, respectively, are doubly occupied. This is generally...
for an atomic or molecular system. The Fock matrix is actually an approximation to the true Hamiltonian operator of the quantum system. It includes the effects of electron-electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
repulsion only in an average way. Importantly, because the Fock operator is a one-electron operator, it does not include the electron correlation energy.
The Fock matrix is defined by the Fock operator. For the restricted case which assumes closed-shell orbitals and single-determinantal wavefunctions, the Fock operator for the i-th electron is given by:
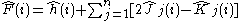
where:
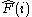
is the Fock operator for the i-th electron in the system,
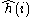
is the one-electron hamiltonian for the i-th electron,
is the total number of occupied orbitals in the system (equal to
Floor function
In mathematics and computer science, the floor and ceiling functions map a real number to the largest previous or the smallest following integer, respectively...
, where
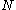is the number of electrons),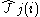is the Coulomb operator
Coulomb operator
The Coulomb operator, named after Charles-Augustin de Coulomb, is a quantum mechanical operator used in the field of quantum chemistry. Specifically, it is a term found in the Fock operator...
, defining the repulsive force between the j-th and i-th electrons in the system,
is the exchange operator
Exchange operator
The Exchange operator is a quantum mechanical operator used in the field of quantum chemistry. Specifically, it is a term found in the Fock operator...
, defining the quantistic effect produced by exchanging two electrons.
For systems with unpaired electrons there are many choices of Fock matrices.
See also
- Hartree-FockHartree-FockIn computational physics and chemistry, the Hartree–Fock method is an approximate method for the determination of the ground-state wave function and ground-state energy of a quantum many-body system....
- Unrestricted Hartree–Fock
- Restricted open-shell Hartree–Fock