Hartree-Fock
Encyclopedia
In computational physics
and chemistry
, the Hartree–Fock (HF) method is an approximate method for the determination of the ground-state
wave function and ground-state
energy of a quantum many-body system
.
The Hartree–Fock method assumes that the exact, N-body wave function of the system can be approximated by a single Slater determinant
(in the case where the particles are fermion
s) or by a single permanent
(in the case of boson
s) of N spin-orbitals. By invoking the variational principle
, one can derive a set of N-coupled equations for the N spin orbitals. Solution of these equations yields the Hartree–Fock wave function and energy of the system, which are approximations of the exact ones.
The Hartree–Fock method finds its typical application in the solution of the electronic Schrödinger equation
of atoms, molecules, and solids but it has also found widespread use in nuclear physics
. (See Hartree–Fock–Bogolyubov for a discussion of its application in nuclear structure theory.) The rest of this article will focus on applications in electronic structure theory.
The Hartree–Fock method is also called, especially in the older literature, the self-consistent field method (SCF). The solutions to the resulting non-linear equations behave as if each particle is subjected to the mean field created by all other particles (see the Fock operator below). The equations are almost universally solved by means of an iterative
, fixed-point type algorithm (see the following section for more details). This solution scheme is not the only one possible and is not an essential feature of the Hartree–Fock method.
For molecules, Hartree–Fock is the central starting point for most ab initio quantum chemistry methods
.
The discussion here is only for the Restricted Hartree–Fock method, where the atom or molecule is a closed-shell system with all orbitals (atomic or molecular) are doubly occupied. Open-shell
systems, where some of the electrons are not paired, can be dealt with by one of two Hartree–Fock methods:
in 1926. In 1927 D. R. Hartree
introduced a procedure, which he called the self-consistent field method, to calculate approximate wave functions and energies for atoms and ions. Hartree was guided by some earlier, semi-empirical methods of the early 1920s (by E. Fues, R. B. Lindsay
, and himself) set in the old quantum theory
of Bohr.
In the Bohr model
of the atom, the energy of a state with principal quantum number
n is given in atomic units as . It was observed from atomic spectra that the energy levels of many-electron atoms are well described by applying a modified version of Bohr's formula. By introducing the quantum defect
. It was observed from atomic spectra that the energy levels of many-electron atoms are well described by applying a modified version of Bohr's formula. By introducing the quantum defect
d as an empirical parameter, the energy levels of a generic atom was well approximated by the formula , in the sense that one could reproduce fairly well the observed transitions levels observed in the X-ray
, in the sense that one could reproduce fairly well the observed transitions levels observed in the X-ray
region (for example, see the empirical discussion and derivation in Moseley's law
). The existence of a non-zero quantum defect was attributed to electron-electron repulsion, which clearly does not exist in the isolated hydrogen atom. This repulsion resulted in partial screening
of the bare nuclear charge. These early researchers later introduced other potentials containing additional empirical parameters with the hope of better reproducing the experimental data.
Hartree sought to do away with empirical parameters and solve the many-body time-independent Schrödinger equation from fundamental physical principles, i.e., ab initio
. His first proposed method of solution became known as the Hartree method. However, many of Hartree's contemporaries did not understand the physical reasoning behind the Hartree method: it appeared to many people to contain empirical elements, and its connection to the solution of the many-body Schrödinger equation was unclear. However, in 1928 J. C. Slater
and J. A. Gaunt independently showed that the Hartree method could be couched on a sounder theoretical basis by applying the variational principle
to an ansatz
(trial wave function) as a product of single-particle functions.
In 1930 Slater and V. A. Fock
independently pointed out that the Hartree method did not respect the principle of antisymmetry
of the wave function. The Hartree method used the Pauli exclusion principle
in its older formulation, forbidding the presence of two electrons in the same quantum state. However, this was shown to be fundamentally incomplete in its neglect of quantum statistics.
It was then shown that a Slater determinant
, a determinant
of one-particle orbitals first used by Heisenberg and Dirac in 1926, trivially satisfies the antisymmetric
property of the exact solution and hence is a suitable ansatz
for applying the variational principle
. The original Hartree method can then be viewed as an approximation to the Hartree–Fock method by neglecting exchange
. Fock's original method relied heavily on group theory
and was too abstract for contemporary physicists to understand and implement. In 1935 Hartree reformulated the method more suitably for the purposes of calculation.
The Hartree–Fock method, despite its physically more accurate picture, was little used until the advent of electronic computers in the 1950s due to the much greater computational demands over the early Hartree method and empirical models. Initially, both the Hartree method and the Hartree–Fock method were applied exclusively to atoms, where the spherical symmetry of the system allowed one to greatly simplify the problem. These approximate methods were (and are) often used together with the central field approximation
, to impose that electrons in the same shell have the same radial part, and to restrict the variational solution to be a spin eigenfunction. Even so, solution by hand of the Hartree–Fock equations for a medium sized atom were laborious; small molecules required computational resources far beyond what was available before 1950.
and the diatomic hydrogen cation being notable one-electron exceptions), the problem is solved numerically. Due to the nonlinearities introduced by the Hartree–Fock approximation, the equations are solved using a nonlinear method such as iteration
, which gives rise to the name "self-consistent field method."
Relaxation of the last two approximations give rise to many so-called post-Hartree–Fock methods.

states that for a time-independent Hamiltonian operator, any trial wave function will have an energy expectation value that is greater than or equal to the true ground state
wave function corresponding to the given Hamiltonian. Because of this, the Hartree–Fock energy is an upper bound to the true ground state energy of a given molecule. In the context of the Hartree–Fock method, the best possible solution is at the Hartree–Fock limit; i.e., the limit of the Hartree–Fock energy as the basis set approaches completeness
. (The other is the full-CI limit, where the last two approximations of the Hartree–Fock theory as described above are completely undone. It is only when both limits are attained that the exact solution, up to the Born–Oppenheimer approximation, is obtained.) The Hartree–Fock energy is the minimal energy for a single Slater determinant.
The starting point for the Hartree–Fock method is a set of approximate one-electron wave functions known as spin-orbitals. For an atomic orbital
calculation, these are typically the orbitals for a hydrogenic atom (an atom with only one electron, but the appropriate nuclear charge). For a molecular orbital
or crystalline calculation, the initial approximate one-electron wave functions are typically a linear combination of atomic orbitals (LCAO).
The orbitals above only account for the presence of other electrons in an average manner. In the Hartree–Fock method, the effect of other electrons are accounted for in a mean-field theory context. The orbitals are optimized by requiring them to minimize the energy of the respective Slater determinant. The resultant variational conditions on the orbitals lead to a new one-electron operator, the Fock operator. At the minimum, the occupied orbitals are eigensolutions to the Fock operator via a unitary transformation
between themselves. The Fock operator is an effective one-electron Hamiltonian operator being the sum of two terms. The first is a sum of kinetic energy operators for each electron, the internuclear repulsion energy, and a sum of nuclear-electronic Coulombic
attraction terms. The second are Coulombic repulsion terms between electrons in a mean-field theory description; a net repulsion energy for each electron in the system, which is calculated by treating all of the other electrons within the molecule as a smooth distribution of negative charge. This is the major simplification inherent in the Hartree–Fock method, and is equivalent to the fifth simplification in the above list.
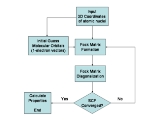
Since the Fock operator depends on the orbitals used to construct the corresponding Fock matrix
, the eigenfunctions of the Fock operator are in turn new orbitals which can be used to construct a new Fock operator. In this way, the Hartree–Fock orbitals are optimized iteratively until the change in total electronic energy falls below a predefined threshold. In this way, a set of self-consistent one-electron orbitals are calculated. The Hartree–Fock electronic wave function is then the Slater determinant constructed out of these orbitals. Following the basic postulates of quantum mechanics, the Hartree–Fock wave function can then be used to compute any desired chemical or physical property within the framework of the Hartree–Fock method and the approximations employed.
where
is the one-electron Fock operator generated by the orbitals ,
,
is the one-electron core Hamiltonian
,
is the Coulomb operator
, defining the electron-electron repulsion energy due to the orbital of the jth electron,
is the exchange operator
, defining the electron exchange energy. Finding the Hartree–Fock one-electron wave functions is now equivalent to solving the eigenfunction equation:
where are a set of one-electron wave functions, called the Hartree–Fock molecular orbitals.
are a set of one-electron wave functions, called the Hartree–Fock molecular orbitals.
Typically, in modern Hartree–Fock calculations, the one-electron wave functions are approximated by a linear combination of atomic orbitals. These atomic orbitals are called Slater-type orbital
s. Furthermore, it is very common for the "atomic orbitals" in use to actually be composed of a linear combination of one or more Gaussian-type orbitals
, rather than Slater-type orbitals, in the interests of saving large amounts of computation time.
Various basis sets
are used in practice, most of which are composed of Gaussian functions. In some applications, an orthogonalization method such as the Gram–Schmidt process is performed in order to produce a set of orthogonal basis functions. This can in principle save computational time when the computer is solving the Roothaan–Hall equations
by converting the overlap matrix
effectively to an identity matrix
. However, in most modern computer programs for molecular Hartree–Fock calculations this procedure is not followed due to the high numerical cost of orthogonalization and the advent of more efficient, often sparse, algorithms for solving the generalized eigenvalue problem, of which the Roothaan–Hall equations
are an example.
can be a problem with this procedure and there are various ways of combating this instability. One of the most basic and generally applicable is called F-mixing or damping. With F-mixing, once a single electron wave function is calculated it is not used directly. Instead, some combination of that calculated wave function and the previous wave functions for that electron is used—the most common being a simple linear combination of the calculated and immediately preceding wave function. A clever dodge, employed by Hartree, for atomic calculations was to increase the nuclear charge, thus pulling all the electrons closer together. As the system stabilised, this was gradually reduced to the correct charge. In molecular calculations a similar approach is sometimes used by first calculating the wave function for a positive ion and then to use these orbitals as the starting point for the neutral molecule. Modern molecular Hartree–Fock computer programs use a variety of methods to ensure convergence of the Roothaan–Hall equations.
of the Fock operator. Others expand the true multi-electron wave function in terms of a linear combination of Slater determinants—such as multi-configurational self-consistent field
, configuration interaction
, quadratic configuration interaction
, and complete active space SCF (CASSCF). Still others (such as variational quantum Monte Carlo
) modify the Hartree–Fock wave function by multiplying it by a correlation function ("Jastrow" factor), a term which is explicitly a function of multiple electrons that cannot be decomposed into independent single-particle functions.
An alternative to Hartree–Fock calculations used in some cases is density functional theory
, which treats both exchange and correlation energies, albeit approximately. Indeed, it is common to use calculations that are a hybrid of the two methods—the popular B3LYP scheme is one such hybrid functional
method.
Another option is to use modern valence bond methods.
Concepts
People
Computational physics
Computational physics is the study and implementation of numerical algorithms to solve problems in physics for which a quantitative theory already exists...
and chemistry
Computational chemistry
Computational chemistry is a branch of chemistry that uses principles of computer science to assist in solving chemical problems. It uses the results of theoretical chemistry, incorporated into efficient computer programs, to calculate the structures and properties of molecules and solids...
, the Hartree–Fock (HF) method is an approximate method for the determination of the ground-state
Stationary state
In quantum mechanics, a stationary state is an eigenvector of the Hamiltonian, implying the probability density associated with the wavefunction is independent of time . This corresponds to a quantum state with a single definite energy...
wave function and ground-state
Stationary state
In quantum mechanics, a stationary state is an eigenvector of the Hamiltonian, implying the probability density associated with the wavefunction is independent of time . This corresponds to a quantum state with a single definite energy...
energy of a quantum many-body system
Many-body problem
The many-body problem is a general name for a vast category of physical problems pertaining to the properties of microscopic systems made of a large number of interacting particles. Microscopic here implies that quantum mechanics has to be used to provide an accurate description of the system...
.
The Hartree–Fock method assumes that the exact, N-body wave function of the system can be approximated by a single Slater determinant
Slater determinant
In quantum mechanics, a Slater determinant is an expression that describes the wavefunction of a multi-fermionic system that satisfies anti-symmetry requirements and consequently the Pauli exclusion principle by changing sign upon exchange of fermions . It is named for its discoverer, John C...
(in the case where the particles are fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s) or by a single permanent
Permanent
The permanent of a square matrix in linear algebra, is a function of the matrix similar to the determinant. The permanent, as well as the determinant, is a polynomial in the entries of the matrix...
(in the case of boson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
s) of N spin-orbitals. By invoking the variational principle
Variational principle
A variational principle is a scientific principle used within the calculus of variations, which develops general methods for finding functions which minimize or maximize the value of quantities that depend upon those functions...
, one can derive a set of N-coupled equations for the N spin orbitals. Solution of these equations yields the Hartree–Fock wave function and energy of the system, which are approximations of the exact ones.
The Hartree–Fock method finds its typical application in the solution of the electronic Schrödinger equation
Molecular Hamiltonian
In atomic, molecular, and optical physics as well as in quantum chemistry, molecular Hamiltonian is the name given to the Hamiltonian representing the energy of the electrons and nuclei in a molecule...
of atoms, molecules, and solids but it has also found widespread use in nuclear physics
Nuclear physics
Nuclear physics is the field of physics that studies the building blocks and interactions of atomic nuclei. The most commonly known applications of nuclear physics are nuclear power generation and nuclear weapons technology, but the research has provided application in many fields, including those...
. (See Hartree–Fock–Bogolyubov for a discussion of its application in nuclear structure theory.) The rest of this article will focus on applications in electronic structure theory.
The Hartree–Fock method is also called, especially in the older literature, the self-consistent field method (SCF). The solutions to the resulting non-linear equations behave as if each particle is subjected to the mean field created by all other particles (see the Fock operator below). The equations are almost universally solved by means of an iterative
Iterative method
In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...
, fixed-point type algorithm (see the following section for more details). This solution scheme is not the only one possible and is not an essential feature of the Hartree–Fock method.
For molecules, Hartree–Fock is the central starting point for most ab initio quantum chemistry methods
Ab initio quantum chemistry methods
Ab initio quantum chemistry methods are computational chemistry methods based on quantum chemistry. The term ab initiowas first used in quantum chemistry by Robert Parr and coworkers, including David Craig in a semiempirical study on the excited states of benzene.The background is described by Parr...
.
The discussion here is only for the Restricted Hartree–Fock method, where the atom or molecule is a closed-shell system with all orbitals (atomic or molecular) are doubly occupied. Open-shell
Open shell
In the context of atomic orbitals, an open shell is a valence shell which is not completely filled with electrons or that has not given all of its valence electrons through chemical bonds with other atoms or molecules during a chemical reaction. Atoms generally reach a noble gas configuration in a...
systems, where some of the electrons are not paired, can be dealt with by one of two Hartree–Fock methods:
- Restricted open-shell Hartree–Fock (ROHF)
- Unrestricted Hartree–Fock (UHF)
Brief history
The origin of the Hartree–Fock method dates back to the end of the 1920s, soon after the derivation of the Schrödinger equationSchrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
in 1926. In 1927 D. R. Hartree
Douglas Hartree
Douglas Rayner Hartree PhD, FRS was an English mathematician and physicist most famous for the development of numerical analysis and its application to the Hartree-Fock equations of atomic physics and the construction of the meccano differential analyser.-Early life:Douglas Hartree was born in...
introduced a procedure, which he called the self-consistent field method, to calculate approximate wave functions and energies for atoms and ions. Hartree was guided by some earlier, semi-empirical methods of the early 1920s (by E. Fues, R. B. Lindsay
Robert Bruce Lindsay
Robert Bruce Lindsay was an American physicist and physics professor, known for his prolific authorship of physics books in acoustics, and historical and philosophical analyses of physics.-Biography:...
, and himself) set in the old quantum theory
Old quantum theory
The old quantum theory was a collection of results from the years 1900–1925 which predate modern quantum mechanics. The theory was never complete or self-consistent, but was a collection of heuristic prescriptions which are now understood to be the first quantum corrections to classical mechanics...
of Bohr.
In the Bohr model
Bohr model
In atomic physics, the Bohr model, introduced by Niels Bohr in 1913, depicts the atom as a small, positively charged nucleus surrounded by electrons that travel in circular orbits around the nucleus—similar in structure to the solar system, but with electrostatic forces providing attraction,...
of the atom, the energy of a state with principal quantum number
Principal quantum number
In atomic physics, the principal quantum symbolized as n is the firstof a set of quantum numbers of an atomic orbital. The principal quantum number can only have positive integer values...
n is given in atomic units as
 . It was observed from atomic spectra that the energy levels of many-electron atoms are well described by applying a modified version of Bohr's formula. By introducing the quantum defect
. It was observed from atomic spectra that the energy levels of many-electron atoms are well described by applying a modified version of Bohr's formula. By introducing the quantum defectQuantum defect
The term quantum defect is ambiguous. Various meanings are discussed below. Characteristic is that the defect deals with the loss on the smallest energy scale of light: that of the quantum.-Quantum defect in laser science:...
d as an empirical parameter, the energy levels of a generic atom was well approximated by the formula
 , in the sense that one could reproduce fairly well the observed transitions levels observed in the X-ray
, in the sense that one could reproduce fairly well the observed transitions levels observed in the X-rayX-ray
X-radiation is a form of electromagnetic radiation. X-rays have a wavelength in the range of 0.01 to 10 nanometers, corresponding to frequencies in the range 30 petahertz to 30 exahertz and energies in the range 120 eV to 120 keV. They are shorter in wavelength than UV rays and longer than gamma...
region (for example, see the empirical discussion and derivation in Moseley's law
Moseley's law
Moseley's law is an empirical law concerning the characteristic x-rays that are emitted by atoms. The law was discovered and published by the English physicist Henry Moseley in 1913...
). The existence of a non-zero quantum defect was attributed to electron-electron repulsion, which clearly does not exist in the isolated hydrogen atom. This repulsion resulted in partial screening
Screening effect
In solids, especially in metals and semiconductors, the electrostatic screening or screening effect reduces the electrostatic field and Coulomb potential of an ion inside the solid...
of the bare nuclear charge. These early researchers later introduced other potentials containing additional empirical parameters with the hope of better reproducing the experimental data.
Hartree sought to do away with empirical parameters and solve the many-body time-independent Schrödinger equation from fundamental physical principles, i.e., ab initio
Ab initio quantum chemistry methods
Ab initio quantum chemistry methods are computational chemistry methods based on quantum chemistry. The term ab initiowas first used in quantum chemistry by Robert Parr and coworkers, including David Craig in a semiempirical study on the excited states of benzene.The background is described by Parr...
. His first proposed method of solution became known as the Hartree method. However, many of Hartree's contemporaries did not understand the physical reasoning behind the Hartree method: it appeared to many people to contain empirical elements, and its connection to the solution of the many-body Schrödinger equation was unclear. However, in 1928 J. C. Slater
John C. Slater
John Clarke Slater was a noted American physicist who made major contributions to the theory of the electronic structure of atoms, molecules and solids. This work is of ongoing importance in chemistry, as well as in many areas of physics. He also made major contributions to microwave electronics....
and J. A. Gaunt independently showed that the Hartree method could be couched on a sounder theoretical basis by applying the variational principle
Variational principle
A variational principle is a scientific principle used within the calculus of variations, which develops general methods for finding functions which minimize or maximize the value of quantities that depend upon those functions...
to an ansatz
Ansatz
Ansatz is a German noun with several meanings in the English language.It is widely encountered in physics and mathematics literature.Since ansatz is a noun, in German texts the initial a of this word is always capitalised.-Definition:...
(trial wave function) as a product of single-particle functions.
In 1930 Slater and V. A. Fock
Vladimir Fock
Vladimir Aleksandrovich Fock was a Soviet physicist, who did foundational work on quantum mechanics and quantum electrodynamics....
independently pointed out that the Hartree method did not respect the principle of antisymmetry
Exchange symmetry
Exchange symmetry is derived from a fundamental postulate of quantum statistics, which states that no observable physical quantity should change after exchanging two identical particles...
of the wave function. The Hartree method used the Pauli exclusion principle
Pauli exclusion principle
The Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...
in its older formulation, forbidding the presence of two electrons in the same quantum state. However, this was shown to be fundamentally incomplete in its neglect of quantum statistics.
It was then shown that a Slater determinant
Slater determinant
In quantum mechanics, a Slater determinant is an expression that describes the wavefunction of a multi-fermionic system that satisfies anti-symmetry requirements and consequently the Pauli exclusion principle by changing sign upon exchange of fermions . It is named for its discoverer, John C...
, a determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of one-particle orbitals first used by Heisenberg and Dirac in 1926, trivially satisfies the antisymmetric
Exchange symmetry
Exchange symmetry is derived from a fundamental postulate of quantum statistics, which states that no observable physical quantity should change after exchanging two identical particles...
property of the exact solution and hence is a suitable ansatz
Ansatz
Ansatz is a German noun with several meanings in the English language.It is widely encountered in physics and mathematics literature.Since ansatz is a noun, in German texts the initial a of this word is always capitalised.-Definition:...
for applying the variational principle
Variational principle
A variational principle is a scientific principle used within the calculus of variations, which develops general methods for finding functions which minimize or maximize the value of quantities that depend upon those functions...
. The original Hartree method can then be viewed as an approximation to the Hartree–Fock method by neglecting exchange
Exchange symmetry
Exchange symmetry is derived from a fundamental postulate of quantum statistics, which states that no observable physical quantity should change after exchanging two identical particles...
. Fock's original method relied heavily on group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
and was too abstract for contemporary physicists to understand and implement. In 1935 Hartree reformulated the method more suitably for the purposes of calculation.
The Hartree–Fock method, despite its physically more accurate picture, was little used until the advent of electronic computers in the 1950s due to the much greater computational demands over the early Hartree method and empirical models. Initially, both the Hartree method and the Hartree–Fock method were applied exclusively to atoms, where the spherical symmetry of the system allowed one to greatly simplify the problem. These approximate methods were (and are) often used together with the central field approximation
Central field approximation
In atomic physics, the central field approximation for many-electron atoms takes the combined electric fields of the nucleus and all the electrons acting on any of the electrons to be radial and to be the same for all the electrons in the atom...
, to impose that electrons in the same shell have the same radial part, and to restrict the variational solution to be a spin eigenfunction. Even so, solution by hand of the Hartree–Fock equations for a medium sized atom were laborious; small molecules required computational resources far beyond what was available before 1950.
Hartree–Fock algorithm
The Hartree–Fock method is typically used to solve the time-independent Schrödinger equation for a multi-electron atom or molecule as described in the Born–Oppenheimer approximation. Since there are no known solutions for many-electron systems (hydrogenic atomsHydrogen atom
A hydrogen atom is an atom of the chemical element hydrogen. The electrically neutral atom contains a single positively-charged proton and a single negatively-charged electron bound to the nucleus by the Coulomb force...
and the diatomic hydrogen cation being notable one-electron exceptions), the problem is solved numerically. Due to the nonlinearities introduced by the Hartree–Fock approximation, the equations are solved using a nonlinear method such as iteration
Iteration
Iteration means the act of repeating a process usually with the aim of approaching a desired goal or target or result. Each repetition of the process is also called an "iteration," and the results of one iteration are used as the starting point for the next iteration.-Mathematics:Iteration in...
, which gives rise to the name "self-consistent field method."
Approximations
The Hartree–Fock method makes five major simplifications in order to deal with this task:- The Born–Oppenheimer approximation is inherently assumed. The full molecular wave function is actually a function of the coordinates of each of the nuclei, in addition to those of the electrons.
- Typically, relativisticSpecial relativitySpecial relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
effects are completely neglected. The momentum operatorMomentumIn classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
is assumed to be completely non-relativistic. - The variational solution is assumed to be a linear combinationLinear combinationIn mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of a finite number of basis functionsBasis set (chemistry)A basis set in chemistry is a set of functions used to create the molecular orbitals, which are expanded as a linear combination of such functions with the weights or coefficients to be determined. Usually these functions are atomic orbitals, in that they are centered on atoms. Otherwise, the...
, which are usually (but not always) chosen to be orthogonal. The finite basis set is assumed to be approximately completeCompletenessIn general, an object is complete if nothing needs to be added to it. This notion is made more specific in various fields.-Logical completeness:In logic, semantic completeness is the converse of soundness for formal systems...
. - Each energy eigenfunction is assumed to be describable by a single Slater determinantSlater determinantIn quantum mechanics, a Slater determinant is an expression that describes the wavefunction of a multi-fermionic system that satisfies anti-symmetry requirements and consequently the Pauli exclusion principle by changing sign upon exchange of fermions . It is named for its discoverer, John C...
, an antisymmetrized product of one-electron wave functions (i.e., orbitals). - The mean field approximationMean field theoryMean field theory is a method to analyse physical systems with multiple bodies. A many-body system with interactions is generally very difficult to solve exactly, except for extremely simple cases . The n-body system is replaced by a 1-body problem with a chosen good external field...
is implied. Effects arising from deviations from this assumption, known as electron correlation, are completely neglected for the electrons of opposite spin, but are taken into account for electrons of parallel spin. (Electron correlation should not be confused with electron exchange, which is fully accounted for in the Hartree–Fock method.)
Relaxation of the last two approximations give rise to many so-called post-Hartree–Fock methods.

Variational optimization of orbitals
The variational theoremVariational method (quantum mechanics)
In quantum mechanics, the variational method is one way of finding approximations to the lowest energy eigenstate or ground state, and some excited states...
states that for a time-independent Hamiltonian operator, any trial wave function will have an energy expectation value that is greater than or equal to the true ground state
Ground state
The ground state of a quantum mechanical system is its lowest-energy state; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state...
wave function corresponding to the given Hamiltonian. Because of this, the Hartree–Fock energy is an upper bound to the true ground state energy of a given molecule. In the context of the Hartree–Fock method, the best possible solution is at the Hartree–Fock limit; i.e., the limit of the Hartree–Fock energy as the basis set approaches completeness
Completeness
In general, an object is complete if nothing needs to be added to it. This notion is made more specific in various fields.-Logical completeness:In logic, semantic completeness is the converse of soundness for formal systems...
. (The other is the full-CI limit, where the last two approximations of the Hartree–Fock theory as described above are completely undone. It is only when both limits are attained that the exact solution, up to the Born–Oppenheimer approximation, is obtained.) The Hartree–Fock energy is the minimal energy for a single Slater determinant.
The starting point for the Hartree–Fock method is a set of approximate one-electron wave functions known as spin-orbitals. For an atomic orbital
Atomic orbital
An atomic orbital is a mathematical function that describes the wave-like behavior of either one electron or a pair of electrons in an atom. This function can be used to calculate the probability of finding any electron of an atom in any specific region around the atom's nucleus...
calculation, these are typically the orbitals for a hydrogenic atom (an atom with only one electron, but the appropriate nuclear charge). For a molecular orbital
Molecular orbital
In chemistry, a molecular orbital is a mathematical function describing the wave-like behavior of an electron in a molecule. This function can be used to calculate chemical and physical properties such as the probability of finding an electron in any specific region. The term "orbital" was first...
or crystalline calculation, the initial approximate one-electron wave functions are typically a linear combination of atomic orbitals (LCAO).
The orbitals above only account for the presence of other electrons in an average manner. In the Hartree–Fock method, the effect of other electrons are accounted for in a mean-field theory context. The orbitals are optimized by requiring them to minimize the energy of the respective Slater determinant. The resultant variational conditions on the orbitals lead to a new one-electron operator, the Fock operator. At the minimum, the occupied orbitals are eigensolutions to the Fock operator via a unitary transformation
Unitary transformation
In mathematics, a unitary transformation may be informally defined as a transformation that respects the inner product: the inner product of two vectors before the transformation is equal to their inner product after the transformation....
between themselves. The Fock operator is an effective one-electron Hamiltonian operator being the sum of two terms. The first is a sum of kinetic energy operators for each electron, the internuclear repulsion energy, and a sum of nuclear-electronic Coulombic
Coulomb's law
Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
attraction terms. The second are Coulombic repulsion terms between electrons in a mean-field theory description; a net repulsion energy for each electron in the system, which is calculated by treating all of the other electrons within the molecule as a smooth distribution of negative charge. This is the major simplification inherent in the Hartree–Fock method, and is equivalent to the fifth simplification in the above list.
Since the Fock operator depends on the orbitals used to construct the corresponding Fock matrix
Fock matrix
In the Hartree-Fock method of quantum mechanics, the Fock matrix is a matrix approximating the single-electron energy operator of a given quantum system in a given set of basis vectors....
, the eigenfunctions of the Fock operator are in turn new orbitals which can be used to construct a new Fock operator. In this way, the Hartree–Fock orbitals are optimized iteratively until the change in total electronic energy falls below a predefined threshold. In this way, a set of self-consistent one-electron orbitals are calculated. The Hartree–Fock electronic wave function is then the Slater determinant constructed out of these orbitals. Following the basic postulates of quantum mechanics, the Hartree–Fock wave function can then be used to compute any desired chemical or physical property within the framework of the Hartree–Fock method and the approximations employed.
The Fock operator
Because the electron-electron repulsion term of the electronic molecular Hamiltonian involves the coordinates of two different electrons, it is necessary to reformulate it in an approximate way. Under this approximation, (outlined under Hartree–Fock algorithm), all of the terms of the exact Hamiltonian except the nuclear-nuclear repulsion term are re-expressed as the sum of one-electron operators outlined below. The "(1)" following each operator symbol simply indicates that the operator is 1-electron in nature.where
is the one-electron Fock operator generated by the orbitals
 ,
,is the one-electron core Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
,
is the Coulomb operator
Coulomb operator
The Coulomb operator, named after Charles-Augustin de Coulomb, is a quantum mechanical operator used in the field of quantum chemistry. Specifically, it is a term found in the Fock operator...
, defining the electron-electron repulsion energy due to the orbital of the jth electron,
is the exchange operator
Exchange operator
The Exchange operator is a quantum mechanical operator used in the field of quantum chemistry. Specifically, it is a term found in the Fock operator...
, defining the electron exchange energy. Finding the Hartree–Fock one-electron wave functions is now equivalent to solving the eigenfunction equation:
where
 are a set of one-electron wave functions, called the Hartree–Fock molecular orbitals.
are a set of one-electron wave functions, called the Hartree–Fock molecular orbitals.Linear combination of atomic orbitals
- Main article: basis setBasis set (chemistry)A basis set in chemistry is a set of functions used to create the molecular orbitals, which are expanded as a linear combination of such functions with the weights or coefficients to be determined. Usually these functions are atomic orbitals, in that they are centered on atoms. Otherwise, the...
Typically, in modern Hartree–Fock calculations, the one-electron wave functions are approximated by a linear combination of atomic orbitals. These atomic orbitals are called Slater-type orbital
Slater-type orbital
Slater-type orbitals are functions used as atomic orbitals in the linear combination of atomic orbitals molecular orbital method. They are named after the physicist John C. Slater, who introduced them in 1930....
s. Furthermore, it is very common for the "atomic orbitals" in use to actually be composed of a linear combination of one or more Gaussian-type orbitals
Gaussian orbital
In computational chemistry and molecular physics, Gaussian orbitals are functions used as atomic orbitals in the LCAO method for the computation of electron orbitals in molecules and numerous properties that depend on these.- Rationale :The principal reason for the use of Gaussian basis functions...
, rather than Slater-type orbitals, in the interests of saving large amounts of computation time.
Various basis sets
Basis set (chemistry)
A basis set in chemistry is a set of functions used to create the molecular orbitals, which are expanded as a linear combination of such functions with the weights or coefficients to be determined. Usually these functions are atomic orbitals, in that they are centered on atoms. Otherwise, the...
are used in practice, most of which are composed of Gaussian functions. In some applications, an orthogonalization method such as the Gram–Schmidt process is performed in order to produce a set of orthogonal basis functions. This can in principle save computational time when the computer is solving the Roothaan–Hall equations
Roothaan equations
The Roothaan equations are a representation of the Hartree-Fock equation in a non orthonormal basis set which can be of Gaussian-type or Slater-type. It applies to closed-shell molecules or atoms where all molecular orbitals or atomic orbitals, respectively, are doubly occupied. This is generally...
by converting the overlap matrix
Overlap matrix
The overlap matrix is a square matrix, used in quantum chemistry to describe the inter-relationship of a set of basis vectors of a quantum system. In particular, if the vectors are orthogonal to one another, the overlap matrix will be diagonal. In addition, if the basis vectors form an...
effectively to an identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
. However, in most modern computer programs for molecular Hartree–Fock calculations this procedure is not followed due to the high numerical cost of orthogonalization and the advent of more efficient, often sparse, algorithms for solving the generalized eigenvalue problem, of which the Roothaan–Hall equations
Roothaan equations
The Roothaan equations are a representation of the Hartree-Fock equation in a non orthonormal basis set which can be of Gaussian-type or Slater-type. It applies to closed-shell molecules or atoms where all molecular orbitals or atomic orbitals, respectively, are doubly occupied. This is generally...
are an example.
Numerical stability
Numerical stabilityNumerical stability
In the mathematical subfield of numerical analysis, numerical stability is a desirable property of numerical algorithms. The precise definition of stability depends on the context, but it is related to the accuracy of the algorithm....
can be a problem with this procedure and there are various ways of combating this instability. One of the most basic and generally applicable is called F-mixing or damping. With F-mixing, once a single electron wave function is calculated it is not used directly. Instead, some combination of that calculated wave function and the previous wave functions for that electron is used—the most common being a simple linear combination of the calculated and immediately preceding wave function. A clever dodge, employed by Hartree, for atomic calculations was to increase the nuclear charge, thus pulling all the electrons closer together. As the system stabilised, this was gradually reduced to the correct charge. In molecular calculations a similar approach is sometimes used by first calculating the wave function for a positive ion and then to use these orbitals as the starting point for the neutral molecule. Modern molecular Hartree–Fock computer programs use a variety of methods to ensure convergence of the Roothaan–Hall equations.
Weaknesses, extensions, and alternatives
Of the five simplifications outlined in the section "Hartree–Fock algorithm", the fifth is typically the most important. Neglecting electron correlation can lead to large deviations from experimental results. A number of approaches to this weakness, collectively called post-Hartree–Fock methods, have been devised to include electron correlation to the multi-electron wave function. One of these approaches, Møller–Plesset perturbation theory, treats correlation as a perturbationPerturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
of the Fock operator. Others expand the true multi-electron wave function in terms of a linear combination of Slater determinants—such as multi-configurational self-consistent field
Multi-configurational self-consistent field
Multi-configurational self-consistent field is a method in quantum chemistry used to generate qualitatively correct reference states of molecules in cases where Hartree–Fock and density functional theory are not adequate...
, configuration interaction
Configuration interaction
Configuration interaction is a post-Hartree–Fock linear variational method for solving the nonrelativistic Schrödinger equation within the Born–Oppenheimer approximation for a quantum chemical multi-electron system. Mathematically, configuration simply describes the linear combination...
, quadratic configuration interaction
Quadratic configuration interaction
Quadratic configuration interaction is an extension of Configuration interaction that corrects for size-consistency errors in the all singles and double excitation CI methods ....
, and complete active space SCF (CASSCF). Still others (such as variational quantum Monte Carlo
Variational Monte Carlo
In mathematical physics, variational Monte Carlo is a quantum Monte Carlo method that applies the variational method to approximate the ground state of the system.The expectation value necessary can be written in the x representation as...
) modify the Hartree–Fock wave function by multiplying it by a correlation function ("Jastrow" factor), a term which is explicitly a function of multiple electrons that cannot be decomposed into independent single-particle functions.
An alternative to Hartree–Fock calculations used in some cases is density functional theory
Density functional theory
Density functional theory is a quantum mechanical modelling method used in physics and chemistry to investigate the electronic structure of many-body systems, in particular atoms, molecules, and the condensed phases. With this theory, the properties of a many-electron system can be determined by...
, which treats both exchange and correlation energies, albeit approximately. Indeed, it is common to use calculations that are a hybrid of the two methods—the popular B3LYP scheme is one such hybrid functional
Hybrid functional
Hybrid functionals are a class of approximations to the exchange-correlation energy functional in density functional theory that incorporate a portion of exact exchange from Hartree-Fock theory with exchange and correlation from other sources...
method.
Another option is to use modern valence bond methods.
Software packages
For a list of software packages known to handle Hartree–Fock calculations, particularly for molecules and solids, see the list of quantum chemistry and solid state physics software.See also
Related fields- Quantum chemistryQuantum chemistryQuantum chemistry is a branch of chemistry whose primary focus is the application of quantum mechanics in physical models and experiments of chemical systems...
- Computational chemistryComputational chemistryComputational chemistry is a branch of chemistry that uses principles of computer science to assist in solving chemical problems. It uses the results of theoretical chemistry, incorporated into efficient computer programs, to calculate the structures and properties of molecules and solids...
- Computational physicsComputational physicsComputational physics is the study and implementation of numerical algorithms to solve problems in physics for which a quantitative theory already exists...
- Quantum chemistry computer programsQuantum chemistry computer programsQuantum chemistry computer programs are used in computational chemistry to implement the methods of quantum chemistry. Most include the Hartree–Fock and some post-Hartree–Fock methods. They may also include density functional theory , molecular mechanics or semi-empirical quantum...
Concepts
- Born–Oppenheimer approximation
- Roothaan equationsRoothaan equationsThe Roothaan equations are a representation of the Hartree-Fock equation in a non orthonormal basis set which can be of Gaussian-type or Slater-type. It applies to closed-shell molecules or atoms where all molecular orbitals or atomic orbitals, respectively, are doubly occupied. This is generally...
- Koopmans' theoremKoopmans' theoremKoopmans' theorem states that in closed-shell Hartree-Fock theory, the first ionization energy of a molecular system is equal to the negative of the orbital energy of the highest occupied molecular orbital...
- Post-Hartree–Fock
- Direct Inversion of Iterative SubspaceDIISDIIS , also known as Pulay mixing, is an extrapolation technique...
People
- Douglas HartreeDouglas HartreeDouglas Rayner Hartree PhD, FRS was an English mathematician and physicist most famous for the development of numerical analysis and its application to the Hartree-Fock equations of atomic physics and the construction of the meccano differential analyser.-Early life:Douglas Hartree was born in...
- Vladimir Aleksandrovich Fock
- Clemens RoothaanClemens C. J. RoothaanClemens C.J. Roothaan was born in 1918 in Nijmegen, the Netherlands. He enrolled TU Delft in 1935 to study electrical engineering. During World War II he was first detained as a prisoner of war camp, later he was sent for a year to a concentration camp in Vught...
- George G. HallGeorge G. HallGeorge Garfield Hall , is an applied mathematician and scientist of distinction, known for original work and contributions to the field of Quantum chemistry....
- John PopleJohn PopleSir John Anthony Pople, KBE, FRS, was a Nobel-Prize winning theoretical chemist. Born in Burnham-on-Sea, Somerset, England, he attended Bristol Grammar School. He won a scholarship to Trinity College, Cambridge in 1943. He received his B. A. in 1946. Between 1945 and 1947 he worked at the Bristol...
- Reinhart AhlrichsReinhart AhlrichsProf. Dr. Reinhart Ahlrichs is a German theoretical chemist.-Biography:Ahlrichs was born on the 16 January 1940 in Göttingen. He studied Physics at the University of Göttingen and received his PhD in 1968 with W. A. Bingel. From 1968-69 he was assistant at Göttingen with Werner Kutzelnigg and from...







