Focus recovery based on the linear canonical transform
Encyclopedia
Focus recovery from a defocused image is an ill-posed problem since it loses the component of high frequency. Most of the methods for focus recovery are based on depth estimation theory. The Linear canonical transform (LCT) gives a scalable kernel to fit many famous optical effects. Using LCTs to approximate an optical system for imaging and inverting this system, theoretically permits recovery of a defocused image.
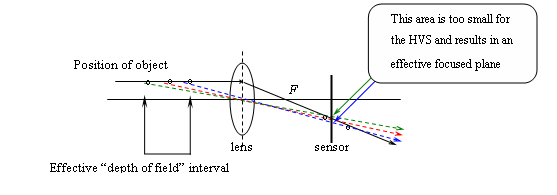In photography, depth of field
(DOF) means an effective focal length. It is usually used for stressing an object and deemphasizing the background (and/or the foreground). The important measure related to DOF is the lens aperture
. Decreasing the diameter of aperture increases focus and lowers resolution and vice versa.
The Huygens-Fresnel principle
describes diffraction
of wave propagation between two fields. It belongs to Fourier optics
rather than geometric optics.The disturbance of diffraction depends on two circumstance parameters, the size of aperture and the interfield distance.
Consider a source field and a destination field, field 1 and field 0, respectively. P1(x1,y1) is the position in the source field, P0(x0,y0) is the position in the destination field. The Huygens-Fresnel principle gives the diffraction formula for two fields U(x0,y0), U(x1,y1) as following:
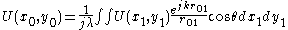
where θ denotes the angle between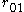
and 
. Replace cosθ by 
and 
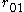by
we get
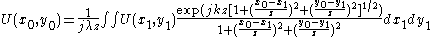
The further distance z or the smaller aperture (x1,y1) causes a greater diffraction. A larger DOF can lead to a more effective focused wave distribution. This seems to be a conflict. Here are the notations:
In conclusion, we can give a summary that diffraction explains a micro behavior whereas DOF shows a macro behavior. Both of them are related to aperture size.
transform and the fractional Fourier transform
. It can be easily controlled by its four parameters, a, b, c, d (3 degrees of freedom). The definition:
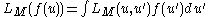
where
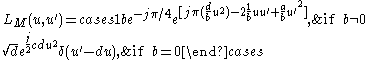
Consider a general imaging system with object distance z0, focal length
of the thin lens
f and an imaging distance z1. The effect of the propagation in freespace acts as nearly a chirp
convolution
, that is, the formula of diffraction. Besides, the effect of the propagation in thin lens acts as a chirp multiplication. The parameters are all simplified as paraxial approximation
s while meeting the freespace propagation. It does not consider aperture size.
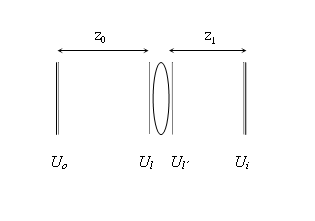
From the properties of the LCT, we can get those 4 parameters for this optical system as:
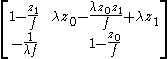
Once the values of z1, z0 and f are known, the LCT can simulate any optical system.
Depth of field and perceptual focus
Depth of field
In optics, particularly as it relates to film and photography, depth of field is the distance between the nearest and farthest objects in a scene that appear acceptably sharp in an image...
(DOF) means an effective focal length. It is usually used for stressing an object and deemphasizing the background (and/or the foreground). The important measure related to DOF is the lens aperture
Aperture
In optics, an aperture is a hole or an opening through which light travels. More specifically, the aperture of an optical system is the opening that determines the cone angle of a bundle of rays that come to a focus in the image plane. The aperture determines how collimated the admitted rays are,...
. Decreasing the diameter of aperture increases focus and lowers resolution and vice versa.
The Huygens-Fresnel principle and DOF
Huygens-Fresnel principle
The Huygens–Fresnel principle is a method of analysis applied to problems of wave propagation both in the far-field limit and in near-field diffraction.-History:...
describes diffraction
Diffraction
Diffraction refers to various phenomena which occur when a wave encounters an obstacle. Italian scientist Francesco Maria Grimaldi coined the word "diffraction" and was the first to record accurate observations of the phenomenon in 1665...
of wave propagation between two fields. It belongs to Fourier optics
Fourier optics
Fourier optics is the study of classical optics using Fourier transforms and can be seen as the dual of the Huygens-Fresnel principle. In the latter case, the wave is regarded as a superposition of expanding spherical waves which radiate outward from actual current sources via a Green's function...
rather than geometric optics.The disturbance of diffraction depends on two circumstance parameters, the size of aperture and the interfield distance.
Consider a source field and a destination field, field 1 and field 0, respectively. P1(x1,y1) is the position in the source field, P0(x0,y0) is the position in the destination field. The Huygens-Fresnel principle gives the diffraction formula for two fields U(x0,y0), U(x1,y1) as following:
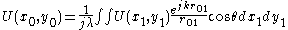
where θ denotes the angle between
and . Replace cosθ by and by we get
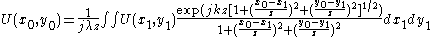
The further distance z or the smaller aperture (x1,y1) causes a greater diffraction. A larger DOF can lead to a more effective focused wave distribution. This seems to be a conflict. Here are the notations:
- Diffraction
- In a real imaging environment, the depths of objects comparing to the aperture are usually not enough to lead to serious diffraction.
- However, a long enough depth of the object can truly blurs the image.
- Effective Focus
- Small aperture, small blurring radius, few wave information.
- Loses details in comparing to a large aperture.
In conclusion, we can give a summary that diffraction explains a micro behavior whereas DOF shows a macro behavior. Both of them are related to aperture size.
Linear canonical transform
As the meaning of “canonical”, the linear canonical transform (LCT) is a scalable transform that connects to lots of important kernels such as the Fresnel transform, FraunhoferFraunhofer
Fraunhofer, , may refer to:*Joseph von Fraunhofer , German physicist*Fraunhofer , a lunar crater*Fraunhofer Society , a large German research organization with 59 institutes throughout Germany...
transform and the fractional Fourier transform
Fractional Fourier transform
In mathematics, in the area of harmonic analysis, the fractional Fourier transform is a linear transformation generalizing the Fourier transform. It can be thought of as the Fourier transform to the n-th power where n need not be an integer — thus, it can transform a function to an...
. It can be easily controlled by its four parameters, a, b, c, d (3 degrees of freedom). The definition:
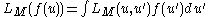
where
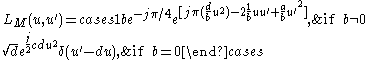
Consider a general imaging system with object distance z0, focal length
Focal length
The focal length of an optical system is a measure of how strongly the system converges or diverges light. For an optical system in air, it is the distance over which initially collimated rays are brought to a focus...
of the thin lens
Thin lens
[Image:Lens1.svg|thumb|A lens can be considered a thin lens if d [Image:Lens1.svg|thumb|A lens can be considered a thin lens if d [Image:Lens1.svg|thumb|A lens can be considered a thin lens if d...
f and an imaging distance z1. The effect of the propagation in freespace acts as nearly a chirp
Chirp
A chirp is a signal in which the frequency increases or decreases with time. In some sources, the term chirp is used interchangeably with sweep signal. It is commonly used in sonar and radar, but has other applications, such as in spread spectrum communications...
convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
, that is, the formula of diffraction. Besides, the effect of the propagation in thin lens acts as a chirp multiplication. The parameters are all simplified as paraxial approximation
Paraxial approximation
In geometric optics, the paraxial approximation is a small-angle approximation used in Gaussian optics and ray tracing of light through an optical system ....
s while meeting the freespace propagation. It does not consider aperture size.
From the properties of the LCT, we can get those 4 parameters for this optical system as:
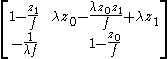
Once the values of z1, z0 and f are known, the LCT can simulate any optical system.