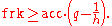Forking lemma
Encyclopedia
The forking lemma is any of a number of related lemmas
in cryptography
research. The lemma states that if an adversary (typically a probabilistic Turing machine
), on inputs drawn from some distribution
, produces an output that has some property with non-negligible probability
, then with non-negligible probability, if the adversary is re-run on new inputs but with the same random tape, its second output will also have the property.
This concept was first used by David Pointcheval and Jacques Stern
in "Security proofs for signature schemes," published in the proceedings of Eurocrypt
1996. In their paper, the forking lemma is specified in terms of an adversary that attacks a digital signature
scheme instantiated in the random oracle
model. They show that if an adversary can forge a signature with non-negligible probability, then there is a non-negligible probability that the same adversary with the same random tape can create a second forgery in an attack with a different random oracle. The forking lemma was later generalized by Mihir Bellare
and Gregory Neven. The forking lemma has been used to prove the security of a variety of digital signature schemes and other random-oracle based cryptographic constructions.
We can then define a "forking algorithm" FA that proceeds as follows, on input x:
Let frk be the probability that FA outputs a triple starting with 1, given an input x chosen randomly from IG. Then
" at a certain point, when some but not all of the input has been examined. In the alternate version, the remaining inputs are re-generated but are generated in the normal way. The point at which the process forks may be something we only want to decide later, possibly based on the behavior of A the first time around: this is why the lemma statement chooses the branching point (J) based on the output of A. The requirement that hJ ≠ h'J is a technical one required by many uses of the lemma. (Note that since both hJ and h'J are chosen randomly from H, then if h is large, which would be normal, the probability of the two values not being distinct is extremely small.)
scheme in the random oracle
model. Then x would be the public parameters (including the public key) A is attacking, and hi would be the output of the random oracle on its ith distinct input. The forking lemma is of use when it would be possible, given two different random signatures of the same message, to solve some underlying hard problem. An adversary that forges once, however, gives rise to one that forges twice on the same message with non-negligible probability through the forking lemma. When A attempts to forge on a message m, we consider the output of A to be (J, y) where y is the forgery, and J is such that m was the Jth unique query to the random oracle (it may be assumed that A will query m at some point, if A is to be successful with non-negligible probability). (If A outputs an incorrect forgery, we consider the output to be (0, y).)
By the forking lemma, the probability (frk) of obtaining two good forgeries y and y' on the same message but with different random oracle outputs (that is, with hJ ≠ h'J) is non-negligible when acc is also non-negligible. This allows us to prove that if the underlying hard problem is indeed hard, then no adversary can forge signatures.
This is the essence of the proof given by Pointcheval and Stern for a modified ElGamal signature scheme
against an adaptive adversary.
provided an attack on blind Schnorr signatures schemes, which were argued to be secure by Pointcheval and Stern. Schnorr also suggested enhancements for securing blind signatures schemes based on discrete logarithm
problem.
Lemma (mathematics)
In mathematics, a lemma is a proven proposition which is used as a stepping stone to a larger result rather than as a statement in-and-of itself...
in cryptography
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
research. The lemma states that if an adversary (typically a probabilistic Turing machine
Probabilistic Turing machine
In computability theory, a probabilistic Turing machine is a non-deterministic Turing machine which randomly chooses between the available transitions at each point according to some probability distribution....
), on inputs drawn from some distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
, produces an output that has some property with non-negligible probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
, then with non-negligible probability, if the adversary is re-run on new inputs but with the same random tape, its second output will also have the property.
This concept was first used by David Pointcheval and Jacques Stern
Jacques Stern
Jacques Stern is a cryptographer, currently a professor at the École Normale Supérieure, where he is Director of the Computer Science Laboratory. He received the 2006 CNRS Gold Medal...
in "Security proofs for signature schemes," published in the proceedings of Eurocrypt
Eurocrypt
Eurocrypt is a conference for cryptography research. The full name of the conference is currently the Annual International Conference on the Theory and Applications of Cryptographic Techniques, but this has not always been its name...
1996. In their paper, the forking lemma is specified in terms of an adversary that attacks a digital signature
Digital signature
A digital signature or digital signature scheme is a mathematical scheme for demonstrating the authenticity of a digital message or document. A valid digital signature gives a recipient reason to believe that the message was created by a known sender, and that it was not altered in transit...
scheme instantiated in the random oracle
Random oracle
In cryptography, a random oracle is an oracle that responds to every query with a random response chosen uniformly from its output domain, except that for any specific query, it responds the same way every time it receives that query...
model. They show that if an adversary can forge a signature with non-negligible probability, then there is a non-negligible probability that the same adversary with the same random tape can create a second forgery in an attack with a different random oracle. The forking lemma was later generalized by Mihir Bellare
Mihir Bellare
Mihir Bellare is a cryptographer and professor at the University of California, San Diego. He has published several seminal papers in the field of cryptography , many coauthored with Phillip Rogaway. Bellare has published a number of papers in the field of Format-Preserving Encryption...
and Gregory Neven. The forking lemma has been used to prove the security of a variety of digital signature schemes and other random-oracle based cryptographic constructions.
Statement of the lemma
The generalized version of the lemma is stated as follows. Let A be a probabilistic algorithm, with inputs (x, h1, ..., hq; r) that outputs a pair (J, y), where r refers to the random tape of A (that is, the random choices A will make). Suppose further that IG is a probability distribution from which x is drawn, and that H is a set of size h from which each of the hi values are drawn according to the uniform distribution. Let acc be the probability that on inputs distributed as described, the J output by A is greater than or equal to 1.We can then define a "forking algorithm" FA that proceeds as follows, on input x:
- Pick a random tape r for A.
- Pick h1, ..., hq uniformly from H.
- Run A on input (x, h1, ..., hq; r) to produce (J, y).
- If J = 0, then return (0, 0, 0).
- Pick h'J, ..., h'q uniformly from H.
- Run A on input (x, h1, ..., hJ−1, h
' J, ..., h' q; r) to produce (J' , y' ). - If J' = J and hJ ≠ h'J then return (1, y, y
' ), otherwise, return (0, 0, 0).
Let frk be the probability that FA outputs a triple starting with 1, given an input x chosen randomly from IG. Then
Intuition
The idea here is to think of A as running two times in related executions, where the process "forksFork (software development)
In software engineering, a project fork happens when developers take a legal copy of source code from one software package and start independent development on it, creating a distinct piece of software...
" at a certain point, when some but not all of the input has been examined. In the alternate version, the remaining inputs are re-generated but are generated in the normal way. The point at which the process forks may be something we only want to decide later, possibly based on the behavior of A the first time around: this is why the lemma statement chooses the branching point (J) based on the output of A. The requirement that hJ ≠ h'J is a technical one required by many uses of the lemma. (Note that since both hJ and h'J are chosen randomly from H, then if h is large, which would be normal, the probability of the two values not being distinct is extremely small.)
Example
For example, let A be an algorithm for breaking a digital signatureDigital signature
A digital signature or digital signature scheme is a mathematical scheme for demonstrating the authenticity of a digital message or document. A valid digital signature gives a recipient reason to believe that the message was created by a known sender, and that it was not altered in transit...
scheme in the random oracle
Random oracle
In cryptography, a random oracle is an oracle that responds to every query with a random response chosen uniformly from its output domain, except that for any specific query, it responds the same way every time it receives that query...
model. Then x would be the public parameters (including the public key) A is attacking, and hi would be the output of the random oracle on its ith distinct input. The forking lemma is of use when it would be possible, given two different random signatures of the same message, to solve some underlying hard problem. An adversary that forges once, however, gives rise to one that forges twice on the same message with non-negligible probability through the forking lemma. When A attempts to forge on a message m, we consider the output of A to be (J, y) where y is the forgery, and J is such that m was the Jth unique query to the random oracle (it may be assumed that A will query m at some point, if A is to be successful with non-negligible probability). (If A outputs an incorrect forgery, we consider the output to be (0, y).)
By the forking lemma, the probability (frk) of obtaining two good forgeries y and y' on the same message but with different random oracle outputs (that is, with hJ ≠ h'J) is non-negligible when acc is also non-negligible. This allows us to prove that if the underlying hard problem is indeed hard, then no adversary can forge signatures.
This is the essence of the proof given by Pointcheval and Stern for a modified ElGamal signature scheme
ElGamal signature scheme
The ElGamal signature scheme is a digital signature scheme which is based on the difficulty of computing discrete logarithms. It was described by Taher ElGamal in 1984....
against an adaptive adversary.
Known issues with application of forking lemma
The reduction provided by the forking lemma is not a tight reduction. Pointcheval and Stern proposed security arguments for Digital Signatures and Blind Signature using Forking Lemma. Claus P. SchnorrClaus P. Schnorr
Claus-Peter Schnorr is a distinguished German mathematician and cryptographer. He received his Ph.D. from the University of Saarbrücken in 1966, and his habilitation in 1970. Schnorr's contributions to cryptography include his study of Schnorr groups, which are used in the digital signature...
provided an attack on blind Schnorr signatures schemes, which were argued to be secure by Pointcheval and Stern. Schnorr also suggested enhancements for securing blind signatures schemes based on discrete logarithm
Discrete logarithm
In mathematics, specifically in abstract algebra and its applications, discrete logarithms are group-theoretic analogues of ordinary logarithms. In particular, an ordinary logarithm loga is a solution of the equation ax = b over the real or complex numbers...
problem.