Forward price
Encyclopedia
The forward price is the agreed upon price of an asset
in a forward contract
. Using the rational pricing
assumption, for a forward contract on an underlying asset that is tradeable, we can express the forward price in terms of the spot price
and any dividends etc. For forwards on non-tradeables, pricing the forward may be a complex task.
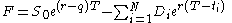
where
At the very least we know that both do not want to lose any money in the deal.
The short position knows as much as the long position knows: the short/long positions are both aware of any schemes that they could partake on to gain a profit given some forward price.
So of course they will have to settle on a fair price or else the transaction cannot occur.
An economic articulation would be:
(fair price + future value of asset's dividends) - spot price of asset = cost of capital
Forward price = Spot Price - cost of carry
The future value of that asset's dividends (this could also be coupons from bonds, monthly rent from a house, fruit from a crop, etc.) is calculated using the risk-free force of interest. This is because we are in a risk-free situation (the whole point of the forward contract is to get rid of risk or to at least reduce it) so why would the owner of the asset take any chances? He would reinvest at the risk-free rate (i.e. U.S. T-bills which are considered risk-free). The spot price of the asset is simply the market value at the instant in time when the forward contract is entered into.
So OUT - IN = NET GAIN and his net gain can only come from the opportunity cost of keeping the asset for that time period (he could have sold it and invested the money at the risk-free rate).
let:
Solving for fair price and substituting mathematics we get:
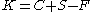
where:
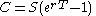
(since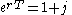
where j is the effective rate of interest per time period of T )
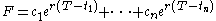
where ci is the i th dividend paid at time t i.
Doing some reduction we end up with:
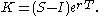
Notice that implicit in the above derivation is the assumption that the underlying can be traded. This assumption does not hold for certain kinds of forwards.
. This difference disappears when interest rates are deterministic.
In the language of stochastic processes, the forward price is a martingale
under the forward measure
, whereas the futures price is a martingale under the risk-neutral measure
. The forward measure and the risk neutral measure are the same when interest rates are deterministic.
See Musiela and Rutkowski's book on Martingale Methods in Financial Markets for a continuous time proof of this result. See van der Hoek and Elliott's book on Binomial Models in Finance for the discrete time version of this result.
Asset
In financial accounting, assets are economic resources. Anything tangible or intangible that is capable of being owned or controlled to produce value and that is held to have positive economic value is considered an asset...
in a forward contract
Forward contract
In finance, a forward contract or simply a forward is a non-standardized contract between two parties to buy or sell an asset at a specified future time at a price agreed today. This is in contrast to a spot contract, which is an agreement to buy or sell an asset today. It costs nothing to enter a...
. Using the rational pricing
Rational pricing
Rational pricing is the assumption in financial economics that asset prices will reflect the arbitrage-free price of the asset as any deviation from this price will be "arbitraged away"...
assumption, for a forward contract on an underlying asset that is tradeable, we can express the forward price in terms of the spot price
Spot price
The spot price or spot rate of a commodity, a security or a currency is the price that is quoted for immediate settlement . Spot settlement is normally one or two business days from trade date...
and any dividends etc. For forwards on non-tradeables, pricing the forward may be a complex task.
Forward Price Formula
If the underlying asset is tradeable, the forward price is given by: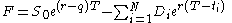where
- F is the forward price to be paid at time T
- ex is the exponential functionExponential functionIn mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
(used for calculating compounding interests) - r is the risk-free interest rateRisk-free interest rateRisk-free interest rate is the theoretical rate of return of an investment with no risk of financial loss. The risk-free rate represents the interest that an investor would expect from an absolutely risk-free investment over a given period of time....
- q is the cost-of-carry
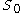is the spot priceSpot priceThe spot price or spot rate of a commodity, a security or a currency is the price that is quoted for immediate settlement . Spot settlement is normally one or two business days from trade date...
of the asset (i.e. what it would sell for at time 0)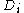
is a dividendDividendDividends are payments made by a corporation to its shareholder members. It is the portion of corporate profits paid out to stockholders. When a corporation earns a profit or surplus, that money can be put to two uses: it can either be re-invested in the business , or it can be distributed to...
which is guaranteed to be paid at tim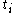e
where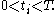 
Proof of the forward price formula
The two questions here are what price the short position (the seller of the asset) should offer to maximize his gain, and what price the long position (the buyer of the asset) should accept to maximize his gain?At the very least we know that both do not want to lose any money in the deal.
The short position knows as much as the long position knows: the short/long positions are both aware of any schemes that they could partake on to gain a profit given some forward price.
So of course they will have to settle on a fair price or else the transaction cannot occur.
An economic articulation would be:
(fair price + future value of asset's dividends) - spot price of asset = cost of capital
Forward price = Spot Price - cost of carry
The future value of that asset's dividends (this could also be coupons from bonds, monthly rent from a house, fruit from a crop, etc.) is calculated using the risk-free force of interest. This is because we are in a risk-free situation (the whole point of the forward contract is to get rid of risk or to at least reduce it) so why would the owner of the asset take any chances? He would reinvest at the risk-free rate (i.e. U.S. T-bills which are considered risk-free). The spot price of the asset is simply the market value at the instant in time when the forward contract is entered into.
So OUT - IN = NET GAIN and his net gain can only come from the opportunity cost of keeping the asset for that time period (he could have sold it and invested the money at the risk-free rate).
let:
- K = fair price
- C = cost of capital
- S = spot price of asset
- F = future value of asset's dividend
- I = present value of F (discounted using r )
- r = risk-free interest rate compounded continuously
- T = length of time from when the contract was entered into
Solving for fair price and substituting mathematics we get:
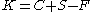
where:
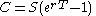
(since
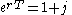where j is the effective rate of interest per time period of T )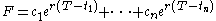where ci is the i th dividend paid at time t i.
Doing some reduction we end up with:
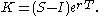
Notice that implicit in the above derivation is the assumption that the underlying can be traded. This assumption does not hold for certain kinds of forwards.
Forward versus Futures prices
There is a difference between forward and futures prices when interest rates are stochasticStochastic
Stochastic refers to systems whose behaviour is intrinsically non-deterministic. A stochastic process is one whose behavior is non-deterministic, in that a system's subsequent state is determined both by the process's predictable actions and by a random element. However, according to M. Kac and E...
. This difference disappears when interest rates are deterministic.
In the language of stochastic processes, the forward price is a martingale
Martingale (probability theory)
In probability theory, a martingale is a model of a fair game where no knowledge of past events can help to predict future winnings. In particular, a martingale is a sequence of random variables for which, at a particular time in the realized sequence, the expectation of the next value in the...
under the forward measure
Forward measure
In finance, a T-forward measure is a pricing measure absolutely continuous with respect to a risk-neutral measure but rather than using the money market as numeraire, it uses a bond with maturity T...
, whereas the futures price is a martingale under the risk-neutral measure
Risk-neutral measure
In mathematical finance, a risk-neutral measure, is a prototypical case of an equivalent martingale measure. It is heavily used in the pricing of financial derivatives due to the fundamental theorem of asset pricing, which implies that in a complete market a derivative's price is the discounted...
. The forward measure and the risk neutral measure are the same when interest rates are deterministic.
See Musiela and Rutkowski's book on Martingale Methods in Financial Markets for a continuous time proof of this result. See van der Hoek and Elliott's book on Binomial Models in Finance for the discrete time version of this result.
See also
- Forward rateForward rateThe forward rate is the future yield on a bond. It is calculated using the yield curve. For example, the yield on a three-month Treasury bill six months from now is a forward rate.-Forward rate calculation:...
- Forward measureForward measureIn finance, a T-forward measure is a pricing measure absolutely continuous with respect to a risk-neutral measure but rather than using the money market as numeraire, it uses a bond with maturity T...
- Convenience yieldConvenience yieldA convenience yield is an adjustment to the cost of carry in the non-arbitrage pricing formula for forward prices in markets with trading constraints....
- Cost of carryCost of carryThe cost of carry is the cost of "carrying" or holding a position. If long, the cost of carry is the cost of interest paid on a margin account. Conversely, if short, the cost of carry is the cost of paying dividends, or rather the opportunity cost; the cost of purchasing a particular security...
- BackwardationBackwardationNormal backwardation, also sometimes called backwardation, is the market condition wherein the price of a forward or futures contract is trading below the expected spot price at contract maturity. The resulting futures or forward curve would typically be downward sloping , since contracts for...
- ContangoContangoContango is the market condition wherein the price of a forward or futures contract is trading above the expected spot price at contract maturity. The resulting futures or forward curve would typically be upward sloping , since contracts for further dates would typically trade at even higher prices...