Four-momentum
Encyclopedia
In special relativity
, four-momentum is the generalization of the classical three-dimensional momentum
to four-dimensional spacetime
. Momentum is a vector in three dimensions; similarly four-momentum is a four-vector
in spacetime
. The contravariant four-momentum of a particle with three-momentum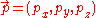
and energy 
is
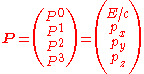
The four-momentum is useful in relativistic calculations because it is a Lorentz vector. This means that it is easy to keep track of how it transforms under Lorentz transformation
s.
(The above definition applies under the coordinate convention that
. Some authors use the convention 
which yields a modified definition with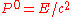 
. It is also possible to define covariant four-momentum 
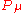where the sign of 
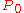is reversed.)
c) to the square of the particle's proper mass: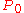
where we use the convention that
is the reciprocal of the metric tensor of special relativity
.
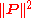is Lorentz invariant, meaning its value is not changed by Lorentz transformations/boosting into different frames of reference.
m multiplied by the particle's four-velocity
:
where the four-velocity is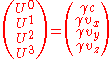
and
is the Lorentz factor
and c is the speed of light
.
Note that the invariant mass of a system of particles may be more than the sum of the particles' rest masses, since kinetic energy
in the system center-of-mass frame and potential energy
from forces between the particles contribute to the invariant mass. As an example, two particles with four-momenta (−5 GeV/c, 4 GeV/c, 0, 0) and (−5 GeV/c, −4 GeV/c, 0, 0) each have (rest) mass 3 GeV/c2 separately, but their total mass (the system mass) is 10 GeV/c2. If these particles were to collide and stick, the mass of the composite object would be 10 GeV/c2.
One practical application from particle physics
of the conservation of the invariant mass
involves combining the four-momenta P(A) and P(B) of two daughter particles produced in the decay of a heavier particle with four-momentum P(C) to find the mass of the heavier particle. Conservation of four-momentum gives P(C)μ = P(A)μ + P(B)μ, while the mass M of the heavier particle is given by -||P(C)||2 = M2c2. By measuring the energies and three-momenta of the daughter particles, one can reconstruct the invariant mass of the two-particle system, which must be equal to M. This technique is used, e.g., in experimental searches for Z' bosons at high-energy particle collider
s, where the Z' boson would show up as a bump in the invariant mass spectrum of electron
-positron
or muon
-antimuon pairs.
If an object's mass does not change, the Minkowski inner product of its four-momentum and corresponding four-acceleration
Aμ is zero. The four-acceleration is proportional to the proper time derivative of the four-momentum divided by the particle's mass, so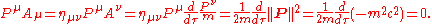
, which is the sum of the four-momentum and the product of the electric charge
with the electromagnetic four-potential
:
where the four-vector potential is a result of combining the scalar potential
and the vector potential
:
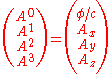
This allows the potential energy from the charged particle in an electrostatic potential and the Lorentz force
on the charged particle moving in a magnetic field to be incorporated in a compact way into the Schrödinger equation
.
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
, four-momentum is the generalization of the classical three-dimensional momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
to four-dimensional spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
. Momentum is a vector in three dimensions; similarly four-momentum is a four-vector
Four-vector
In the theory of relativity, a four-vector is a vector in a four-dimensional real vector space, called Minkowski space. It differs from a vector in that it can be transformed by Lorentz transformations. The usage of the four-vector name tacitly assumes that its components refer to a standard basis...
in spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
. The contravariant four-momentum of a particle with three-momentum
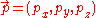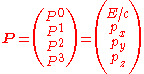
and energy isThe four-momentum is useful in relativistic calculations because it is a Lorentz vector. This means that it is easy to keep track of how it transforms under Lorentz transformation
Lorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
s.
(The above definition applies under the coordinate convention that
. Some authors use the convention which yields a modified definition with 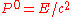. It is also possible to define covariant four-momentum 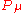where the sign of 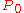is reversed.)Minkowski norm
Calculating the Minkowski norm of the four-momentum gives a Lorentz invariant quantity equal (up to factors of the speed of lightSpeed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
c) to the square of the particle's proper mass:
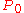
where we use the convention that
is the reciprocal of the metric tensor of special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
.
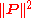is Lorentz invariant, meaning its value is not changed by Lorentz transformations/boosting into different frames of reference.Relation to four-velocity
For a massive particle, the four-momentum is given by the particle's invariant massInvariant mass
The invariant mass, rest mass, intrinsic mass, proper mass or just mass is a characteristic of the total energy and momentum of an object or a system of objects that is the same in all frames of reference related by Lorentz transformations...
m multiplied by the particle's four-velocity
Four-velocity
In physics, in particular in special relativity and general relativity, the four-velocity of an object is a four-vector that replaces classicalvelocity...
:
where the four-velocity is
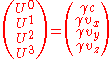
and
is the Lorentz factorLorentz factor
The Lorentz factor or Lorentz term appears in several equations in special relativity, including time dilation, length contraction, and the relativistic mass formula. Because of its ubiquity, physicists generally represent it with the shorthand symbol γ . It gets its name from its earlier...
and c is the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
.
Conservation of four-momentum
The conservation of the four-momentum yields two conservation laws for "classical" quantities:- The total energyEnergyIn physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
E = P0c is conserved. - The classical three-momentumMomentumIn classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
is conserved.
Note that the invariant mass of a system of particles may be more than the sum of the particles' rest masses, since kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
in the system center-of-mass frame and potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
from forces between the particles contribute to the invariant mass. As an example, two particles with four-momenta (−5 GeV/c, 4 GeV/c, 0, 0) and (−5 GeV/c, −4 GeV/c, 0, 0) each have (rest) mass 3 GeV/c2 separately, but their total mass (the system mass) is 10 GeV/c2. If these particles were to collide and stick, the mass of the composite object would be 10 GeV/c2.
One practical application from particle physics
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
of the conservation of the invariant mass
Invariant mass
The invariant mass, rest mass, intrinsic mass, proper mass or just mass is a characteristic of the total energy and momentum of an object or a system of objects that is the same in all frames of reference related by Lorentz transformations...
involves combining the four-momenta P(A) and P(B) of two daughter particles produced in the decay of a heavier particle with four-momentum P(C) to find the mass of the heavier particle. Conservation of four-momentum gives P(C)μ = P(A)μ + P(B)μ, while the mass M of the heavier particle is given by -||P(C)||2 = M2c2. By measuring the energies and three-momenta of the daughter particles, one can reconstruct the invariant mass of the two-particle system, which must be equal to M. This technique is used, e.g., in experimental searches for Z' bosons at high-energy particle collider
Collider
A collider is a type of a particle accelerator involving directed beams of particles.Colliders may either be ring accelerators or linear accelerators.-Explanation:...
s, where the Z' boson would show up as a bump in the invariant mass spectrum of electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
-positron
Positron
The positron or antielectron is the antiparticle or the antimatter counterpart of the electron. The positron has an electric charge of +1e, a spin of ½, and has the same mass as an electron...
or muon
Muon
The muon |mu]] used to represent it) is an elementary particle similar to the electron, with a unitary negative electric charge and a spin of ½. Together with the electron, the tau, and the three neutrinos, it is classified as a lepton...
-antimuon pairs.
If an object's mass does not change, the Minkowski inner product of its four-momentum and corresponding four-acceleration
Four-acceleration
In special relativity, four-acceleration is a four-vector and is defined as the change in four-velocity over the particle's proper time:whereandand \gamma_u is the Lorentz factor for the speed u...
Aμ is zero. The four-acceleration is proportional to the proper time derivative of the four-momentum divided by the particle's mass, so
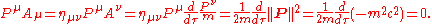
Canonical momentum in the presence of an electromagnetic potential
For applications in relativistic quantum mechanics, it is useful to define a "canonical" momentum four-vector,, which is the sum of the four-momentum and the product of the electric chargeElectric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
with the electromagnetic four-potential
Electromagnetic four-potential
The electromagnetic four-potential is a potential from which the electromagnetic field can be derived. It combines both the electric scalar potential and the magnetic vector potential into a single space-time four-vector. In a given reference frame, the first component is the scalar potential and...
:
where the four-vector potential is a result of combining the scalar potential
Scalar potential
A scalar potential is a fundamental concept in vector analysis and physics . The scalar potential is an example of a scalar field...
and the vector potential
Vector potential
In vector calculus, a vector potential is a vector field whose curl is a given vector field. This is analogous to a scalar potential, which is a scalar field whose negative gradient is a given vector field....
:
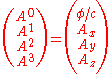
This allows the potential energy from the charged particle in an electrostatic potential and the Lorentz force
Lorentz force
In physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
on the charged particle moving in a magnetic field to be incorporated in a compact way into the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
.