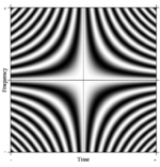
Fourier operator
Encyclopedia
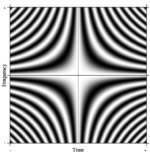
Continuous Fourier transform
The Fourier transform is a mathematical operation that decomposes a function into its constituent frequencies, known as a frequency spectrum. For instance, the transform of a musical chord made up of pure notes is a mathematical representation of the amplitudes of the individual notes that make...
.
It may be thought of as a limiting case for when the size of the discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
increases without bound while its spatial resolution also increases without bound, so as to become both continuous and not necessarily periodic.
As a teaching tool the Fourier operator is used widely and it has also been used as an art form, including the book cover of the book entitled Advances in Machine Vision ISBN 9810209762.
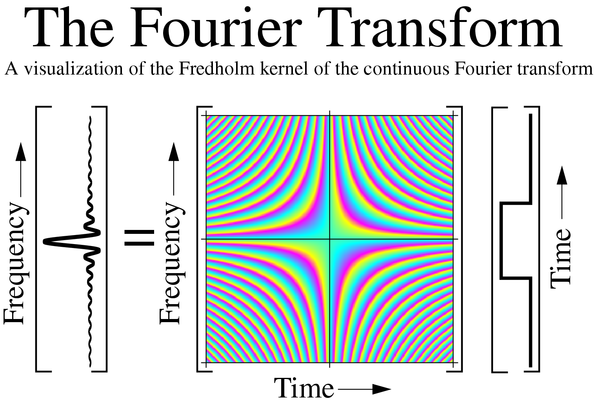
Visualization of the Fourier transform as the result of the Fourier operator
The Fourier operator defines a continuous two-dimensional function that extends along time and frequency axes, outwards to infinity in all four directions. This is analogous to the DFT matrixDFT matrix
A DFT matrix is an expression of a discrete Fourier transform as a matrix multiplication.-Definition:An N-point DFT is expressed as an N-by-N matrix multiplication as X = W x, where x is the original input signal, and X is the DFT of the signal.The transformation W of size N\times N can be defined...
but, in this case, is continuous and infinite in extent. The value of the function at any point is such that it has the same magnitude everywhere. Along any fixed value of time, the value of the function varies as a complex exponential in frequency. Likewise along any fixed value of frequency the value of the function varies as a complex exponential in time. A portion of the infinite Fourier operator is shown in the illustration below, which depicts how it acts on a rectangular pulse to generate its Fourier transform (in this case, a sinc function):
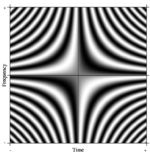
Any slice parallel to either of the axes, through the Fourier operator, is a complex exponential, i.e. the real part is a cosine wave and the imaginary part is a sine wave of the same frequency as the real part.
Diagonal slices through the Fourier operator give rise to chirps. Thus rotation of the Fourier operator gives rise to the fractional Fourier transform
Fractional Fourier transform
In mathematics, in the area of harmonic analysis, the fractional Fourier transform is a linear transformation generalizing the Fourier transform. It can be thought of as the Fourier transform to the n-th power where n need not be an integer — thus, it can transform a function to an...
, which is related to the chirplet transform
Chirplet transform
In signal processing, the chirplet transform is an inner product of an input signal with a family of analysis primitives called chirplets.-Similarity to other transforms:...
.

