
Fractional order integrator
Encyclopedia
A fractional order integrator or just simply fractional integrator is an integrator
device that calculates the fractional order integral or derivative (usually called a differintegral) of an input. Differentiation or integration is a real or complex parameter. The fractional integrator is useful in fractional order control
where the history of the system under control is important to the control system output.
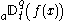
includes the integer order differentiation and integration functions, and allows a continuous range of functions around them. The differintegral parameters are a, t, and q. The parameters a and t describe the range over which to compute the result. The differintegral parameter q may be any real number or complex number. If q is greater than zero, the differintegral computes a derivative. If q is less than zero, the differintegral computes an integral.
The integer order integration can be computed as a Riemann-Liouville differintegral, where the weight of each element in the sum is the constant unit value 1, which is equivalent to the Riemann sum
. To compute an integer order derivative, the weights in the summation would be zero, with the exception of the most recent data points, where (in the case of the first unit derivative) the weight of the data point at t−1 is −1 and the weight of the data point at t is 1. The sum of the points in the input function using these weights results in the difference of the most recent data points.
These weights are computed using ratios of the Gamma function
incorporating the number of data points in the range [a,t], and the parameter q.
A solution to this problem is the Coopmans Approximation
, which allows old data to be forgotten more gracefully (though still with exponential decay, rather than with the power law decay of a purely analog device
).
There is no error due to round-off
, as in the case of digital devices, but there may be error in the device due to leakage
s, and also unexpected variations in behavior caused by heat and noise.
An example fractional order integrator is a modification of the standard integrator circuit, where a capacitor
is used as the feedback impedance on an opamp. By replacing the capacitor with an RC Ladder circuit, a half order integrator, that is, with

can be constructed.
Integrator
An integrator is a device to perform the mathematical operation known as integration, a fundamental operation in calculus.The integration function is often part of engineering, physics, mechanical, chemical and scientific calculations....
device that calculates the fractional order integral or derivative (usually called a differintegral) of an input. Differentiation or integration is a real or complex parameter. The fractional integrator is useful in fractional order control
Fractional order control
Fractional order control or is a field of control theory that uses the fractional order integrator as part of the control system design toolkit....
where the history of the system under control is important to the control system output.
Overview
The differintegral function,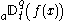
includes the integer order differentiation and integration functions, and allows a continuous range of functions around them. The differintegral parameters are a, t, and q. The parameters a and t describe the range over which to compute the result. The differintegral parameter q may be any real number or complex number. If q is greater than zero, the differintegral computes a derivative. If q is less than zero, the differintegral computes an integral.
The integer order integration can be computed as a Riemann-Liouville differintegral, where the weight of each element in the sum is the constant unit value 1, which is equivalent to the Riemann sum
Riemann sum
In mathematics, a Riemann sum is a method for approximating the total area underneath a curve on a graph, otherwise known as an integral. It mayalso be used to define the integration operation. The method was named after German mathematician Bernhard Riemann....
. To compute an integer order derivative, the weights in the summation would be zero, with the exception of the most recent data points, where (in the case of the first unit derivative) the weight of the data point at t−1 is −1 and the weight of the data point at t is 1. The sum of the points in the input function using these weights results in the difference of the most recent data points.
These weights are computed using ratios of the Gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
incorporating the number of data points in the range [a,t], and the parameter q.
Digital devices
Digital devices have the advantage of being versatile, and are not susceptible to unexpected output variation due to heat or noise. The discrete nature of a computer however, does not allow for all of history to be computed. Some finite range [a,t] must exist. Therefore, the number of data points that can be stored in memory ( N ), determines the oldest data point in memory, so that the value a is never more than N samples old. The effect is that any history older than a is completely forgotten, and no longer influences the output.A solution to this problem is the Coopmans Approximation
Coopmans Approximation
The Coopmans Approximation is a method for approximating a fractional order integrator in a continuous process with constant space complexity...
, which allows old data to be forgotten more gracefully (though still with exponential decay, rather than with the power law decay of a purely analog device
Analog device
Analog device is an apparatus that measures continuous information. The measured analog signal has an infinite number of possible values. The only limitation on resolution is the accuracy of the measuring device. Such apparatus operates with variables which are constituted by continuously measured...
).
Analog devices
Analog devices have the ability to retain history over longer intervals. This translates into the parameter a staying constant, while t increases.There is no error due to round-off
Round-off error
A round-off error, also called rounding error, is the difference between the calculated approximation of a number and its exact mathematical value. Numerical analysis specifically tries to estimate this error when using approximation equations and/or algorithms, especially when using finitely many...
, as in the case of digital devices, but there may be error in the device due to leakage
Leakage
Leakage may refer to:*Leakage *Memory leak, in computer science*Leakage *Leakage *Leakage *Leakage...
s, and also unexpected variations in behavior caused by heat and noise.
An example fractional order integrator is a modification of the standard integrator circuit, where a capacitor
Capacitor
A capacitor is a passive two-terminal electrical component used to store energy in an electric field. The forms of practical capacitors vary widely, but all contain at least two electrical conductors separated by a dielectric ; for example, one common construction consists of metal foils separated...
is used as the feedback impedance on an opamp. By replacing the capacitor with an RC Ladder circuit, a half order integrator, that is, with

can be constructed.

